线性回归---Fit A Line

最近在上【开课吧人工智能学院】，第六期【计算机视觉】的课程。讲师上课讲了线性回归与逻辑回归。我来简单总结一下线性回归～
那就从我有一个房子开始吧～ 最近想去大城市闯荡，需要钱，想卖掉老家的房子。我知道自己的房子150平米，我想预估这个房子的价格。我就去卖房子的网站去看别人的房子都是什么样的价格。刚开始我很单纯，只关注了一个点，就是房子的面积和价格。
我收集了以下数据：（100平米，350万）（200平米，650万），就想自己的房子应该介于350万到650万之间。

我是学习过数学嘛，想到 $y=ax+b$ ,根据两个数据的规律得到以下经验：

房子价格 = 3 ✖️房子的面积 + 50。

那我把自己房子的面积带入，那价格应该是500万。

以上过程，进一步理解。

• 关于收集来的简单数据可看作数据集，简单记为（$x$ ,$y$）。
• 房子的面积可看作特征。
• 线性方程中的 $a$、$b$ 可看作参数，根据数据求得 $a$、$b$，可看作求参数的过程，也可称作训练过程。训练所用的数据又是训练集。
• 房子的价格能影响参数的值，这样的影响，可看作有监督的过程，房子的价格监督 $a$、$b$ 求解的过程。
• 函数【房子价格 = 3 ✖️房子的面积 + 50】 可看作一个模型，带入新的数据【房子的面积】可知道该房子的价格。

那我继续收集数据～

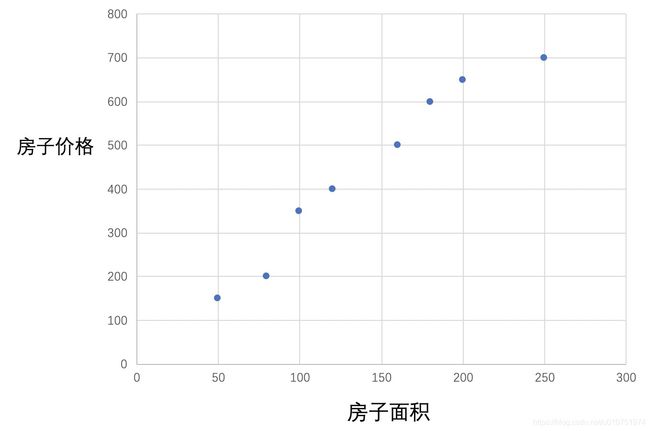
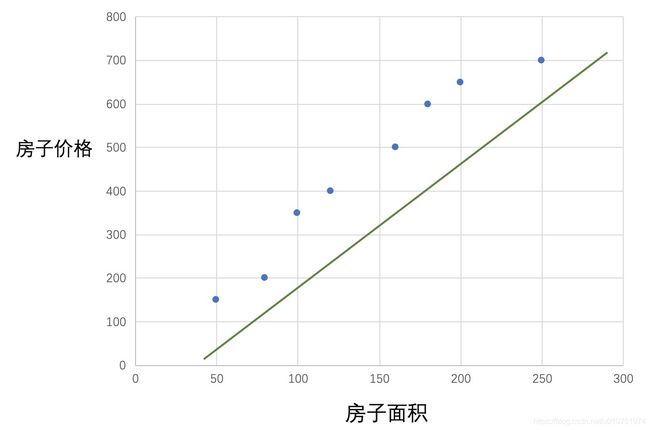
现在继续使用一条直线去靠近这些点，便以下的图示过程，可称作拟合的过程。

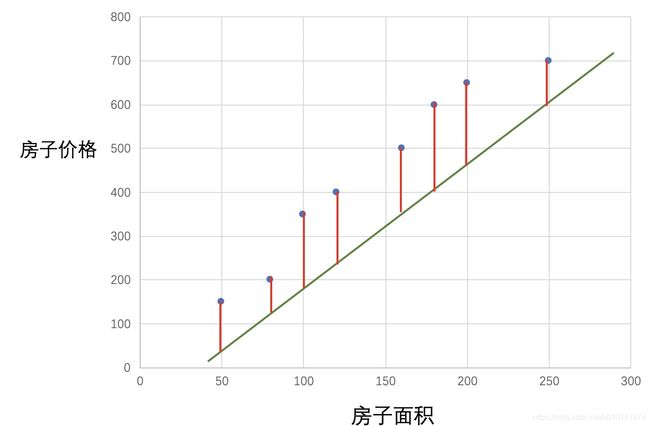
用红色的线记录同一个横轴下直线与点的差异。


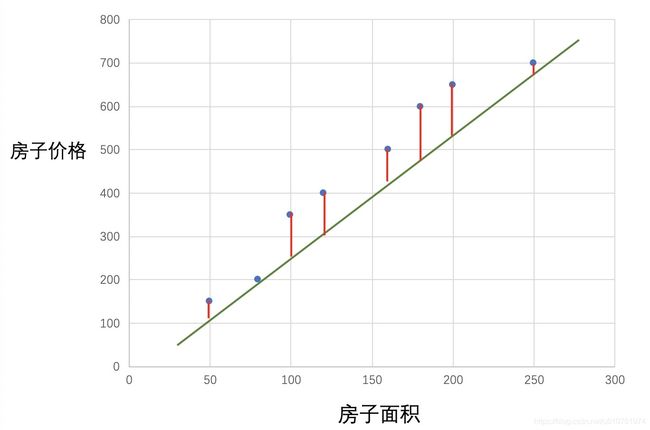
可以看到，当所有红色的线累计到最短的时候，便是拟合效果最好的时候。
我们将绿色直线的值记为 $\hat{y}$。那 $|\hat{y}-y|$ 表示拟合直线与真实值的误差(Error)，即是红色的线。则所有数据的平均绝对误差（Mean Absolute Error，MAE），若有$m$个数据，第$i$个数据下的真实值表示为$y^i$，拟合曲线在第个值下的值为 ${\hat{y}}^i$, MAE表示为：
$$MAE=\frac{1}{m}\sum _{i=1}^m|{\hat{y}}^i-y^i|$$
同样，考虑到拟合直线与真实值的面积误差，称之为 Mean Squared Error（MSE），表达式如下：
$$MSE=\frac{1}{2m}\sum _{i=1}^m({\hat{y}}^i-y^i{)}^2$$
这样，我们的目标是希望拟合直线与真实值的误差最小，可以选择MSE或者MAE，监督参数的求解,这样的MSE/MAE的函数，又称为损失函数/期望函数/目标函数(cost/loss/target function)。

== 那如何求解参数呢？==
选择MSE作为监督的函数 ，cost function = MSE 。
目标是希望 MSE 越小越好，如何让MSE越来越小呢？也就是随机调整参数 $a$、$b$。通过观察 cost function的值，监督参数 $a$、$b$ 的调整。
随机调整参数有点佛系，比较耗时。
有没有谁能指点方向，让参数求解faster呢？
梯度的方向是函数变化最快的方向。梯度便可用于参数求解。CV讲师给出了如何求参数的过程。
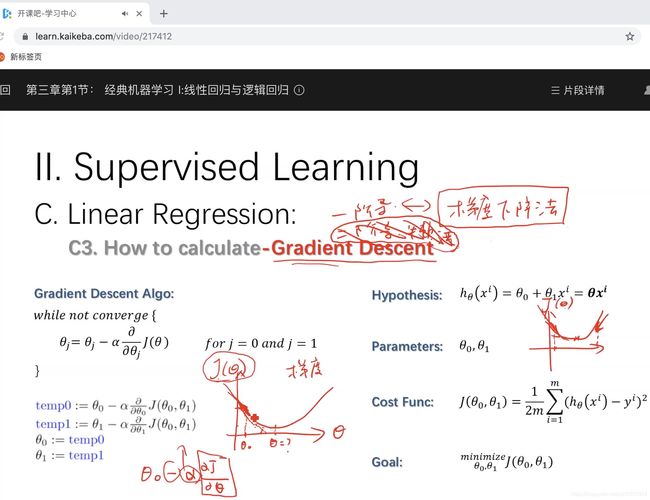那我照葫芦画瓢～

• Hypothesis (拟合的直线) ： $y=ax+b$

• Parameters (参数) ： $a,b$

• Cost Func (损失函数) ： $Cost(a,b)=\frac{1}{2m}{\sum }_{i=1}^m({\hat{y}}^i-y^i{)}^2$

• Goal ：${\min }_{a,b}Cost(a,b)$

梯度下降

• 首先对 $a$、$b$ 赋值，这个值可以是随机的，也可以是一个零向量；
• 改变 $a$、$b$ 的值，使得 $Cost(a,b)$ 按梯度下降的方向进行减少；
• 当 $Cost(a,b)$ 下降到无法下降时为止，这时 $Cost(a,b)$ 对 $a,b$ 的导数为0.

以上的参数是怎么改变的呢？
$$temp0=a-\lambda \frac{\partial }{\partial a}Cost(a,b)$$

$$temp1=b-\lambda \frac{\partial }{\partial b}Cost(a,b)$$

$$a:=temp0$$

$$a:=temp1$$

$\lambda$ 是步长，也被成为学习率，凭经验值。

$\frac{\partial }{\partial a}Cost(a,b)$，$\frac{\partial }{\partial b}Cost(a,b)$ 是多少呢？
$$\frac{\partial }{\partial a}Cost(a,b)=\frac{1}{m}\sum _{i=1}^m({\hat{y}}^i-y^i)x$$
$$\frac{\partial }{\partial b}Cost(a,b)=\frac{1}{m}\sum _{i=1}^m({\hat{y}}^i-y^i)$$

参数求解之后，带入拟合的直线，拟合的直线可以对新的数据进行预测。现在进入代码实践的过程～

# inference 拟合的直线 y_hat
def inference(a,b,x):
    y_hat = a * x + b
    return y_hat
    
# cost function
def eval_loss(a,b,x_list,gt_y_list):
    avg_loss = 0
    for i in range(len(x_list)):
        avg_loss += 0.5 * (a * x_list[i] + b - gt_y_list[i]) ** 2
    avg_loss /= len(gt_y_list)
    return avg_loss
# 一个数据的梯度
def gradient(y_hat, gt_y, x):
    diff = y_hat - gt_y
    da = diff * x
    db = diff
    return da,db
    
def cal_step_gradient(x_list, gt_y_list, a, b ,lr):
    avg_da, avg_db = 0, 0
    x_number = len(x_list)
    for i in range( len(x_list)):
        y_hat = inference(a, b, x_list[i])
        da, db = gradient(y_hat, gt_y_list[i], x_list[i])
        avg_da += da
        avg_db += db
    avg_da /= x_number
    avg_db /= x_number
    a -= lr * avg_da
    b -= lr * avg_db
    return a,b
    
def train(x_list, gt_y_list, lr, max_iter):
    a = 0
    b = 0
    num_samples = len(x_list)
    for i in range(max_iter): 
        a, b = cal_step_gradient(x_list, gt_y_list, a, b, lr)
        print('a:{0},b:{1}'.format(a,b))
        print('loss is {}'.format(eval_loss(a,b,x_list,gt_y_list)))
        time.sleep(0.1)
    return a,b

import time
import pandas as pd 
import matplotlib.pyplot as plt
%matplotlib inline

data = pd.DataFrame({'size': [50, 80, 100, 120, 160, 180, 200, 250],
                     'price': [150, 200, 350, 400, 500, 600, 650, 700]})
train(data['size'], data['price'],0.1, 4)

我做的这份笔记只是课堂内容的冰山一角，我要继续啃冰山了。。。