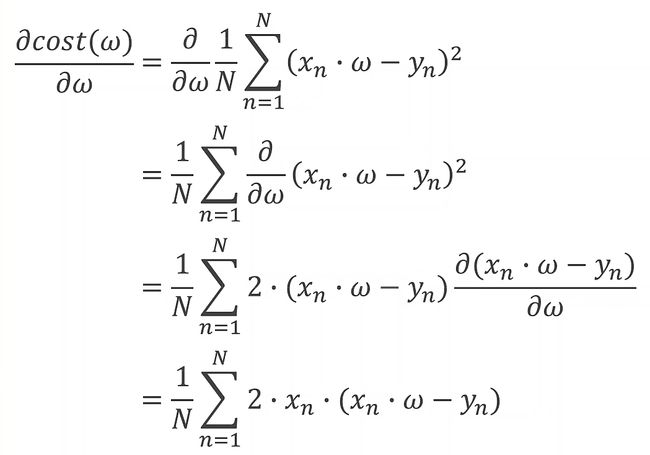线性模型（梯度下降&随机梯度下降）

参考视频：03.梯度下降算法_哔哩哔哩_bilibili

显然使用穷举法效率太低了，如果权重多一些，时间复杂度将是指数级的增长。所以我们需要使用梯度下降算法来优化。

梯度Gradient：$$\frac{\partial cost}{\partial w}$$

用梯度来更新权重w：

$$w=w-\alpha \frac{\partial cost}{\partial w}$$

（如果梯度大于0，则表示当前方向是误差增大的方向，需要往方向更新w；反之，如果梯度小于0，则表示沿当前方向是误差减小）

1 梯度下降算法

参考视频中$$y=wx$$的样例，我们尝试一下$$y=wx+b$$

还是以$$y=3x+2$$为例（事先不知道）

学习率设为0.01，训练2000次

代码如下：

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]

w = 2.0
b = 1.0
lr = 0.01


def forward(x):
    return w * x + b


# 计算误差
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs, ys):
        y_pred = forward(x)
        cost += (y_pred - y) ** 2
    return cost / len(xs)


# 计算w的梯度
def gradient_w(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * x * (x * w + b - y)
    return grad / len(xs)


# 计算b的梯度
def gradient_b(xs, ys):
    grad = 0
    for x, y in zip(xs, ys):
        grad += 2 * (x * w + b - y)
    return grad / len(xs)


shuffle_array = [0, 1, 2]
cost_list = []

for epoch in range(2000):   # 训练2000次
    cost_val = cost(x_data, y_data)
    grad_w_val = gradient_w(x_data, y_data)
    grad_b_val = gradient_b(x_data, y_data)
    w -= lr * grad_w_val    # 更新w
    b -= lr * grad_b_val    # 更新b

    print('Epoch:', epoch, 'w=', w, ' b=', b, ' loss=', cost_val)
    # print('gw:', grad_w_val, 'gb:', grad_b_val)
    cost_list.append(cost_val)
print('Predict(after training', 4, forward(4))

plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Cost')
plt.plot(np.arange(0, 2000, 1), np.array(cost_list))
plt.show()

2000次训练后结果如下，很逼近我们的答案w=3，b=2

2 随机梯度下降

用随机梯度下降的思想进一步优化，学习率调整为0.05，训练次数调整为100次（实际为更新300次）

和上面不同的主要是，每一次从训练集中不放回地抽取一组(x,y)计算梯度，更新我们的权重w和偏置b

我们可以定义一个shuffle数组存数据索引，每个epoch开始前打乱数组顺序，再根据打乱的索引取数据

shuffle_array = [0,1,2]
random.shuffle(shuffle_array) # 打乱顺序

完整代码如下：

import numpy as np
import matplotlib.pyplot as plt
import random

x_data = [1.0, 2.0, 3.0]
y_data = [5.0, 8.0, 11.0]

w = 2.0
b = 1.0
lr = 0.05


def forward(x):
    return w * x + b


def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2


def gradient_w(x, y):
    return 2 * x * (x * w + b - y)


def gradient_b(x, y):
    return 2 * (x * w + b - y)

shuffle_array = [0,1,2]
cost_list = []

for epoch in range(100):
    random.shuffle(shuffle_array)
    print(shuffle_array)
    for i in shuffle_array:
        x, y = x_data[i], y_data[i]
        cost_val = loss(x, y)
        grad_w_val = gradient_w(x, y)
        grad_b_val = gradient_b(x, y)
        w -= lr * grad_w_val
        b -= lr * grad_b_val

    print('Epoch:', epoch, 'w=', w, ' b=', b, ' loss=', cost_val)
    cost_list.append(cost_val)
print('Predict(after training', 4, forward(4))

plt.figure()
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.plot(np.arange(0, 100, 1), np.array(cost_list))
plt.show()

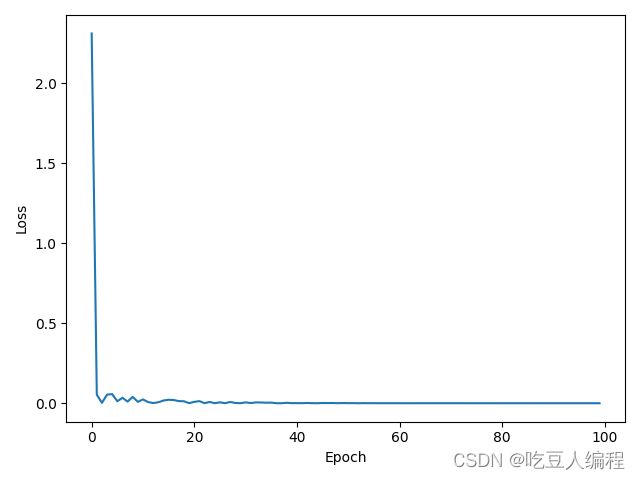
可以发现在进一步优化后，我们只用了300次的训练就达到了预期的效果