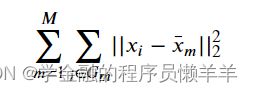【机器学习】聚类之K-means和DBSCAN

聚类分析是一种无监督学习法，它将数据点分离成若干个特定的群或组，使得在某种意义上同一组中的数据点具有相似的性质，不同组中的数据点具有不同的性质。

聚类分析包括基于不同距离度量的多种不同方法。例如。K均值（点之间的距离）、Affinity propagation（图之间的距离）、均值漂移（点之间的距离）、DBSCAN（最近点之间的距离）、高斯混合（到中心的马氏距离）、谱聚类（图之间距离）等。

所有聚类法都使用相同的方法，即首先计算相似度，然后使用相似度将数据点聚类为组或群。

1 K-means

1.1 K-means聚类简介

K-means聚类是非常常用的聚类方法之一，该方法将所有样本进行划分，使得每个样本到其类中心的平方和最小。如果我们希望分为M类，那么，记¯x¯m为第m类的中心，那么那么损失函数定义为：

算法的目的是最小化以上目标函数，那么就需要确定每一个i所属的组。然而，每个样本所属组有很多情况，这个情况数是指数级别的，实际上解以上最优化问题是一个NP-hard问题。

现实中在求解以上问题时，会先从一个简单的划分开始，通过迭代的方法直到收敛，我们在此不详细介绍算法的具体步骤。Scikit-Learn中已经有该算法的实现

K-means是一个无监督聚类的算法，也就是它根据数据本身的属性来将数据划分成不同的类别（而不是根据给定的标签）。

K-means是一个相对来说比较容易理解的算法。它每次都会根据数据的分布去寻找聚类中心。每一个点都被划分为不同的分类，每一个点与自己类别的中心在距离上都是最近的。

KMeans并不能保证最后的结果一定是收敛的。所以，scikit-learn初始化了很多随机值，去寻找最优的结果。

同时，需要进行的分类类别个数必须事先确定。对于一些其他的聚类算法，类别的个数可以事先确定。

K-Means的局限性：

• 当聚类的大小、密度、形状不同时，K-means 聚类的结果不理想
• 数据集包含离群点时，K-means 聚类结果不理想
• 两个类距离较近时，聚类结果不合理
• 在簇的平均值被定义的情况下才能使用，这对于处理符号属性的数据不适用。
• 必须事先给出k（要生成的簇的数目），而且对初值敏感，对于不同的初始值，可能会导致不同结果。经常发生得到次优划分的情况。解决方法是多次尝试不同的初始值。
• 它对于“躁声”和孤立点数据是敏感的，少量的该类数据能够对平均值产生极大的影响。

1.2 Kmeans Python 例子

导入使用的包：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import pandas as pd
import seaborn as sns; sns.set()

人为创造一个拥有8个簇的数据集并展示 

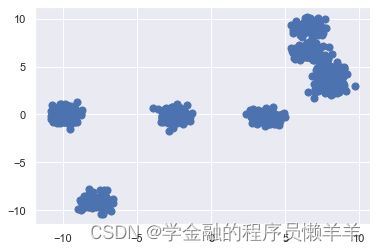
#人为创造一个拥有8个簇的数据集并展示
from sklearn.datasets import make_blobs
X, y = make_blobs(n_samples=1000, centers=8,random_state=2022, cluster_std=0.5)
plt.scatter(X[:, 0], X[:, 1], s=50);

 使用sklearn的kmeans进行聚类：

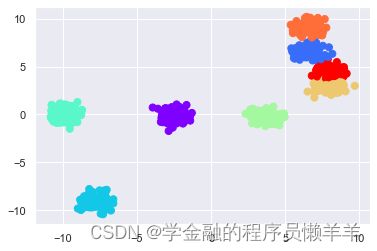
from sklearn.cluster import KMean
est = KMeans(8)   # 指定要聚类的个数
est.fit(X)         # 训练
y_kmeans = est.predict(X)   # 预测
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=50, cmap='rainbow');

 1.3 使用肘部法则确定聚类的簇的数量，使用轮廓系数判断聚类效果

在分析实际问题时，我们通常不能通过肉眼观察就清楚地知道要将数据聚成多少个类，因此我们需要有一些方法来帮助我们判断。      

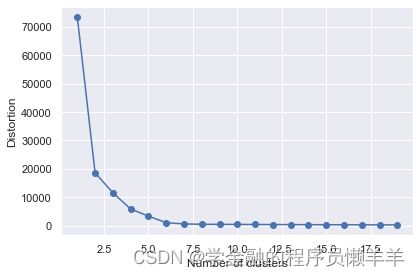
 肘部法则–Elbow Method。我们知道k-means是以最小化样本与质点平方误差作为目标函数，将每个簇的质点与簇内样本点的平方距离误差和称为畸变程度(distortions)，那么，对于一个簇，它的畸变程度越低，代表簇内成员越紧密，畸变程度越高，代表簇内结构越松散。 畸变程度会随着类别的增加而降低，但对于有一定区分度的数据，在达到某个临界点时畸变程度会得到极大改善，之后缓慢下降，这个临界点就可以考虑为聚类性能较好的点。

distortions是K-Means模型对象的属性，它作为没有真实分类结果标签下的非监督式评估指标。
表示样本到最近的聚类中心的距离总和。值越小越好，越小表示样本在类间的分布越集中。

distortions = []
for i in range(1, 20):
    km = KMeans(n_clusters=i, 
                init='k-means++', 
                n_init=10, 
                max_iter=300, 
                random_state=0)
    km.fit(X)
    distortions.append(km.inertia_) 
plt.plot(range(1,20), distortions, marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Distortion')
plt.tight_layout()
plt.show()

 

 

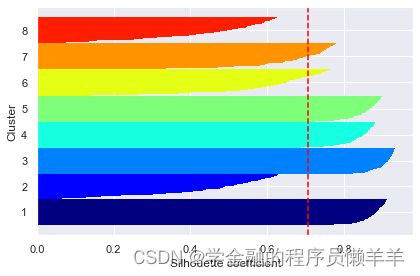
轮廓系数–Silhouette Coefficient对于一个聚类任务，我们希望得到的簇中，簇内尽量紧密，簇间尽量远离，轮廓系数便是类的密集与分散程度的评价指标，公式表达如下： s=b−amax(a,b)s=b−amax(a,b) 其中a代表同簇样本到彼此间距离的均值，b代表样本到除自身所在簇外的最近簇的样本的均值，s取值在[-1, 1]之间。 如果s接近1，代表样本所在簇合理，若s接近-1代表s更应该分到其他簇中。判断： 轮廓系数范围在[-1,1]之间。该值越大，越合理。 si接近1，则说明样本i聚类合理； si接近-1，则说明样本i更应该分类到另外的簇； 若si 近似为0，则说明样本i在两个簇的边界上。 所有样本的s i 的均值称为聚类结果的轮廓系数，是该聚类是否合理、有效的度量。 使用轮廓系数(silhouette coefficient)来确定，选择使系数较大所对应的k值。

import numpy as np
from matplotlib import cm
from sklearn.metrics import silhouette_samples
km = KMeans(n_clusters=8,    
            init='k-means++', 
            n_init=10, 
            max_iter=300,
            tol=1e-04,
            random_state=0)
y_km = km.fit_predict(X)
cluster_labels = np.unique(y_km)
n_clusters = cluster_labels.shape[0]
silhouette_vals = silhouette_samples(X, y_km, metric='euclidean')
y_ax_lower, y_ax_upper = 0, 0
yticks = []
for i, c in enumerate(cluster_labels):
    c_silhouette_vals = silhouette_vals[y_km == c]
    c_silhouette_vals.sort()
    y_ax_upper += len(c_silhouette_vals)
    color = cm.jet(float(i) / n_clusters)
    plt.barh(range(y_ax_lower, y_ax_upper), c_silhouette_vals, height=1.0, 
             edgecolor='none', color=color)

    yticks.append((y_ax_lower + y_ax_upper) / 2.)
    y_ax_lower += len(c_silhouette_vals)
   
silhouette_avg = np.mean(silhouette_vals)
plt.axvline(silhouette_avg, color="red", linestyle="--") 
plt.yticks(yticks, cluster_labels + 1)
plt.ylabel('Cluster')
plt.xlabel('Silhouette coefficient')
plt.tight_layout()
plt.show()

 

2 DBSCAN

2.1 DBSCAN简介

具有噪声的基于密度的聚类方法（DBSCAN Density-Based Spatial Clustering of Applications with Noise）。

既然已经有了K均值聚类，为什么还需要DBSCAN这样的基于密度的聚类算法呢？

K均值聚类可以将松散相关的观测聚类在一起。每一个观测最终都成为某个聚类的一部分，即使这些观测在向量空间中分散得很远。由于聚类依赖于聚类元素的均值，因此每个数据点在形成聚类中都起着作用。

数据点的轻微变化可能会影响聚类结果。由于聚类的形成方式，这个问题在DBSCAN中大大减少。这通常不是什么大问题，除非遇到一些具有古怪形状的数据。

使用K均值的另一个困难是需要指定聚类的数量（“k”）以便使用。很多时候不会预先知道什么是合理的k值。

DBSCAN的优点在于，不必指定使用它的聚类数量。需要的只是一个计算值之间距离的函数，以及一些将某些距离界定为“接近”的指令。在各种不同的分布中，DBSCAN也比K均值产生更合理的结果。

具有噪声的基于密度的聚类方法(DBSCAN)是基于密度聚类的一种基本算法。它可以从大量的数据中发现不同形状和大小的聚类，这些聚类中正包含着噪声和异常值。

DBSCAN算法使用以下两种参数：

· eps (ε)：一种距离度量，用于定位任何点的邻域内的点。

· minPts：聚类在一起的点的最小数目（一个阈值），使一个区域界定为密集。

如果探究两个称为密度可达性（DensityReachability）和密度连接性（DensityConnectivity）的概念，就可以理解这些参数。

密度方面的可达性（Reachability）建立了一个可以到达另一个点的点，如果该点位于与另一个点的特定距离（eps）内。

连接性（Connectivity）涉及到基于传递性的链接方法，以确定点是否位于特定的聚类中。例如，如果p->r->s->t->q，则p和q可以连接，其中a->b表示b在a的邻域内。

DBSCAN聚类完成后会产生三种类型的点：

· 核心点（Core）——该点表示至少有m个点在距离n的范围内。

· 边界点（Border） ——该点表示在距离n处至少有一个核心。

· 噪声点（Noise） ——它既不是核心点也不是边界点。并且它在距离自身n的范围内有不到m个点。

DBSCAN聚类算法步骤

1. 算法通过任意选取数据集中的一个点（直到所有的点都访问到）来运行。

2. 如果在该点的“ε”半径范围内至少存在“minPoint”点，那么认为所有这些点都属于同一个聚类。

3. 通过递归地重复对每个相邻点的邻域计算来扩展聚类

 2.2 DBSCAN Python 实现例子

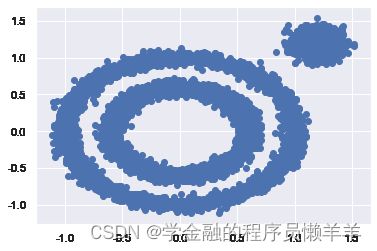
人为生成数据：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
%matplotlib inline
X1, y1=datasets.make_circles(n_samples=5000, factor=.6, noise=.05)
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]],cluster_std=[[.1]],random_state=9)
X = np.concatenate((X1, X2))
plt.scatter(X[:, 0], X[:, 1], marker='o')
plt.show()

 进行聚类：

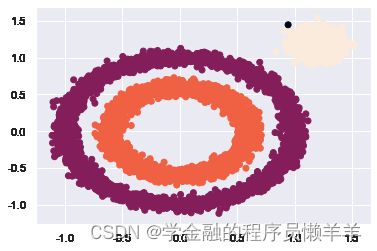
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X) 
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()

 

 注：DBSCAN的两个关键的参数eps和min_samples进行调参基本只能依靠经验进行，或使用枚举法。调参小技巧-DBSCAN参数选取方法 - 灰信网（软件开发博客聚合）