数据挖掘（一）---- PageRank算法 +缺失值补充

一 原理介绍

1.1 简介

PageRank（网页级别）用来衡量一个网站的好坏的唯一标准 ，在加入了诸如Title标识和KeyWords标识等所有其他因素后，在搜索结果中因网站排名获得提升，从而提高搜索结果的相关性和质量
其算法的核心如下：

1. 如果一个网页被很多其他网页链接连接到的话，说明这个网页比较重要，它的PageRank值会相对较高
2. 如果一个PageRank高的网站指向另一个网站，这个被指向的网站的PageRank值也会相应提高，即一个网站的PageRank值会受到其他网址的影响

示意图：

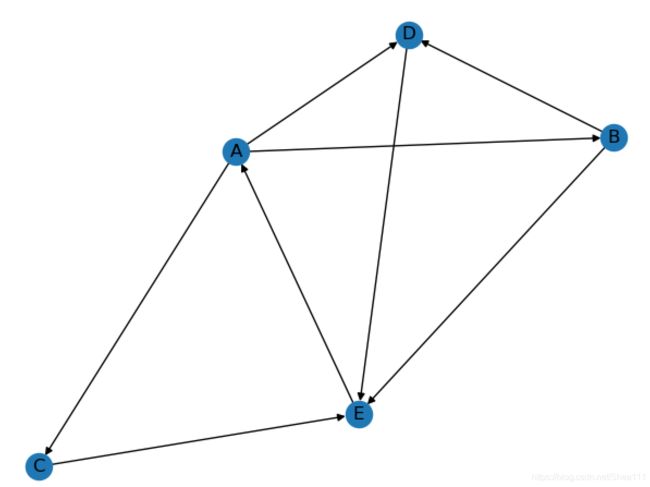
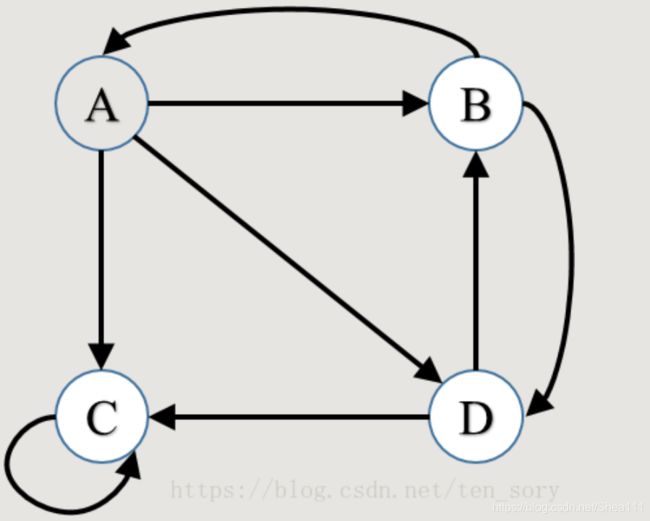
• In： 每个球代表一个网页，球的大小反应了网页的pagerank值的大小
• Out： 指向网页B和网页E的链接有很多，所以B和E的值会比较高；而C很少有网页指向它，但是因为B（重要）指向它，所以它的值也相应会提高

1.2 PageRank算法原理

参考于：PageRank算法实现

1.2.1 简单的PageRank算法

假设网页X的排名用PR(X)表示，则A的排名为PR(A)，通过这个图可以知道，B和C都指向了A，所以A的排名为
$$PR(A)=PR(C)+PR(B)$$
又因为C只指向了A，B不仅指向了A还指向了D，所以上面的公式更合理的应该是：
$$PR(A)=\frac{PR(B)}{2}+\frac{PR(C)}{1}$$

1.2.2 考虑没有出边（outlink）的算法

有的网页，会哪一个网页都不指向，那么它的值会被均分到所有的网页，即

$$PR(A)=\frac{PR(B)}{2}+\frac{PR(C)}{4}$$

1.2.3 网页链接中存在环

存在环则说明它指向的是自己，这个是可能的，因为有可能在点击网络跳转的时候转来转去都是那几个网站

所以假设当一个用户，遇上这种情况，他会以某一个概率$\alpha$随机指向任意一个网页，指向每个网页的概率相等，这个时候网页A的PageRank值可以表示为：
$$PR(A)=\alpha (\frac{PR(B)}{2})+\frac{(1-\alpha )}{4}$$
这个公式可以解释为：$\alpha$表示用户从网页B以概率$\alpha$链接到网页A，而后面的（1-$1-\alpha$）表示用户从网页C以概率$(1-\alpha )$链接到网页A
即：
网页B的Pagerank值分配情况为：$\frac{1}{2}\alpha$给A, $\frac{1}{2}\alpha$给D，$\frac{(1-\alpha )}{4}$分给其他4个网页
网页C的Pagerank值分配情况为：$\alpha$给自己（C），$\frac{(1-\alpha )}{4}$分给其他网站

1.2.4 PageRank普遍公式

$$PR(X)=\alpha \sum _{Y_i\in S(X)}\frac{PR(Y_i)}{n_i}+\frac{(1-\alpha )}{N}$$
其中,$S(X)$表示指向网页X的所有网页的集合，$n_i$表示网页$Y_i$的出边数量，即链接网站数；N表示所有网页总数， $\alpha$一般取0.85

二 PageRank的计算方法

2.1 迭代法

利用前面的得到的公式，进行迭代，直到迭代前后两次的差值是在允许的阈值范围内，迭代则结束；在这里，可以将迭代过程写成矩阵形式其推到过程如下

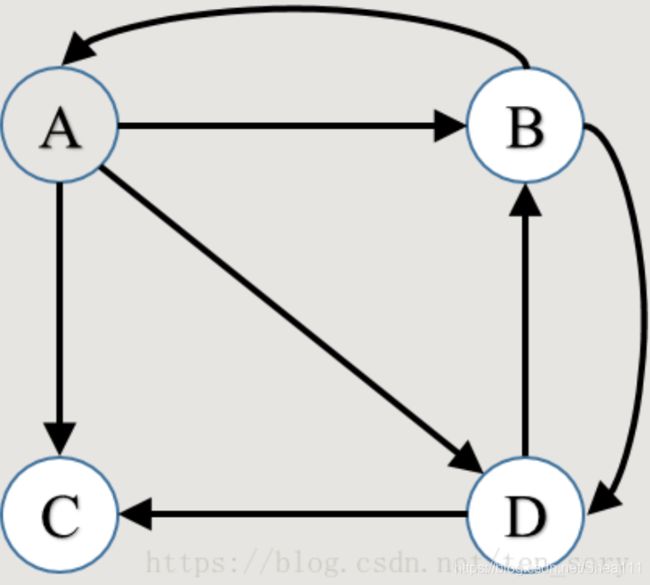
在这里各点的PageRank计算公式应该为：
$$\{\begin{array}{rl}PR(A)& =\alpha (\frac{PR(B)}{2})+\frac{(1-\alpha )}{4}\\ & \\ PR(B)& =\alpha (\frac{PR(A)}{3})+\frac{PR(D)}{2})+\frac{(1-\alpha )}{4}\\ & \\ PR(C)& =\alpha (\frac{PR(A)}{3})+\frac{PR(C)}{1}+\frac{PR(D)}{2})+\frac{(1-\alpha )}{4}\\ & \\ PR(D)& =\alpha (\frac{PR(A)}{3})+\frac{PR(B)}{2})+\frac{(1-\alpha )}{4}\end{array}$$
写成矩阵的形式则为：
$$\left[\begin{array}{c}PR(A)\\ PR(B)\\ PR(C)\\ PR(D)\end{array}\right]=\alpha \left[\begin{array}{cccc}0& \frac{1}{2}& 0& 0\\ & & & \\ \frac{1}{3}& 0& 0& \frac{1}{2}\\ & & & \\ \frac{1}{3}& 0& 1& \frac{1}{3}\\ & & & \\ \frac{1}{3}& \frac{1}{2}& 0& 0\end{array}\right]\left[\begin{array}{c}PR(A)\\ PR(B)\\ PR(C)\\ PR(D)\end{array}\right]+\frac{(1-\alpha )}{4}\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right]$$
将上面的列向量和矩阵分别记为一些符号，可以表示为：
$$\begin{gathered} P_{n+1}=\alpha S{P}_n+\frac{(1-\alpha )}{N}{e}^T \\ 其中，e^T=\left[\begin{array}{c}1\\ 1\\ 1\\ 1\end{array}\right] \end{gathered}$$
更简洁的记法，为：
$$A=aS+\frac{(1-\alpha )}{N}{e}^T$$
其中， A是一个常数矩阵，即迭代公式可以写为：
$$P_{n+1}=A{P}_n$$

2.2 代数法

因为在不断地迭代下去，PageRank算法最终将收敛，而这个时刻的PageRank值组成的列向量应该满足
$$P=\alpha SP+\frac{(1-\alpha )}{N}{e}^T$$
因此有：
$$(E-\alpha S)P=\frac{(1-\alpha )}{N}{e}^T-->P=(E-\alpha S{)}^{-1}\frac{(1-\alpha )}{N}{e}^T$$
这个方法不需要迭代，求出矩阵的逆，就可以求出由PageRank值组成的列向量$P$，但是计算大规模矩阵的逆，虽然代码简单，效率是很低的

三 Python实现

迭代法， 仅需要用numpy库用于矩阵乘法， 这里加入了可视化部分，使用了networkx库来画图

3.1 代码

import numpy as np
import networkx as nx
import  matplotlib.pyplot as plt

if __name__ == '__main__':

    # 读入有向图，存储边
    f = open('input_data.txt', 'r')
    edges = [line.strip('\n').split(' ') for line in f]
    print(edges)


    G = nx.DiGraph()
    for edge in edges:
        G.add_edge(edge[0], edge[1])
    nx.draw(G, with_labels=True)
    plt.show()

    # 根据边获取节点的集合
    nodes = []
    for edge in edges:
        if edge[0] not in nodes:
            nodes.append(edge[0])
        if edge[1] not in nodes:
            nodes.append(edge[1])
    print(nodes)

    N = len(nodes)

    # 将节点符号（字母），映射成阿拉伯数字，便于后面生成A矩阵/S矩阵
    i = 0
    node_to_num = {}
    for node in nodes:
        node_to_num[node] = i
        i += 1
    for edge in edges:
        edge[0] = node_to_num[edge[0]]
        edge[1] = node_to_num[edge[1]]
    print(edges)

    # 生成初步的S矩阵
    S = np.zeros([N, N])
    for edge in edges:
        S[edge[1], edge[0]] = 1
    print(S)

    # 计算比例：即一个网页对其他网页的PageRank值的贡献，即进行列的归一化处理
    for j in range(N):
        sum_of_col = sum(S[:, j])
        # 计算S时，需要考虑没有指出的节点，防止出现NaN，这里需要加个判定
        for i in range(N):
            if sum_of_col != 0:
                S[i, j] /= sum_of_col
            else:
                S[i, j] = 1/N
    print(S)

    # 计算矩阵A
    alpha = 0.85
    A = alpha * S + (1 - alpha) / N * np.ones([N, N])
    print(A)

    # 生成初始的PageRank值，记录在P_n中，P_n和P_n1均用于迭代
    P_n = np.ones(N) / N
    P_n1 = np.zeros(N)

    e = 100000  # 误差初始化
    k = 0  # 记录迭代次数
    print('loop...')

    while e > 0.00000001:  # 开始迭代
        P_n1 = np.dot(A, P_n)  # 迭代公式
        e = P_n1 - P_n
        e = max(map(abs, e))  # 计算误差
        P_n = P_n1
        k += 1
        print('iteration %s:' % str(k), P_n1)

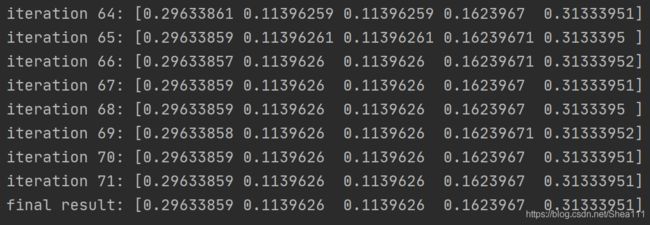
    print('final result:', P_n)

3.2 Result

3.2.1 Graph

3.2.2 Console台

四 PageRank的缺点

参考链接：PageRank算法—从原理到实现

• 没有区分站内导航链接 ，很多网站首页都有对站内其他页面的链接， 称为站内导航链接；这些链接于不同网站之间的链接相比，肯定是后者更能体现PageRank值得传递关系
• 没有过滤广告链接和功能链接（如：分享到xx）
• 对新网页不友好 ，新网页一般入链较少，它要成为一个高的PR值需要很长时间的推广
• 目前对它的改进，有TrustRank 算法

五 缺失值填充

参考链接：python缺失值填充的几种方法

5.1 缺失值的产生机制

1. 完全随机缺失 (Missing Completely at Random)
   某个变量是否确实与它自身的值无关，也和其他任何变量的值无关，如机器故障导致数据缺失
2. 随机缺失 （Missing at Random）
   控制了其他变量已有的值后，某个变量是否确实与他自身的值无关，如人们是否透露收入可能与性别、教育程度、职业等因素有关，如果这些因素都已经观测到，那么虽然收入缺失的比例在不同人群之间有差异，但是在每一类人群内收入是否确实和收入本身的值是无关的，这样收入就是随机缺失的
3. 非随机缺失： （Missing Not at Random）
   即使控制了其他变量已观测到的值， 但是某个变量是否确实依旧和它自身的值有关。例如，在控制了性别、教育程度、职业等已观测因素之后，如果收入是否缺失 依旧依赖于收入本身的值，那么收入就是非随机缺失的

5.2 缺失值的处理

常见的数据缺失填充方式有：删除法、均值法、回归法、KNN、MICE、EM等等
python目前常用的两个包，一个是impyute，第二个fancyimpute。在fancyimpute中继承了很多方法

5.2.1 直接填充

0值/1值填充

data = pd.read_csv(path, encoding = 'gbk')
data = data.fillna(-1)

这种属于单变量补充 ，如果用单一变量的均值/中位数/众数/二分之一最小值/零值进行补植，这种方法会导致数据分布的偏移，方差偏小，PCA上会看到一条补植导致的直线等问题
这种方法只能在缺失数据集满足正态分布 的情况下可以达到比较好的效果，但是在现实应用中，往往连对数据具一定的先验知识都很难做到，但是现实数据往往又不是简单的正态分布，所以使用这个方法不可避免地会造成数据的各种统计参数的扭曲

5.2.2 插值补充

插值法就是通过两点$(x_0,y_0),(x_1,y_1)$估计中间点的值，这里不用把函数先入为主地认为是线性函数

data = pd.read_csv(path, encoding='gbk')
for f in data:	# 插值法补充
	data[f] = data[f].interpolate()
	data.dropna(inplace=True)

其中，interpolate 函数默认采用线性插值 ，即使假设函数是直线形式，缺失值用前一个值和后一个值的平均数填充
也可以根据数字来进行插值，用参数method=‘values’，此时索引的数值实际上就是用来估计y的x值
如果index是时间，我们还可以用method=time来插值，不过当dataframe是多重索引（multiIndex）时，只能用线性插值
此外我们还可以用参数设定采用多项式插值填充等
参考：
戳我①

戳我②

5.2.3 KNN预测缺失值填充

KNN预测的步骤是选择出其他不存在缺失值的列，同时去除掉需要预测确实值得列并且存在缺失值的行，然后计算距离
如果缺失值是离散的，使用K近邻分类器，投票选出K个邻居中最多的类别进行填补，如果为连续变量，则使用K近邻回归器，拿K个邻居中该变量的平均值填补

使用的是fanyimpute库

from fancyimpute import KNN

data = pd.read_csv(path, encoding='gbk'
data = pd.DataFrame(KNN(k=6).fit_transform(data))
data.columns = ['sex', 'age', 'label'] # fancyimpute填补缺失值时会自动删除列名

六 可视化 — 用于绘制直方图、热力图和缺失值可视化

首先读入数据

def read_data():
	path = '...'
	data = pd.read_csv(path, encoding='gbk')
	return data

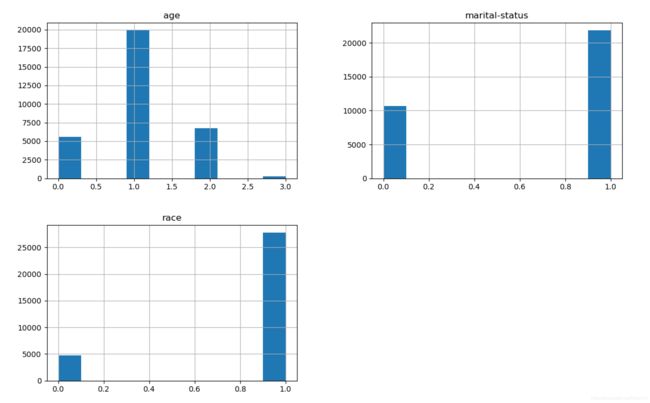
6.1 直方图

import matplotlin.pyplot as plt
def draw(data):
	data.hist(figsize=(16,14))
	plt.savefig("1.jpg", dpi=300, pad_inches = 0)
	plt.show()
data = read_data()
draw(data)

6.2 热力图

热力图表示为数据表里多个特征的两两的相似度
相似度有Pearson相关系数度量：

调用seaborn.heatmap绘制热力图

def draw_hearmap(data):
	ylabels = data.columns.values.tolist()
	
	ss = StandardScaler() # 归一化
	data = ss.fit_transform(data)
	
	df = pd.DataFrame(data)
	
	dfData = df.corr()
	plt.subplots(figsize=(15,15))	#设置画面大小
	sns.heatmap(dfData, annot=True, vmax=1, square=True, yticklabels=ylabels, xticklabels=xlabels,  cmap="RdBu")
	plt.show()

data = read_data()
draw_heatmap(data)

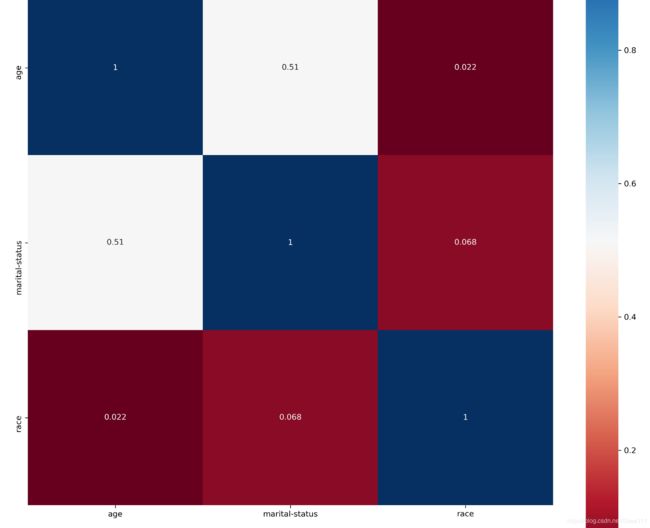
注意： sns.heatmap输入格式需要为DataFrame格式，所以需要将np.array形式的数据转换为DataFrame格式
使用cmap可以改变图的颜色
如果想对坐标轴进行翻转，可以使用.invert_yaxis()函数

6.3 绘制缺失值

使用missingno来绘图

import missingno as msno

msno.matrix(data)	# 矩阵图
msno.bar(data)		# 柱状图
msno.heatmap(data)	# 热力图
msno.dendrogram(data)#树状图

6.4 绘图可以学习的网址

https://blog.csdn.net/weixin_43172660/article/details/83793084
https://blog.csdn.net/Andy_shenzl/article/details/81633356
https://www.helplib.com/GitHub/article_137619