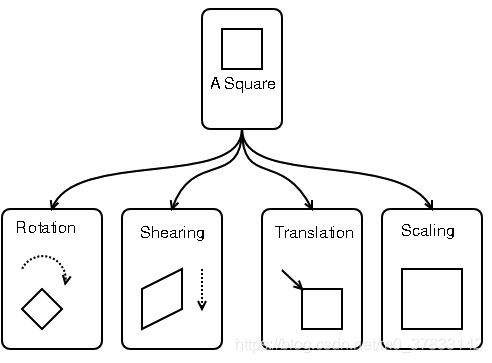
计算机视觉基础-图像仿射变换
Task02 OpenCV框架与图像仿射变换
- 一、仿射变换原理
-
- 1.1仿射变换过程
- 1.2坐标系与变换矩阵
- 二、仿射变换的种类与特点
-
- 2.1仿射变换种类
- 2.2仿射变换特点
- 2.3仿射变换相关函数
-
- 仿射函数
- 翻转函数
- 缩放函数
- 三、基于OpenCV的代码实现
-
- 3.1图像平移
- 3.2图像旋转
- 3.3图像翻转
- 3.4图像剪切(拉伸)
一、仿射变换原理
1.1仿射变换过程
百度词条定义为:
仿射变换,又称仿射映射,是指在几何中,一个向量空间进行一次线性变换并接上一个平移,变换为另一个向量空间。
简单来说就是一个目标图像矩阵是通过源图像矩阵通过一个线性变换+一个平移变换得到的,用坐标矩阵可表述为:
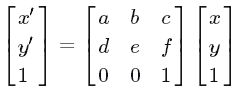
表达式左侧 ( x ′ , y ′ ) (x',y') (x′,y′)表示目标图像,右侧 ( x , y ) (x,y) (x,y)表示源图像,中间的矩阵就是仿射变换中变换矩阵的一般形式,通过对参数 a , b , c , d , e , f a,b,c,d,e,f a,b,c,d,e,f采用不同的约束形式,可得到不同方向、不同形式的仿射变换。参考相关资料,得到一些常见的变换矩阵,形式与作用如下图所示:
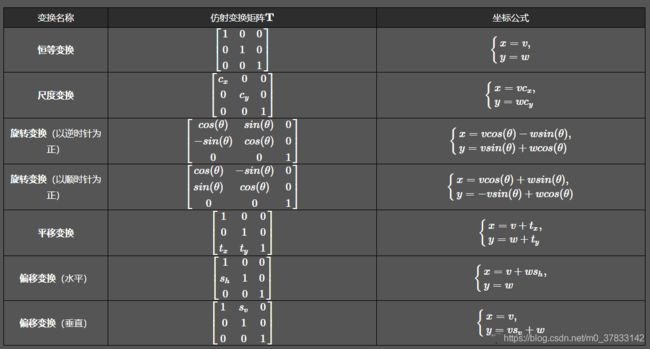
在OpenCV中,这个变换矩阵是通过一个InputArray M实现的,公式表述为:
![]()
dst(x,y)表示目标图像像素点,src(x,y)表示原图像素点;
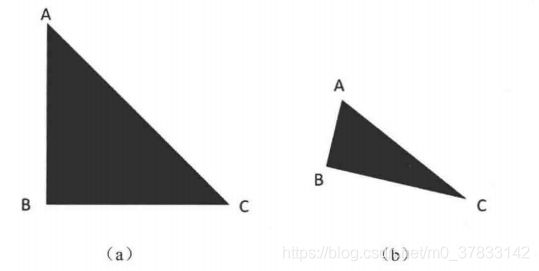
如上图所示,可以通过仿射变换将(a)图变换到(b)图。
1.2坐标系与变换矩阵
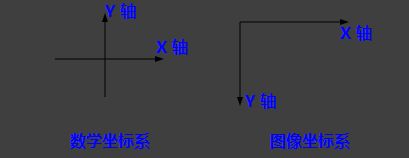
图像矩阵(坐标向量)变换涉及到坐标系的变化,上图所示图像坐标系向右为X轴方向,向下为Y轴方向,在变换过程中,我们只需要知道图像坐标系XY方向即可,避免分不清正反变换。而仿射变换的关键在于变换矩阵,如下图所示:

矩阵坐标系由坐标原点和基向量决定,当坐标系变化,坐标系中的点也跟着变化,但点相对新坐标系( x ′ − y ′ x′−y′ x′−y′坐标系)的位置不变仍为 ( x , y ) (x,y) (x,y),以旋转变换为例,新坐标轴的基向量则变为 [ c o s ( θ ) , s i n ( θ ) ] [cos(θ),sin(θ)] [cos(θ),sin(θ)]和 [ − s i n ( θ ) , c o s ( θ ) ] [−sin(θ),cos(θ)] [−sin(θ),cos(θ)],所以点变化到新位置为:
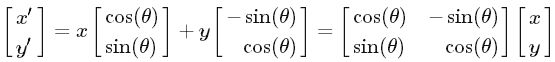
综上:
- 所有变换矩阵只需关注一点:坐标系的变化,即基向量和原点的变化;
- 坐标系变化到哪里,坐标系中的所有点也跟着做同样的变化;
- 坐标系的变换分为基向量的变化以及坐标原点的变化,在变换矩阵,[a d]和[b e]为新的基向量,[c f]为新的坐标原点,先变化基向量,再变化坐标原点;
二、仿射变换的种类与特点
2.1仿射变换种类
- 平移(Translation)
- 缩放(Scale)
- 翻转(Flip)
- 旋转(Rotation)
- 剪切(Shear)
2.2仿射变换特点
平直性:图像经过映射变换后,直线仍然是直线
平行性:图像经过映射变换后,平行线仍然是平行线
2.3仿射变换相关函数
仿射函数
仿射函数warpAffine可实现图像仿射变换,该函数在OpenCV3.0中的语法形式为:
void warpAffine(InputArray src, //原始图像
OutputArray dst, //目标图像,与原始图像类型相同
InputArray M, //一个2×3的变换矩阵
Size dsize, //目标图像的尺度大小
int flags=INTER_LINEAR, //插值方式,默认为双线性插值
int BorderMode=BORDER_CONSTANT, //边类型,默认连续
const Scalar & borderValue=Scalar() //边界值,默认是0
)
【注】当flags=WARP_INVERSE_MAP时,意味着M是逆变换类型,实现从目标图像dst到原始图像src的逆变换,也叫反向映射(Inverse Mapping)。
翻转函数
在OpenCV中图像的翻转通过flip实现,能够实现图像的三种翻转形式:
- 水平方向翻转
- 垂直方向翻转
- 两个方向同时翻转
其函数形式为:
void cv::flip(InputArray src, //原始图像
OutputArray dst, //目标图像
int flipCode //旋转类型
)
【注】flipCode等于0时,表示沿X轴方向翻转;为正数时表示沿Y轴方向翻转;为负数时表示沿XY两个方向同时翻转
缩放函数
在OpenCV中图像的缩放可通过resize实现,具体的函数形式为:
void cv::resize(InoutArray src, //原始图像
OutputArray dst, //目标图像
Size dsize, //目标图像大小
double fx=0, //水平方向变换尺度
double fy=0, //垂直方向变换尺度
int interpolation=INTER_LINEAR //插值方式
)
具体介绍和函数实现,可以参照我的另一篇博客:OpenCV框架与图像插值算法
三、基于OpenCV的代码实现
3.1图像平移
#include 在VS code中编辑代码为:
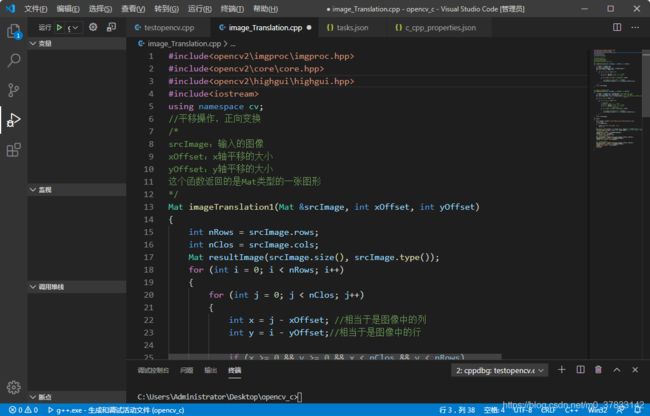
在我的前一篇文章:VS code配置C/C++、OpenCV(Windows)
详细介绍了opencv配置方法。
Output结果为:
原图

正向变换目标图:

逆向变换目标图:
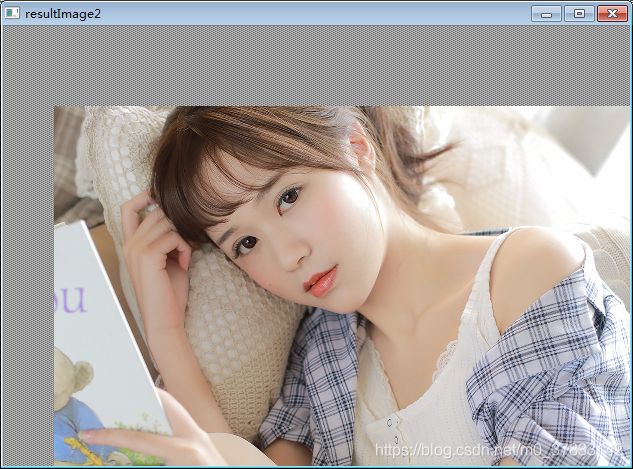
后面在补充一些其他仿射变换Code及效果~
3.2图像旋转
使用getRotationMatrix2D(Point2f center, double angle, double scale) 函数获得图像绕着某一点的旋转矩阵 。
参数解释:
- Point2f center:表示旋转的中心点
- double angle:表示旋转的角度(角度为正值表示向逆时针旋转)
- double scale:图像缩放因子
#include旋转效果图:

【注】当图像宽、高不等时,Center位置若选择(srcImage.rows/2,srcImage.cols/2)会有些许偏差,可以适当调整!
另外,可根据坐标系变换公式:
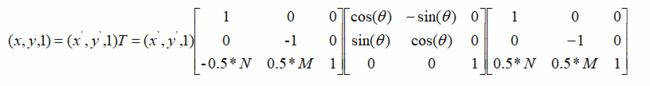
将笛卡尔卡坐标转换为图像坐标,然后将源图像像素点一一映射到目标图像中实现图像旋转。具体代码参考【GitHub:Task2-几何变换
】
其源码如下:
/*图像旋转(以图像中心为旋转中心)*/
void affine_trans_rotate(cv::Mat& src, cv::Mat& dst, double Angle){
double angle = Angle*CV_PI / 180.0;
//构造输出图像
int dst_rows = round(fabs(src.rows * cos(angle)) + fabs(src.cols * sin(angle)));//图像高度
int dst_cols = round(fabs(src.cols * cos(angle)) + fabs(src.rows * sin(angle)));//图像宽度
if (src.channels() == 1) {
dst = cv::Mat::zeros(dst_rows, dst_cols, CV_8UC1); //灰度图初始
}
else {
dst = cv::Mat::zeros(dst_rows, dst_cols, CV_8UC3); //RGB图初始
}
cv::Mat T1 = (cv::Mat_<double>(3,3) << 1.0,0.0,0.0 , 0.0,-1.0,0.0, -0.5*src.cols , 0.5*src.rows , 1.0); // 将原图像坐标映射到数学笛卡尔坐标
cv::Mat T2 = (cv::Mat_<double>(3,3) << cos(angle),-sin(angle),0.0 , sin(angle), cos(angle),0.0, 0.0,0.0,1.0); //数学笛卡尔坐标下顺时针旋转的变换矩阵
double t3[3][3] = { { 1.0, 0.0, 0.0 }, { 0.0, -1.0, 0.0 }, { 0.5*dst.cols, 0.5*dst.rows ,1.0} }; // 将数学笛卡尔坐标映射到旋转后的图像坐标
cv::Mat T3 = cv::Mat(3.0,3.0,CV_64FC1,t3);
cv::Mat T = T1*T2*T3;
cv::Mat T_inv = T.inv(); // 求逆矩阵
for (double i = 0.0; i < dst.rows; i++){
for (double j = 0.0; j < dst.cols; j++){
cv::Mat dst_coordinate = (cv::Mat_<double>(1, 3) << j, i, 1.0);
cv::Mat src_coordinate = dst_coordinate * T_inv;
double v = src_coordinate.at<double>(0, 0); // 原图像的横坐标,列,宽
double w = src_coordinate.at<double>(0, 1); // 原图像的纵坐标,行,高
// std::cout << v << std::endl;
/*双线性插值*/
// 判断是否越界
if (int(Angle) % 90 == 0) {
if (v < 0) v = 0; if (v > src.cols - 1) v = src.cols - 1;
if (w < 0) w = 0; if (w > src.rows - 1) w = src.rows - 1; //必须要加上,否则会出现边界问题
}
if (v >= 0 && w >= 0 && v <= src.cols - 1 && w <= src.rows - 1){
int top = floor(w), bottom = ceil(w), left = floor(v), right = ceil(v); //与映射到原图坐标相邻的四个像素点的坐标
double pw = w - top ; //pw为坐标 行 的小数部分(坐标偏差)
double pv = v - left; //pv为坐标 列 的小数部分(坐标偏差)
if (src.channels() == 1){
//灰度图像
dst.at<uchar>(i, j) = (1 - pw)*(1 - pv)*src.at<uchar>(top, left) + (1 - pw)*pv*src.at<uchar>(top, right) + pw*(1 - pv)*src.at<uchar>(bottom, left) + pw*pv*src.at<uchar>(bottom, right);
}
else{
//彩色图像
dst.at<cv::Vec3b>(i, j)[0] = (1 - pw)*(1 - pv)*src.at<cv::Vec3b>(top, left)[0] + (1 - pw)*pv*src.at<cv::Vec3b>(top, right)[0] + pw*(1 - pv)*src.at<cv::Vec3b>(bottom, left)[0] + pw*pv*src.at<cv::Vec3b>(bottom, right)[0];
dst.at<cv::Vec3b>(i, j)[1] = (1 - pw)*(1 - pv)*src.at<cv::Vec3b>(top, left)[1] + (1 - pw)*pv*src.at<cv::Vec3b>(top, right)[1] + pw*(1 - pv)*src.at<cv::Vec3b>(bottom, left)[1] + pw*pv*src.at<cv::Vec3b>(bottom, right)[1];
dst.at<cv::Vec3b>(i, j)[2] = (1 - pw)*(1 - pv)*src.at<cv::Vec3b>(top, left)[2] + (1 - pw)*pv*src.at<cv::Vec3b>(top, right)[2] + pw*(1 - pv)*src.at<cv::Vec3b>(bottom, left)[2] + pw*pv*src.at<cv::Vec3b>(bottom, right)[2];
}
}
}
}
}
3.3图像翻转
翻转部分主要实现水平、垂直、水平垂直同时翻转三种形式,代码如下:
#include3.4图像剪切(拉伸)
与图像旋转作用相似,图像拉伸同样需要一个中间变量表示拉伸的尺度和方向, 我们需要源图像和目标图像上分别一一映射的三个Point来定义拉伸的形变尺度。具体代码如下:
#include拉升效果图:
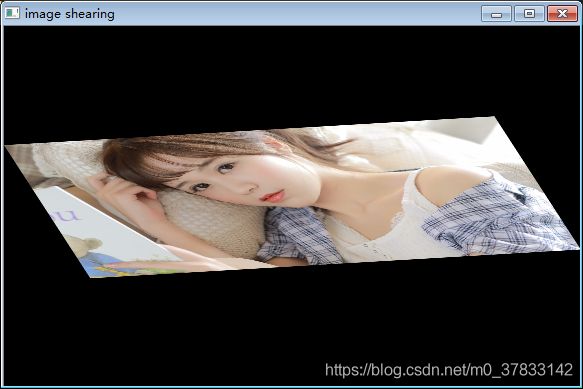
以上就是仿射变换的常用操作,考虑到仿射变换是线性变换,只改变图像相对于坐标系的位置,并不改变像素点之间的相对位置,不考虑实现效率和代码量时候,可以通过两种途径实现代码:
- 直接调用OpenCV相关库函数去实现,如:warpAffine
- 原始图像和目标图像对应像素点一一映射的方式取实现。
好了,今天就更新这么多了!