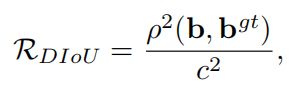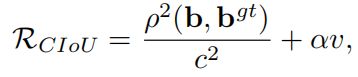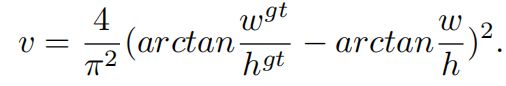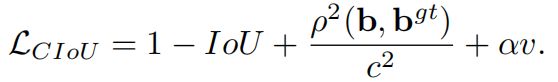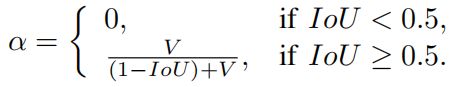IoU Loss汇总
IoU Loss
论文
UnitBox: An Advanced Object Detection Network
解决的问题
用\(l_{2}\) loss作为边框回归loss的两个缺点:
- 在\(l_{2}\) loss中,bounding box的坐标(以\(x_{t},x_{b},x_{l},x_{r}\)的形式)是作为四个单独的变量优化的,这违背了物体的边界是高度相关的事实。这可能会导致预测框和ground truth的某一条或两条边很接近,但整体的框效果很差。
- \(l_{2}\) loss没有归一化,两个像素,一个落在一个大的bounding box中,另一个落在一个小的bounding box中,前者比后者对惩罚的影响更大。这会导致模型更关注大目标,而忽略小目标。
原理
为了解决\(l_{2}\) loss的上述两个缺点,作者提出了IoU loss,具体步骤如下
IoU loss将bbox作为一个整体进行优化,并且其本身就归一化到[0, 1],忽略了bbox的尺度,因此解决了\(l_{2}\) loss的两个缺点。
代码
import torch
def iou_loss(pred, target, eps=1e-6, mode='log'):
"""IoU loss.
Computing the IoU loss between a set of predicted bboxes and target bboxes.
The loss is calculated as negative log of IoU.
Args:
pred (torch.Tensor): Predicted bboxes of shape (B, m, 4) in format or empty.
target (torch.Tensor): Corresponding gt bboxes of shape (B, n, 4) in format or empty.
B indicates the batch dim, in shape (B1, B2, ..., Bn).
eps (float): Eps to avoid log(0).
mode (str): Loss scaling mode, including "linear", "square", and "log".
Default: 'log'
Return:
torch.Tensor: Loss tensor.
"""
bboxes1 = pred.copy()
bboxes2 = target.copy()
batch_shape = bboxes1.shape[:-2]
rows = bboxes1.size(-2)
cols = bboxes2.size(-2)
if rows * cols == 0:
return bboxes1.new(batch_shape + (rows, cols))
area1 = (bboxes1[..., 2] - bboxes1[..., 0]) * (
bboxes1[..., 3] - bboxes1[..., 1])
area2 = (bboxes2[..., 2] - bboxes2[..., 0]) * (
bboxes2[..., 3] - bboxes2[..., 1])
lt = torch.max(bboxes1[..., :, None, :2],
bboxes2[..., None, :, :2]) # [B, rows, cols, 2]
rb = torch.min(bboxes1[..., :, None, 2:],
bboxes2[..., None, :, 2:]) # [B, rows, cols, 2]
wh = (rb - lt).clamp(min=0)
overlap = wh[..., 0] * wh[..., 1]
union = area1[..., None] + area2[..., None, :] - overlap
eps = union.new_tensor([eps])
union = torch.max(union, eps)
ious = overlap / union
ious = ious.clamp(min=eps) # avoid log(0)
if mode == 'linear':
loss = 1 - ious
elif mode == 'square':
loss = 1 - ious**2
elif mode == 'log':
loss = -ious.log()
else:
raise NotImplementedError
return loss
GIoU Loss
论文
Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression
解决的问题
当pred box和gt box不重叠,即IoU=0时,此时IoU无法反映它们是挨得很近还是离得很远,\(L_{IoU}=1-IoU\)始终为1,无法给出优化方向。
原理
因此作者提出了GIoU,GIoU的公式如下,在目标检测中\(A、B\)都是矩形,这里\(C\)是包含\(A、B\)的最小矩形,\(C\setminus(A\cup B)\)是\(C\)没有覆盖\(A、B\)区域的面积。
具体计算步骤如下
IoU的取值范围是[0, 1],GIoU的取值范围是[-1, 1]。当A、B完全重合时,GIoU=IoU=1。当\(\lim_{\frac{|A\cup B|}{|c|}\rightarrow 0}\)时,GIoU=-1。当IoU=0时,\(L_{GIoU}=1-GIoU=2-\frac{|A\cup B|}{|C|}\),可以看出当\(A、B\)的面积不变时,它们离得越远C就越大,从而loss也越大,loss的优化方向就是使pred box离gt box越来越近。
代码
import torch
def giou_loss(pred, target, eps=1e-6, mode='log'):
"""IoU loss.
Computing the IoU loss between a set of predicted bboxes and target bboxes.
The loss is calculated as negative log of IoU.
Args:
pred (torch.Tensor): Predicted bboxes of shape (B, m, 4) in format or empty.
target (torch.Tensor): Corresponding gt bboxes of shape (B, n, 4) in format or empty.
B indicates the batch dim, in shape (B1, B2, ..., Bn).
eps (float): Eps to avoid log(0).
mode (str): Loss scaling mode, including "linear", "square", and "log".
Default: 'log'
Return:
torch.Tensor: Loss tensor.
"""
bboxes1 = pred.copy()
bboxes2 = target.copy()
batch_shape = bboxes1.shape[:-2]
rows = bboxes1.size(-2)
cols = bboxes2.size(-2)
if rows * cols == 0:
return bboxes1.new(batch_shape + (rows, cols))
area1 = (bboxes1[..., 2] - bboxes1[..., 0]) * (
bboxes1[..., 3] - bboxes1[..., 1])
area2 = (bboxes2[..., 2] - bboxes2[..., 0]) * (
bboxes2[..., 3] - bboxes2[..., 1])
lt = torch.max(bboxes1[..., :, None, :2],
bboxes2[..., None, :, :2]) # [B, rows, cols, 2]
rb = torch.min(bboxes1[..., :, None, 2:],
bboxes2[..., None, :, 2:]) # [B, rows, cols, 2]
wh = (rb - lt).clamp(min=0)
overlap = wh[..., 0] * wh[..., 1]
union = area1[..., None] + area2[..., None, :] - overlap
eps = union.new_tensor([eps])
union = torch.max(union, eps)
ious = overlap / union
# 比iou多的部分
enclosed_lt = torch.min(bboxes1[..., :, None, :2],
bboxes2[..., None, :, :2])
enclosed_rb = torch.max(bboxes1[..., :, None, 2:],
bboxes2[..., None, :, 2:])
enclose_wh = (enclosed_rb - enclosed_lt).clamp(min=0)
enclose_area = enclose_wh[..., 0] * enclose_wh[..., 1]
enclose_area = torch.max(enclose_area, eps)
gious = ious - (enclose_area - union) / enclose_area
gious = gious.clamp(min=eps) # avoid log(0)
if mode == 'linear':
loss = 1 - gious
elif mode == 'square':
loss = 1 - gious**2
elif mode == 'log':
loss = -gious.log()
else:
raise NotImplementedError
return loss
DIoU Loss
论文
Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression
解决的问题
GIoU的两个缺点
- 收敛慢
- 回归不准确
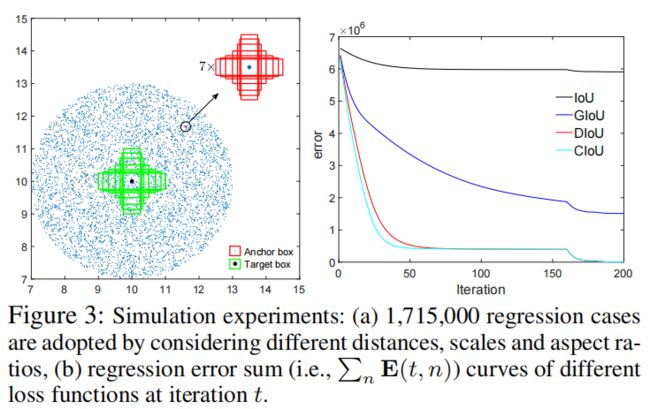
作者通过模拟实验得到使用不同loss时,box的回归误差。实验的设计为:7个中心在坐标(10,10)处,面积为1,宽高比分比为1:4,1:3,1:2,1:1,2:1,3:1,4:1的box作为target box,如下图中绿色box所示。anchor box均匀的放置在以坐标(10,10)为中心半径为3的区域内的5000个点上,即下图中的蓝色点。每个点放置7种尺度7种宽高比共49个anchor,尺度分别为0.5,0.67,0.75,1.33,1.5,2,宽高比和target box的一致。因此一共有5000×7×7×7=1715000个回归实例。
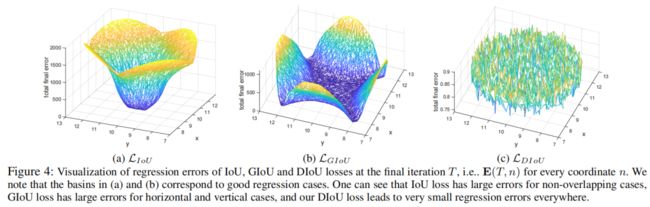
在200个epoch后,每个点处的回归误差如下图所示。其中(a)是IoU loss的回归误差,可以看出只有当anchor和gt box有重叠时误差才比较小。(b)是GIoU loss的回归误差,可以看出相比于IoU loss,basin区域更多也就是GIoU起作用的区域,但是在水平和垂直方向误差仍较大。
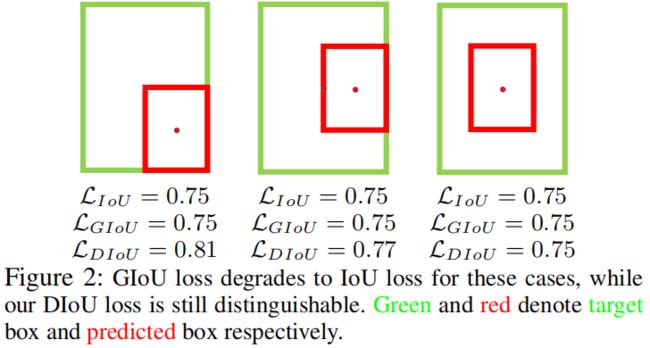
\(L_{GIoU}=1-IoU+\frac{|C-B\cup B^{gt}|}{|B|}\),从GIoU loss的公式可以看出,其中的penalty term是用来减小\(|C-A\cup B|\)的,但是当它们相交或是包含时\(C-A\cup B\)的面积很小甚至为0,此时GIoU loss几乎退化成IoU loss,如下图所示。在学习率合适的时候只要迭代次数足够多,GIoU是会收敛的比较好,但是收敛速度很慢。
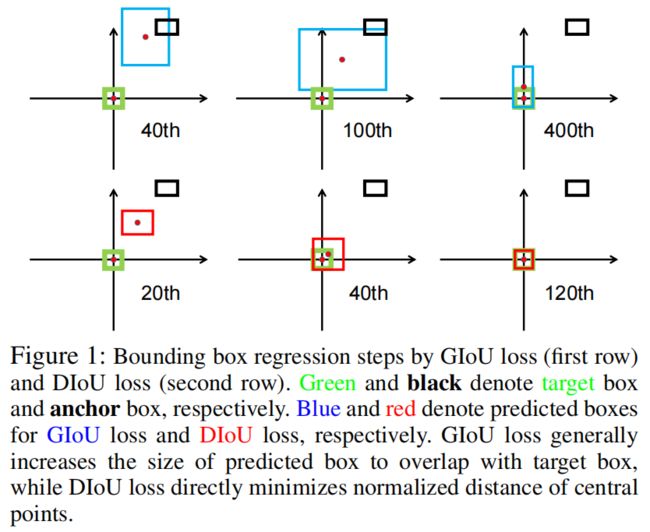
从下面这张图可以看出,GIoU是首先增加预测框的大小使其与目标重合,然后IoU项再使预测框与目标匹配,从而导致收敛慢。
原理
IoU-based loss都可以表示成\(L=1-IoU+R(B,B^{gt})\)的形式,其中\(R(B,B^{gt})\)是惩罚项。作者将惩罚项定义成anchor和gt中心点之间的距离,具体如下
其中\(\mathbf{b}\)和\(\mathbf{b}^{gt}\)分别表示\(B\)和\(B^{gt}\)的中心点,\(\rho (\cdot )\)是欧式距离,\(c\)是anchor和gt box的最小外接矩形的对角线长度。Distance-IoU Loss可以定义成如下形式
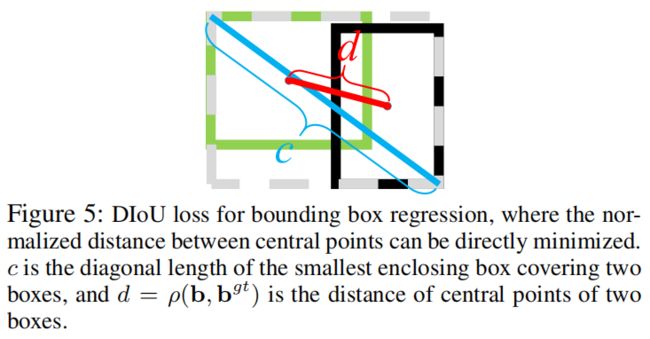
如下图所示,DIoU loss直接最小化两个中心点之间的距离,而GIoU loss旨在最小化\(C-B\cup B^{gt}\)的面积。
DIoU loss继承了IoU loss和GIoU loss的一些属性
- DIoU loss对回归尺度不敏感。
- 和GIoU loss一样,当预测框和目标框不重合时,仍能提供梯度优化方向。
-
当两个框完全重合时,\(L_{IoU}=L_{GIoU}=L_{DIoU}=0\),当两个框离很远时,\(L_{GIoU}=L_{DIoU}\rightarrow 0\)。
同时相比于IoU loss和GIoU loss,DIoU loss还有一些优点
- DIoU loss直接最小化两个框的距离,因此比GIoU loss收敛更快。
- 当两个框是包含关系时,或沿水平和垂直方向时,GIoU loss几乎退化成IoU loss,而DIoU loss仍能继续快速收敛。
代码
def diou_loss(pred, target, eps=1e-7):
r"""`Implementation of Distance-IoU Loss: Faster and Better
Learning for Bounding Box Regression, https://arxiv.org/abs/1911.08287`_.
Code is modified from https://github.com/Zzh-tju/DIoU.
Args:
pred (Tensor): Predicted bboxes of format (x1, y1, x2, y2),
shape (n, 4).
target (Tensor): Corresponding gt bboxes, shape (n, 4).
eps (float): Eps to avoid log(0).
Return:
Tensor: Loss tensor.
"""
# overlap
lt = torch.max(pred[:, :2], target[:, :2])
rb = torch.min(pred[:, 2:], target[:, 2:])
wh = (rb - lt).clamp(min=0)
overlap = wh[:, 0] * wh[:, 1]
# union
ap = (pred[:, 2] - pred[:, 0]) * (pred[:, 3] - pred[:, 1])
ag = (target[:, 2] - target[:, 0]) * (target[:, 3] - target[:, 1])
union = ap + ag - overlap + eps
# IoU
ious = overlap / union
# enclose area
enclose_x1y1 = torch.min(pred[:, :2], target[:, :2])
enclose_x2y2 = torch.max(pred[:, 2:], target[:, 2:])
enclose_wh = (enclose_x2y2 - enclose_x1y1).clamp(min=0)
cw = enclose_wh[:, 0]
ch = enclose_wh[:, 1]
c2 = cw**2 + ch**2 + eps
b1_x1, b1_y1 = pred[:, 0], pred[:, 1]
b1_x2, b1_y2 = pred[:, 2], pred[:, 3]
b2_x1, b2_y1 = target[:, 0], target[:, 1]
b2_x2, b2_y2 = target[:, 2], target[:, 3]
left = ((b2_x1 + b2_x2) - (b1_x1 + b1_x2))**2 / 4
right = ((b2_y1 + b2_y2) - (b1_y1 + b1_y2))**2 / 4
rho2 = left + right
# DIoU
dious = ious - rho2 / c2
loss = 1 - dious
return lossCIoU Loss
论文
Enhancing Geometric Factors in Model Learning and Inference for Object Detection and Instance Segmentation
解决的问题
作者提出对于边框回归问题,一个好的Loss应该考虑到三个重要的几何因素,即重叠面积、中心点距离、宽高比。IoU loss考虑到了重叠面积,GIoU loss严重依赖于IoU loss,DIoU loss进一步考虑到了中心点距离,但还有一个因素宽高比没有考虑到。
原理
因此在DIoU loss的基础上,融入宽高比一致性的考虑,提出了Complete IoU Loss。CIoU loss的惩罚项如下所示
其中\(\alpha\)是一个正的权重参数,\(v\)衡量了宽高比的一致性
CIoU loss的完整表达如下
权重参数\(\alpha\)的定义如下
代码
def ciou_loss(pred, target, eps=1e-7):
r"""`Implementation of paper `Enhancing Geometric Factors into
Model Learning and Inference for Object Detection and Instance
Segmentation `_.
Code is modified from https://github.com/Zzh-tju/CIoU.
Args:
pred (Tensor): Predicted bboxes of format (x1, y1, x2, y2),
shape (n, 4).
target (Tensor): Corresponding gt bboxes, shape (n, 4).
eps (float): Eps to avoid log(0).
Return:
Tensor: Loss tensor.
"""
# overlap
lt = torch.max(pred[:, :2], target[:, :2])
rb = torch.min(pred[:, 2:], target[:, 2:])
wh = (rb - lt).clamp(min=0)
overlap = wh[:, 0] * wh[:, 1]
# union
ap = (pred[:, 2] - pred[:, 0]) * (pred[:, 3] - pred[:, 1])
ag = (target[:, 2] - target[:, 0]) * (target[:, 3] - target[:, 1])
union = ap + ag - overlap + eps
# IoU
ious = overlap / union
# enclose area
enclose_x1y1 = torch.min(pred[:, :2], target[:, :2])
enclose_x2y2 = torch.max(pred[:, 2:], target[:, 2:])
enclose_wh = (enclose_x2y2 - enclose_x1y1).clamp(min=0)
cw = enclose_wh[:, 0]
ch = enclose_wh[:, 1]
c2 = cw**2 + ch**2 + eps
b1_x1, b1_y1 = pred[:, 0], pred[:, 1]
b1_x2, b1_y2 = pred[:, 2], pred[:, 3]
b2_x1, b2_y1 = target[:, 0], target[:, 1]
b2_x2, b2_y2 = target[:, 2], target[:, 3]
w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
left = ((b2_x1 + b2_x2) - (b1_x1 + b1_x2))**2 / 4
right = ((b2_y1 + b2_y2) - (b1_y1 + b1_y2))**2 / 4
rho2 = left + right
factor = 4 / math.pi**2
v = factor * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
with torch.no_grad():
alpha = (ious > 0.5).float() * v / (1 - ious + v)
# CIoU
cious = ious - (rho2 / c2 + alpha * v)
loss = 1 - cious.clamp(min=-1.0, max=1.0)
return loss