multigrid多重网格数值算法Octave/Matlab程序

Afivo框架用到了multigrid方法求解PDE方程，需要先简单理解一下multigrid的原理，找到了视频教程和对应的octave代码，先在博客中记录备忘。
参考来源：

• https://www.youtube.com/watch?v=mBTIX9CJGTc&t=202s
• 雅克比迭代：https://en.wikipedia.org/wiki/Jacobi_method
  - 高斯赛德尔迭代：https://en.wikipedia.org/wiki/Gauss%E2%80%93Seidel_method
  

代码 (matlab环境运行需要简单修改一下代码，笔者补充了高斯赛德尔的迭代方式）：

clc; % Clear console
clear all; % Clear variables from previous runs
close all; % Close open figure windows
format bank % Numbers with two decimal points, for better overview in console
%
% === PARAMETERS ===
%
% Initial (finest) matrix dimension
% Best choices for maintaining integral number of nodes
% over multiple coarsening steps: (2^n)+1 )
dim = 177;  % 矩阵维度
% Number of grid levels used (=Number of coarsening steps - 1)
% If this is 1, the program effectively degenerates
% to just one standard Jacobi method application on the initial system
% If above, dim = (2^n)+1, this number must not be lower than n+1.
N_grids=3;
% Number of smoother (Jacobi) iterations per coarsening step
N_smoother = 3;
% Choices of initial systems to highlight different aspects of the solver.
% 1 = Pure 1D Poisson system. (compare https://people.sc.fsu.edu/~jburkardt/...
% classes/math2071_2020/poisson_steady_1d/poisson_steady_1d.pdf
% Is useful to see how pure Jacobi method fails hopelessly,
% while Multigrid still does pretty ok.
% 2 = Sparsity pattern equal to 1, but with some induced randomness.
% Best choice to actually see the strengths of Multigrid.
% 3 = Diagonally dominated matrix (as Jacobi requires), but full-density
% instead of sparse. Pure Jacobi converges almost immediately here,
% while Multigrid fails totally. (Don't ask me why, I have no idea.)
initial_system = 2;
% Recommended starting parameters if you have no idea what you want:
% 17, 3, 1, 2 from top to bottom.
%
%
% === INITIAL SYSTEMS ===
%
% Unit vector used as a base for creating the systems.
unit_vector = ones(dim,1);
% Zero vector as initial guess for all systems. (From what I've read,
% trying to get initial guesses that are closer to the solution
% doesn't only not help much, but can actually do harm if you get it wrong.
% So I decided to just stick with the zero vector for this program.)
x_0 = zeros(dim,1);
% System 1, as described above
if initial_system == 1
  A_diag = diag(2*unit_vector);
  A_upper = diag(-unit_vector(1:end-1),1);
  A_lower = diag(-unit_vector(1:end-1),-1);
  A = A_diag + A_upper + A_lower;
  % b = 50*unit_vector;
  b = 100*rand(dim,1).*unit_vector;
% System 2, as described above
elseif initial_system == 2
  for k=1:dim
    diagonal_vector_middle(k,1) = 2 + rand()*mod(k,2);
  endfor
  for k=1:dim-1
    diagonal_vector_upper(k,1) = -1 + 0.5*rand()*mod(k,2);
    diagonal_vector_lower(k,1) = -1 + 0.5*rand()*mod(k,2);
  endfor
  A_diag = diag(diagonal_vector_middle);
  A_upper = diag(diagonal_vector_upper,1);
  A_lower = diag(diagonal_vector_lower,-1);
  A = A_diag + A_upper + A_lower;
  b = ceil(100*rand(dim,1));
% System 3, as described above
elseif initial_system == 3
  A_rand = rand(dim,dim);
  A_diag = diag(dim/2*unit_vector + rand(dim,1));
  A = A_diag + A_rand;
  b = 100*rand(dim,1);
else
  error('Error: Initial system not defined.')
end
M = A;
disp(A)
disp(b)

% === FUNCTIONS ===
%
% Jacobi method 雅克比迭代
% Perform N jacobi iterations on system A*x = b with initial guess x_in
% see https://en.wikipedia.org/wiki/Jacobi_method
function x_out = jacobi_method(x_in, A, b, N)
  D = diag(diag(A));
  L = tril(A,-1);
  U = triu(A,1);
  LU = L+U;
  D_inv = diag(diag(A).^-1);
  % 迭代格式 x(k+1)=M*x(k) + g
  M = D_inv*LU;
  g = D_inv*b;
  % Checking if spectral radius < 1 (see wiki article section 'Convergence')
  if max(abs(eig(D_inv*LU))) >= 1
    error('Spectral radius of iteration matrix is 1 or higher')
  endif
  for i = 1:N
    x_out = D_inv*(b-(LU)*x_in);
    % x_out = M*x_in + g;
    x_in = x_out;
  endfor
endfunction

% Gauss-Seidel method 高斯赛德尔迭代
% Perform N jacobi iterations on system A*x = b with initial guess x_in
% x(k+1) = L*^{-1}*(b - U*x(k)), L*=L+D
% see https://en.wikipedia.org/wiki/Gauss%E2%80%93Seidel_method
function x_out = gauss_seidel_method(x_in, A, b, N)
  D = diag(diag(A));
  L = tril(A,-1);
  U = triu(A,1);
  LU = L+U;
  L_star = L+D;
  D_inv = diag(diag(A).^-1);

  % Checking if spectral radius < 1 (see wiki article section 'Convergence')
  % 检查谱半径是否小于1
  if max(abs(eig(D_inv*LU))) >= 1
    error('Spectral radius of iteration matrix is 1 or higher')
  endif
  for i = 1:N
    x_out = inv(L_star)*(b - U*x_in);
    x_in = x_out;
  endfor
endfunction

%
% Restriction matrix
% Rectangular matrix that scales down a vector of size dim to ceil(dim/2).
% New node (n)_new = 1/4*(n-1)_old + 1/2*(n)_old + 1/4*(n+1)_old
% I couldn't find any reference for how exactly these matrices are supposed
% to look like, so I made this guess. Seems to work alright.
function R = restrict_matrix(dim);
  dim_1 = ceil(dim/2);
  dim_2 = dim;
  R = zeros(dim_1, dim_2);
  R(1,1)=3/4;
  R(1,2)=1/4;
  R(dim_1,dim_2)=3/4;
  R(dim_1,dim_2-1)=1/4;
  for k=2:dim_1-1
    R(k,2*k-2)=1/4;
    R(k,2*k-1)=1/2;
    R(k,2*k)=1/4;
  endfor
endfunction
%
% Prolong matrix
% Scales a vector of size dim up to 2*dim+1
% Already existing node values are kept, in-between nodes are interpolated
% from their two neighbors by (n)_new = 1/2*(n-1)_old + 1/2*(n+1)_old
% Same as above: Just a guess, but seems to work.
function P = prolong_matrix(dim);
  dim_1 = dim;
  dim_2 = ceil(dim/2);
  P = zeros(dim_1, dim_2);
  P(1,1)=1;
  P(2,1)=1/2;
  P(dim_1-1, dim_2)=1/2;
  P(dim_1, dim_2)=1;
  for k=2:dim_2-1
    P(2*k-2,k)=1/2;
    P(2*k-1,k)=1;
    P(2*k,k)=1/2;
  endfor
endfunction
%
% Coarsening step
% Smoothes the inital system by applying N_smoother Jacobi steps,
% Then coarsens the grid and creates the new system
% A_coarse * error = r_coarse.
function [x_smooth, A_coarse, r_coarse] = AMG_coarsen(A, b, x_0, N_smoother)
  dim = length(x_0);
  x_smooth = jacobi_method(x_0, A, b, N_smoother);
  P = prolong_matrix(dim);
  R = restrict_matrix(dim);
  r = b - A*x_smooth;
  r_coarse = R*r;
  A_coarse = R*A*P;
endfunction
%
% Refinement step
% Takes the (coarse) result error of a coarsening step,
% refines it and adds it to the next-finer error.
function x = AMG_refine(x_fine, x_coarse)
  dim = length(x_fine);
  P = prolong_matrix(dim);
  x = x_fine + P*x_coarse;
endfunction
%
%
% === REFERENCE SOLUTIONS ===
%
% Exact solution for evaluating the accuracy of our solvers
% A\b is a more efficient version of inv(A)*b, the solution of A*x = b.
x_exact = A\b;
% Solution we would get if we applied the same overall number of Jacobi
% iterations, but without the Multigrid coarsening/refinements in between.
x_single_jacobi = jacobi_method(x_0, A, b, N_smoother*N_grids);
x_single_gauss_seidel = gauss_seidel_method(x_0, A, b, N_smoother*N_grids);

% Plot both solutions in figure
% Adjust position as needed. Parameters are in pixels from left to right:
% Horizontal distance from bottom left of screen to bottom left of figure,
% vertical distance from bottom left of screen to bottom left of figure,
% width of figure, height of figure.
fig = figure('Position',[920 40 1500 1100]); %lower left corner and width and height
xlim([0 dim-1]);
hold on
% Exact solution is very thick and bright green
plot((1:dim)-1,x_exact,'g','LineWidth',5,'DisplayName','Exact Solution')
% Pure Jacobi solution is thick and red
plot((1:dim)-1,x_single_jacobi,'color',[1,0.3,0.3],...
'LineWidth',2,'DisplayName','Pure Jacobi method without MG')
% Pure Gauss-seidel solution is thick and black
plot((1:dim)-1,x_single_gauss_seidel,'color',[0,0.0,0.0],...
'LineWidth',2,'DisplayName','Pure Gauss-Seidel method without MG')
%
%
% === MULTIGRID ALGORITHM ===
%
% Calculate dimensions of coarsened systems. This is needed in multiple spots,
% so it makes sense to just do it once here.
for k = 1:N_grids
  if k == 1
    dim_at_refinement_level = dim;
  else
    dim_at_refinement_level(k) = ceil(dim_at_refinement_level(k-1)/2);
  endif
  if mod(dim_at_refinement_level(k),2)==0 && k != N_grids
    error('Error: Cant coarsen further. Dimension must be natural number.')
  endif
endfor
disp("dim_at_refinement_level:"), disp(dim_at_refinement_level)
%
% Coarsening loop
% From the second iteration on, we are replacing b by the residual
% r = A*x - b, which means we are solving for the error
% e=x-x_exact instead of x.
disp("MG Coarsening loop")
for k = 1:N_grids
  dim_fine = dim_at_refinement_level(k);
  disp("dim_fine:"),disp(dim_fine)
  step_width_plot = 2^(k-1);
  [x_smooth, A_coarse, r_coarse] = AMG_coarsen(A, b, x_0, N_smoother);
  x_store(1:dim_fine,k) = x_smooth;
  % Result of smoother (thin and turquoise with circular markers).
  % 'HandleVisibility','off' keeps it from appearing in the legend.
  % I didn't want one entry per coarsening step cluttering the legend,
  % so instead I left it out all together.
  plot(step_width_plot*((1:dim_fine)-1),x_smooth,...
  'color',[0.4,0.8,0.8],'marker','o','HandleVisibility','off');
  if k != N_grids
    A=A_coarse;
    b=r_coarse;
    x_0 = zeros(length(A_coarse),1);
  endif
endfor
%
% Refinement loop
% Adding all the errors from the coarsening steps to the approximate x
% from the first coarsening step yields the overall Multigrid solution.
disp("MG Refinement loop")
if N_grids > 1
  x_coarse = x_store(1:dim_at_refinement_level(end),end);
  for k = 1:N_grids-1
    dim_fine = dim_at_refinement_level(end-k);
    step_width_plot = 2^(N_grids-k-1);
    x_fine = x_store(1:dim_at_refinement_level(end-k),end-k);
    x_refined = AMG_refine(x_fine, x_coarse);
    if k < N_grids-1
      % Intermediate solution (thin and blue-green(ish) with square markers.
      plot(step_width_plot*((1:dim_fine)-1),x_refined,...
      'color',[0.2,0.5,0.5],'marker','s','HandleVisibility','off');
    else
      % Overall Multigrid solution (thick and blue).
      plot(step_width_plot*((1:dim_fine)-1),x_refined,...
      'color',[0.5,0.5,1],'marker','*','LineWidth',2,'DisplayName','MG solution');
    endif
    x_coarse = x_refined;
  endfor
endif
%
set(gca,'FontName','Times New Roman','FontSize',28)%设置坐标轴刻度字体名称，大小
grid minor on;
legend('FontName','Times New Roman') % Print legend in plot.

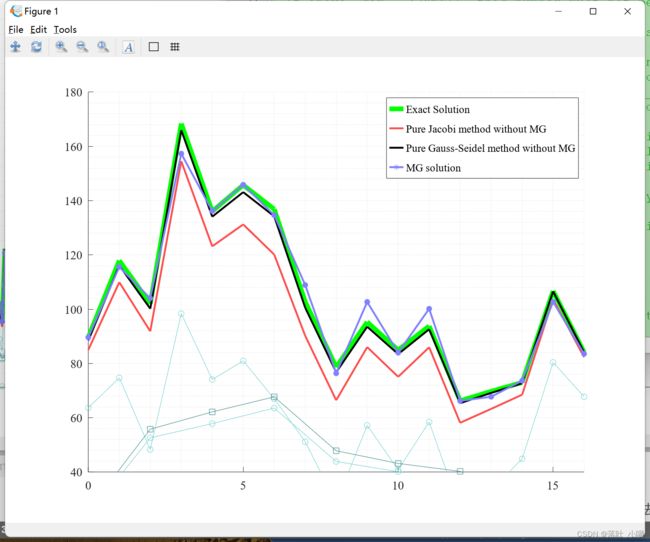
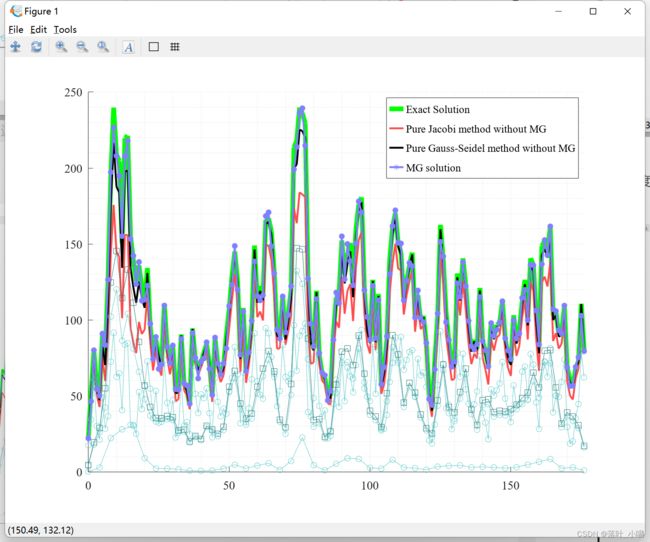
结果如下：

• 矩阵维度：17
  

• 矩阵维度：177
  

可见multigrid（MG）方法在求解大型线性方程组具有一定的优越性。