隐马尔可夫模型
隐马尔可夫模型详解(HMM)
隐马尔可夫模型的详细版本,添加了实例和具体公式,便于理解。
欢迎纠错

马尔可夫模型
概念导入
在某段时间内,交通信号灯的颜色变化序列是:红色 - 黄色 - 绿色 - 红色。
在某个星期天气的变化状态序列:晴朗 - 多云 - 雨天。
像交通信号灯一样**,某一个状态只由前一个状态决定**,这就是一个一阶马尔可夫模型。而像天气这样,天气状态间的转移仅依赖于前 n 天天气的状态,即状态间的转移仅依赖于前 n 个状态的过程。这个过程就称为n 阶马尔科夫模型。
(关键是依赖于前几个状态)
不通俗的讲,马尔可夫模型(Markovmodel)描述了一类重要的随机过程,随机过程又称随机函数,是随时间而随机变化的过程。(随时间而随机变化的过程)
马尔可夫模型定义
存在一类重要的随机过程,如果一个系列有N个状态: S 1 , S 2 , . . . , S N S_1,S_2,...,S_N S1,S2,...,SN随时间的推移,该系统从某一状态转移到另一个状态,如果用 q t q_t qt表示系统在时间 t t t的状态变量,那么 t t t时刻状态的取值为 S j S_j Sj,(1<=j<=N)的概率取决于前 t − 1 t - 1 t−1个时刻,( 1 , 2. ⋯ t − 1 1,2.\cdots t-1 1,2.⋯t−1的状态,该概率为:
(状态变量、状态取值)
$ P ( q t = S j ∣ q t − 1 = S i , q t − 2 = S k , ⋯ ) P(q_t = S_j | q_{t - 1} = S_i,q_{t - 2}= S_k,\cdots) P(qt=Sj∣qt−1=Si,qt−2=Sk,⋯)
假设一:如果在特定情况下,系统在时间 t t t的状态只与其在 t − 1 t - 1 t−1时刻状态相关,则该系统构成一个离散的一阶马尔可夫链。
P ( q t = S j ∣ q t − 1 = S i , q t − 2 = S k , ⋯ ) = P ( q t = S j ∣ q t − 1 = S i ) P(q_t = S_j | q_{t - 1} = S_i,q_{t - 2}= S_k,\cdots) = P(q_t = S_j| q_{t - 1} = S_i) P(qt=Sj∣qt−1=Si,qt−2=Sk,⋯)=P(qt=Sj∣qt−1=Si)
假设二:如果只考虑独立于时间 t t t的随机过程,状态与时间无关,那么 P ( q t = S j ∣ q t − 1 = S i ) = a i j , 1 < = i , j < = N P(q_t = S_j| q_{t - 1} = S_i) = a_{ij},1<=i,j<=N P(qt=Sj∣qt−1=Si)=aij,1<=i,j<=N
t t t时刻状态概率取决于前 t − 1 t - 1 t−1时刻 1 , 2 , ⋯ t − 1 1,2,\cdots t - 1 1,2,⋯t−1的状态,且状态的转换与时间无关,则该随机过程是马尔可夫模型。
隐马尔可夫模型
概念导入
在马尔可夫模型中,每个状态代表了一个可观察的事件,所以,马尔可夫模型有时又称作可视马尔可夫模型(visibleMarkovmodel,VMM),这在某种程度上限制了模型的适应性。
对于盲人来说也许不能够直接获取到天气的观察情况,但是他可以通过触摸树叶通过树叶的干燥程度判断天气的状态。于是天气就是一个隐藏的状态,树叶的干燥程度是一个可观察的状态,于是我们就有了两组状态,一个是不可观察、隐藏的状态(天气),一个是可观察的状态(树叶),我们希望设计一种算法,在不能够直接观察天气的情况下,通过树叶和马尔可夫假设来预测天气。
一个一阶乘马尔可夫链路描述:
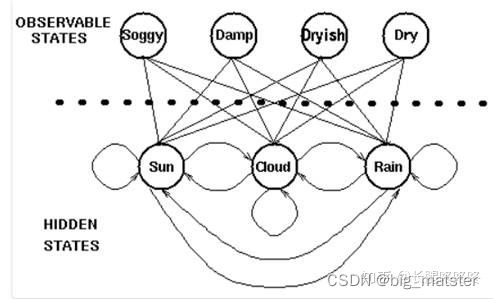
在隐马尔可夫模型(HMM)中,我们不知道模型具体的状态序列,只知道状态转移的概率,即模型的状态转换过程是不可观察的。
因此,该模型是一个双重随机过程,包括模型的状态转换和特定状态下可观察事件的随机
HMM组成
例如:N个袋子,每个袋子有M种不同颜色的球,选择一个袋子,取出一个球,得到球的颜色。
- 状态数为N(袋子数量)
- 每个状态可能的符号数M(不同颜色球的数目)
- 状态转移概率矩阵 A = a i j A = a_{ij} A=aij
(从一只袋子状态 S i S_i Si转向另一只袋子状态 S j S_j Sj的取球概率. - 从状态 S j Sj Sj观察到某一特定符号 vk 的概率分布矩阵为: (从第 j 个袋子中取出第 k 种颜色的球的概率)
- 初始状态的概率分布为 π = π i \pi = \pi_i π=πi
一般将一个马尔可夫模型记为: λ = [ π , A , B ] \lambda = [\pi,A,B] λ=[π,A,B]
需要确定以下三方面内容:
- 设置 t = 1 t = 1 t=1,并根据初始状态概率 π \pi π选择初始状态 Y 1 Y_1 Y1;
- 根据状态值和输出观测概率B选择观测变量取值 X t X_t Xt
- 根据状态值和状态转移矩阵A转移模型状态,即确定 Y t + 1 Y_{t+1} Yt+1
三个问题
一旦一个系统可以作为HMM描述,就可以用来解决三个基本问题。
- 评估(Evaluation)
给定HMM,即 μ = [ π , A , B ] \mu = [\pi,A,B] μ=[π,A,B],求某个观测序列的概率.
例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。求第一天湿度为 1,第二天湿度为 2,第三天湿度为 3 的概率。 - 解码(Decoding)
给定HMM,即 μ = [ π , A , B ] \mu = [\pi,A,B] μ=[π,A,B],以及某个观测序列,求得天气的序列。
例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。并且已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得这三天的天气情况
即:发现“最优”状态序列能够“最好地解释”观察序列 - 学习(Learning)
给定一个观察序列,得到一个隐马尔可夫模型。
例如:已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得一个天气的隐马尔可夫模型,包括第一天的天气,天气转移概率矩阵,特定天气下树叶的湿度概率分布。
前向算法
对于评估问题
给定HMM ,求某个序列 μ = [ π , A , B ] \mu = [\pi,A,B] μ=[π,A,B]的观测概率。
例如:给定一个天气的隐马尔可夫模型,包括第一天的天气概率分布,天气转移概率矩阵,特定天气下树叶的湿度概率分布。求第一天湿度为 1,第二天湿度为 2,第三天湿度为 3 的概率。
思路一:找到所有状态序列,得到各状态概率,得到每种状态概率对应的观察概率,求和。
(所有状态序列 → \rightarrow →各状态概率 → \rightarrow →每种状态概率对应的观察概率。 → \rightarrow →求和.


思路二: 采用动态规划——前向算法



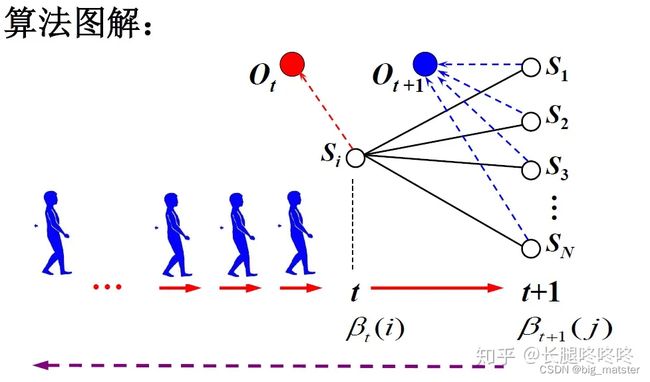
后向算法
Viterbi搜索算法
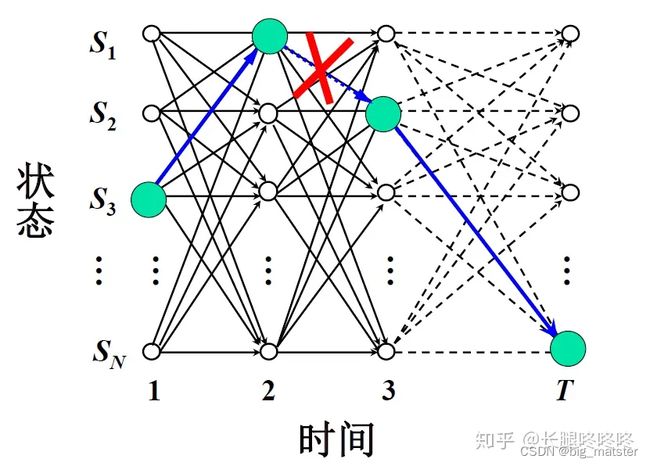
如何理解最优的状态 序列?
Viterbi搜索算法
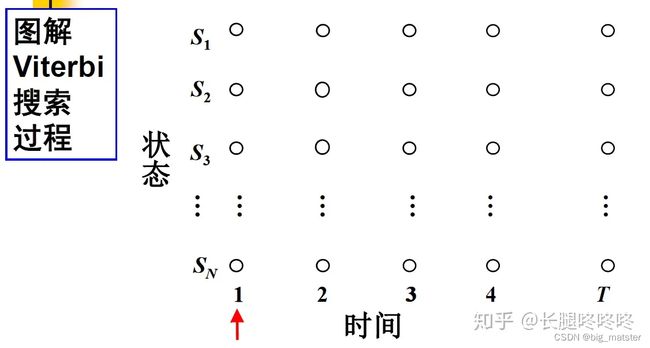
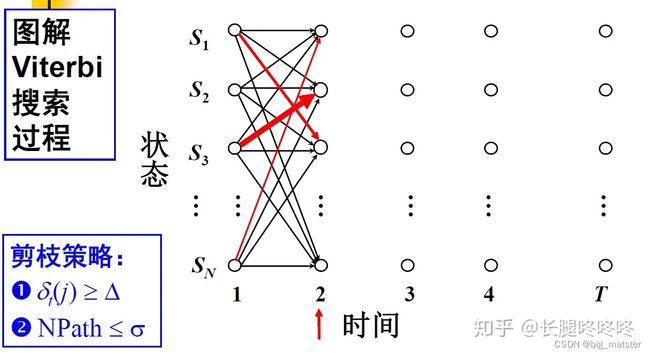


每个时刻都求得每个状态的概率,并求得最大概率对应上一时刻的状态。
算法描述
参数学习
对于学习问题
-
给定一个观察序列,得到一个隐马尔可夫模型。
-
已知第一天湿度为 1,第二天湿度为 2,第三天湿度为 3。求得一个天气的隐马尔可夫模型,包括第一天的天气,天气转移概率矩阵,特定天气下树叶的湿度概率分布。
-
如果产生观察序列 O 的状态已知(即存在大量标注的样本), 可以用最大似然估计来计算 的参数:Baum-Welch 算法(前向后向算法)描述
-
如果不存在大量标注的样本:期望值最大化算法(Expectation-Maximization, EM)
HMM应用
中文分词问题
如果有标注语料,则问题的解决过程:
计算初始状态概率分布
计算转移概率矩阵
计算输出概率矩阵
使用 Viterbi 算法解码
如果没有标注语料,则问题的解决过程:
获取词的个数
确定状态的个数
参数学习(利用 EM 迭代算法获取初始状态概率、状态转移概率和输出概率)
使用 Viterbi 算法解码
学习心得
本次学习就到这里,慢慢的根据应用将隐马尔可夫模型学习到这里,
会使用什么模型,用什么模型都行啦的样子与打算,全部将其搞定都行啦的理由与样子。