时空图卷积网络：一种用于交通预测的深度学习框架

由于交通流的高度非线性和复杂性，传统方法不能满足中长期预测任务的要求，其往往忽略了空间和时间依赖性。在本文中，我们提出了一种新的深度学习框架，时空图卷积网络（STGCN），以解决交通领域的时间序列预测问题（即交通预测）。我们不使用正则卷积和循环单元，而是在图上描述问题，并建立具有完整卷积结构的模型，这使得训练速度更快，参数更少。该体系结构包括几个时空卷积块，它们是图形卷积层和卷积序列学习层的组合，用于建模空间和时间依赖性。这在交通研究中首次应用纯卷积结构从图形结构的时间序列中同时提取时空特征。

交通研究中，交通流的基本变量，即速度、交通量和密度，通常被选为监测交通状况的当前状态的和预测未来的指标。根据预测的长度，交通预测通常分为两个尺度：短期（5∼ 30分钟），中长期（超过30分钟）。大多数流行的统计方法（例如，线性回归）都能很好地进行短期预测。然而，由于交通流的不确定性和复杂性，这些方法对于相对长期的预测效果较差。

之前的中长期交通预测研究大致可以分为两类：动态建模和数据驱动方法。动态建模：使用数学工具（如微分方程）和物理知识，通过计算模拟来描述交通问题。为了达到稳定状态，模拟过程不仅需要复杂的系统编程，还需要消耗大量的计算能力。型中不切实际的假设和简化也会降低预测精度。因此，随着交通数据收集和存储技术的快速发展，大量研究人员将注意力转移到数据驱动的方法上。

经典统计模型和机器学习模型是数据驱动方法的两个主要代表。时间序列分析中，ARIMA及其变体是基于经典统计学的最综合的方法之一。受到时间序列平稳假设的限制，也没有考虑时空相关性。因此，这些方法对于高度非线性交通流的表达性受限。近年来，经典统计模型在交通预测任务中受到了机器学习方法的有力挑战。这些模型，如k近邻算法（KNN）、支持向量机（SVM）和神经网络（NN），可以实现更高的预测精度和更复杂的数据建模。近年深度学习相关工作取得了重大进展，但这些密集网络很难从输入中联合提取时空特征，此外，在狭隘的限制甚至完全没有空间属性的情况下，这些网络的代表能力将受到严重阻碍。

为了充分利用空间特征，使用卷积神经网络（CNN）捕捉交通网络之间的相邻关系，同时在时间轴上使用递归神经网络（RNN）。用于序列学习的循环网络需要迭代训练，这将逐步引入误差累积。此外，基于RNN的网络（包括LSTM）众所周知难以训练且计算量大。

为了克服这些问题，我们引入了几种策略来有效地建模交通流的时间动态和空间依赖性。为了充分利用空间信息，我们通过一个通用图来建模交通网络，而不是单独处理它（例如网格或线段）。为了解决递归网络的固有缺陷，我们在时间轴上采用了完全卷积结构。

交通量预测是一个典型的时间序列预测问题，即给定之前的M个交通量观测值，预测下一个H时间步中最可能的交通量测量值（例如速度或交通流）。

其中，是在时间步t的n个路段的观测向量，其每个元素记录了单个路段的历史观测。在这项工作中，我们定义了一个图上的交通网络，重点关注结构化的交通时间序列。观测值vt不是独立的，而是在图中成对连接。

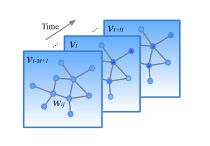图结构的交通数据。每个vt代表时间t上当前交通状态的一个帧，该帧记录在图结构数据矩阵中。vt可以看作是在带权wij的图G上定义的图信号。在第t时间步，在图中，Vt是有限顶点集，对应于交通网络中n个监测站的观测值。代表Gt的带权邻接矩阵。

图上的卷积

基于谱图卷积的概念，我们引入了图卷积算子的概念，作为信号与核Θ的乘积。

其中图傅里叶基是归一化图拉普拉斯（）的特征向量矩阵。是L的特征值的对角矩阵。根据这一定义，图形信号x被内核Θ用Θ与图形傅里叶变换之间相乘进行过滤。

本文所提模型

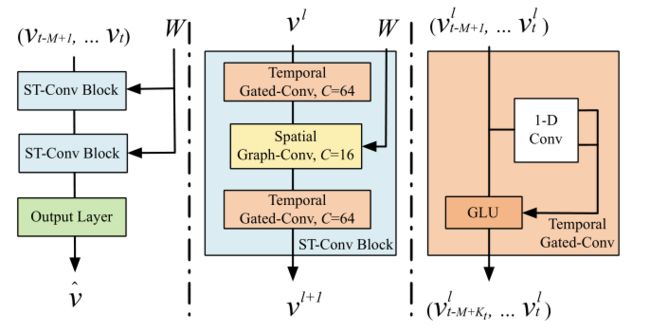
网络架构，将详细介绍提出的时空图卷积网络（STGCN）的架构。STGCN由几个时空卷积块组成，每个时空卷积块形成一个“三明治”结构，两个门控序列卷积层和中间一个空间图卷积层

 时空图卷积网络的体系结构。STGCN框架由两个时空卷积块（ST-Conv块）和最后一个全连接的输出层组成（左）。每个ST-Conv块包含两个时间门控卷积层和中间的一个空间图卷积层（中）。在每个块内部有应用残余连接和瓶颈策略。输入被ST-Conv块统一处理，来连贯的探索空间和时间依赖关系。综合特征由输出层集成，以生成最终预测ˆv。

图卷积网络用于提取空间特征。

交通网络通常组织为图结构，用数学方法将道路网络表示为图。之前的研究忽略了交通网络的空间属性：网络的连通性和全局性被忽略，因为它们被分割成多个段或网格。我们的模型中，图卷积直接用于图结构数据，以提取空间域中具有高度意义的模式和特征。由于图的Fourier基的O（n2）复杂度乘法，公式（2）计算图卷积中的核Θ可能会很昂贵，有两种近似策略用于克服这个问题。

 切比雪夫多项式逼近

使滤波器局部化并减少参数数量，核Θ可以被限制为Λ的多项式，其中是多项式系数向量。K是图卷积的核大小，它决定了从中心节点的最大卷积半径。传统上，切比雪夫多项式被用来将核近似为K-1阶的截断展开，其中缩放的λmax代表L的最大特征值。图卷积可以重新写为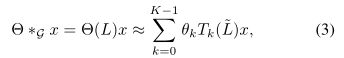其中是在缩放的拉普拉斯下计算的k阶切比雪夫多项式。通过多项式逼近来递归的计算K局部卷积

一阶近似

分层线性公式可以通过堆叠多个带有图拉普拉斯一阶近似的局部图卷积层来定义。更深层次的体系结构可以被构建来恢复深层空间信息。由于神经网络中的缩放和归一化，我们可以进一步假设λmax≈ 2.，因此式3可以被简化成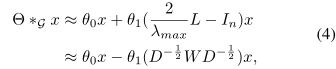其中 是两个核共享参数，为了约束参数和稳定数值性能，可以被一个参数替代，设。W和D是重整后的，即，因此图卷积可以表示为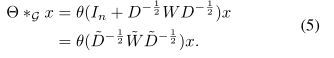

在垂直方向上应用一阶近似的图卷积堆栈，获得与K局部卷积水平方向相似的效果，所有这些卷积都利用了来自中心节点的（K−1）阶邻域的信息，在这种情况下，K是模型中连续过滤操作或卷积层的数量。此外，分层线性结构对于大型图来说是参数经济且高效的，因为近似的阶数仅限于一

 图卷积的推广

 定义在上图卷积算子可以拓展到多维张量。比如对于有Ci个通道的信号，图卷积可以通过拓展，其中有个切比雪夫系数向量（Ci和Co分别是输入和输出的特征大小）。二维变量的图卷积有具体来说，交通预测的输入由M帧道路图组成，每一帧vt都可以看作一个矩阵，其列i是在图Gt在第i个节点的vt的Ci维的值，表示为。对于每个时间步t（总共M个时间步），将具有相同核Θ的等图卷积运算并行施加于。因此，图卷积可以进一步推广到三维变量中有

用于提取时间特征的门控CNN

基于RNN的模型在时间序列分析中得到了广泛应用，但用于交通预测的循环网络仍然存在耗时的迭代、复杂的门机制以及对动态变化的缓慢响应等问题。相反，CNN具有训练速度快、结构简单、与之前步骤没有依赖性约束的优势。我们采用时间轴上的整个卷积结构来捕捉交通流的时间动态行为。这种特殊的设计允许通过多层卷积结构形成分层表示，从而实现并行和可控的训练过程。

时间卷积层含一个带有宽度为Kt的核的1-D因果卷积，后跟门控线性单元（GLU）作为非线性（右）。对于图G中的每个节点，时间卷积在没有填充的情况下探索输入元素的Kt个邻居，导致每次将序列长度缩短Kt-1。每个节点的时间卷积输入可以被视为一个长度为M带有Ci个通道的序列，

，卷积核将输入Y映射为一个单一输出元素

，P，Q被一分为二，通道大小相同，最后，时间门通卷积可以定义为

P、Q分别为GLU中的门输入；元素级Hadamard积。sigmoid门σ（Q）控制当前状态的哪些输入P与发现时间序列中的成分结构和动态方差有关。非线性门也有助于通过堆叠的时间层利用完整的输入场。此外，在堆叠的时间卷积层之间实现残余连接。同样，通过对每个节点使用相同的卷积核Γ，时间卷积也可以推广到三维变量，表示为

时空卷积块

为了融合时空域的特征，构造时空卷积块（ST Conv块）来联合处理图形结构的时间序列。根据特定情况的规模和复杂性，区块本身可以堆叠或延伸。中间的空间层是连接两个时间层的桥梁，可以实现从通过时间卷积的来自图卷积的快速空间状态传播（中）。“三明治”结构还有助于网络充分应用瓶颈策略，通过图卷积层对通道C进行降尺度和升尺度，实现尺度压缩和特征压缩。此外，在每个ST-Conv块中使用层标准化来防止过度拟合。

ST Conv块的输入和输出都是三维张量。块l的输入，输出

由计算，其中是块l中的上下时间核，是图卷积空间核。ReLU（·）表示校正后的线性单位函数。在堆叠两个ST Conv块后，我们附加一个额外的时间卷积层，其带有一个全连接的层作为最后的输出层（左）。时间卷积层将最后一个ST Conv块的输出映射到一个单步预测。然后，我们可以得到最终的输出，通过跨c通道应用线性变换，计算n个节点的速度预测，即 w是权重向量，b是偏差。我们使用L2损失来衡量模型的性能。因此，用于交通预测的STGCN损失函数可以写成

代表模型的预测，是真实值，是模型所有可学习参数

总结：STGCN是处理结构化时间序列的通用框架，可处理一般的时空序列学习任务。时空块结合了图卷积和门控时间卷积，可以提取空间特征，并连贯地捕获时间特征。模型完全由卷积结构组成，因此能够以较少的参数和较快的训练速度实现对输入的并行化。