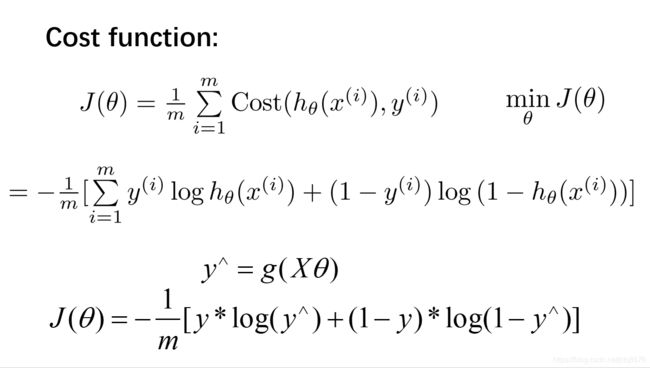逻辑回归之线性可分
文章目录
-
-
-
-
- 公式推导
-
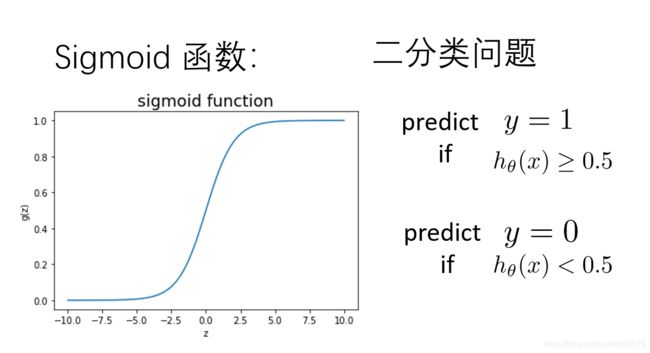
- 1.Sigmoid函数
- 2.损失函数
- 3. 梯度下降函数
- 代码实现
-
-
-
逻辑回归-线性不可分案例
案例:设想你是工厂的生产主管,你要决定是否芯片要被接受或抛弃
数据集:ex2data2.txt,芯片在两次测试中的测试结果
公式推导
站在巨人的肩膀上
1.Sigmoid函数
2.损失函数
3. 梯度下降函数
代码实现
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex2data1.txt'
data = pd.read_csv(path, names=['Exam1', 'Exam2', 'Accepted'])
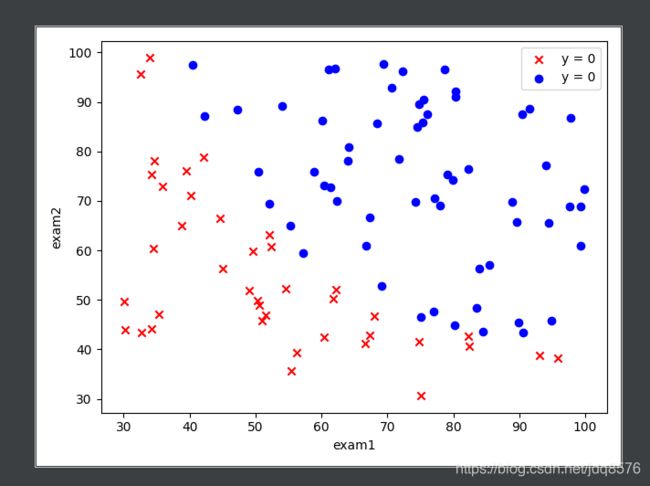
fig, ax = plt.subplots()
ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r',
marker='x', label='y = 0')
ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='b',
marker='o', label='y = 0')
ax.legend()
ax.set(xlabel='exam1', ylabel='exam2')
plt.show()
def get_Xy(data):
'''
处理原始数据,变成我们想要的
:param data:前期从文件中读取的data数据
:return: 返回特征矩阵和标签矩阵
'''
data.insert(0, 'ones', 1)
X_ = data.iloc[:, 0:-1]
X = X_.values
y_ = data.iloc[:, -1]
y = y_.values.reshape(len(y_), 1)
return X, y
X, y = get_Xy(data)
def sigmoid(z):
"""
实现sigmoid函数
:param z:
:return:
"""
return 1 / (1 + np.exp(-z))
def costFunction(X, y, theta):
"""
损失函数
:param X:特征值
:param y: 标签值
:param theta: 参数
:return:
"""
A = sigmoid(X.dot(theta))
first = y * np.log(A)
second = (1 - y) * np.log(1 - A)
return -np.sum(first + second) / len(X)
# 生产原始参数
theta = np.zeros((3, 1))
def gradientDescent(X, y, theta, iters, alpha):
m = len(X)
costs = []
for i in range(iters):
A = sigmoid(X.dot(theta))
theta = theta - alpha / m * X.T.dot(A - y)
cost = costFunction(X, y, theta)
costs.append(cost)
if i % 1000 == 0:
print(cost)
return costs, theta
# 步长
alpha = 0.004
# 迭代次数
iters = 200000
# 梯度下降法拟合参数theta,并求出损失函数的值
costs, theta_final = gradientDescent(X, y, theta, iters, alpha)
print(theta_final)
'''Output值
[[-23.77361748]
[ 0.18688137]
[ 0.18042754]]
'''
def predict(X, theta):
"""
根据我们拟合出的theta值去预判y的值,并返回
:param X: 特征矩阵
:param theta: 拟合参数theta
:return: 返回根据拟合参数进行预判的y值
"""
prob = sigmoid(X.dot(theta))
return [1 if x >= 0.5 else 0 for x in prob]
y_ = np.array(predict(X, theta_final))
y_pre = y_.reshape(len(y_), 1)
acc = np.mean(y == y_pre)
print(acc) # 0.86
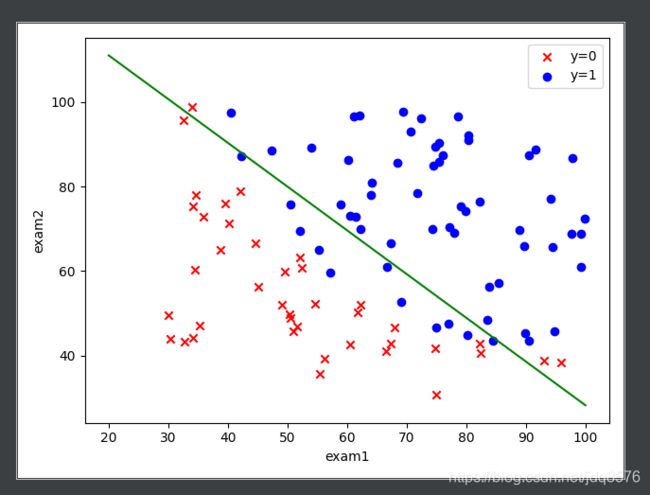
# 画出拟合直线
coef1 = - theta_final[0, 0] / theta_final[2, 0]
coef2 = - theta_final[1, 0] / theta_final[2, 0]
x = np.linspace(20, 100, 100)
f = coef1 + coef2 * x
fig, ax = plt.subplots()
ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r', marker='x', label='y=0')
ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='b', marker='o', label='y=1')
ax.legend()
ax.set(xlabel='exam1',
ylabel='exam2')
ax.plot(x, f, c='g')
plt.show()