【数据挖掘】数据预处理

Outline

Chapter	Overview
1.	为什么要对数据预处理
2.	数据描述性总结
3.	数据清洗
4.	数据变换
5.	数据整合
6.	数据归约
7.	离散化与概念层级
8.	总结

---

Chapter 1. 为什么要预处理

我们从现实生活中获得的原始数据，或多或少会因为各种原因不能直接使用。例如：

• 不完整
  • 收集时的“不适用”数据值
  • 收集数据的时间和分析数据的时间之间的不同考虑
  • 人力/硬件/软件问题
• 噪声
  • 数据采集仪器故障
  • 数据输入时的人为或计算机错误
  • 数据传输错误
• 格式不一致
  • 不同的数据源
  • 不同规格的采集方式和标准
• 重复数据

数据的质量决定了数据挖掘的质量

---

数据预处理的主要任务

Tasks	Conception
数据清洗	填充缺失值、平滑噪声、识别离群点、解决不一致
数据整合	多个不同来源的数据聚合
数据变换	标准化和聚集
数据归约	减少数据量，但保留主要信息
数据离散化	对连续的数值数据进行离散化

---

Chapter 2. 数据描述性总结

中心趋势度

指的是一组数据向某一中心值靠拢的程度，反映了一组数据的中心点所在。

1️⃣ 均值

最常见的统计量，可以表征数据的总体水平。但均值对于噪声比较敏感。

2️⃣ 中位数

先排序，再找中心。毫无疑问，这个方法的时间开销至少是$O(nlo{g}_n)$级别的。所以有时候，我们可以采用近似估计的方式去计算。

假定数据可以通过数值划分为区间，且知道每个区间的个数。于是，中位数可用以下的公式表示。
$$median=L_1+\left[\frac{\frac{N}{2}-(\sum f{)}_l}{f_{median}}\right]width$$
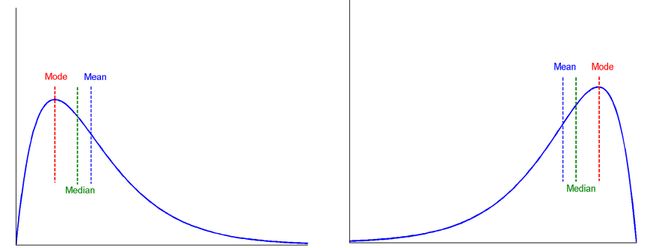
3️⃣ 众数

众数是一组数据中出现最多的数值，有多少个众数，那么我们称数据集为多少峰，例如一个众数：单峰，两个：双峰。

4️⃣ 中列数

Midrange，表示最大值和最小值的均值。也可以度量中心趋势哦。不过与其说度量中心，倒不如说是数据范围的中心，正如mid和range的意思一般。

尾巴往哪甩，数据往哪偏

---

离散趋势度

用于评估数据的散布或发散程度。

1️⃣ 极差、四分位数和四分位数极差

极差(Range)也称范围误差或者全距，指的是最大值和最小值的差距。也是衡量变动最简单的指标。

四分位数：将数据从大到小排序后，用三个点(25,50,75)将数据分为三等分，这三个点上对应的位置就是四分位数。例如$Q_1,Q_2,Q_3$表示第一四分位数，第二四分位数，第三四分位数。

分半四分位差：即$(Q_3-Q_1)/2$

四分位数极差(IQR)：$Q_3-Q_1$，它给出了数据中间一半的部分。

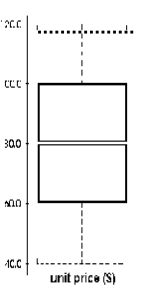
2️⃣ 五数概括、盒图和离群点

哪五个数？

• min
• $Q_1$
• $Q_2$
• $Q_3$
• max

从下往上分别是：最小值、Q1、中位数、Q3、最大值

盒图又称箱线图，盒须图，体现了五数概括。利用四分位数间距$IQR$，我们可以判断界限，找出异常值。通常设定1.5倍$IQR$外的为异常值。所以边界为：
$$\begin{gathered} IQ{R}_{左}=Q_1-1.5\times IQR \\ IQ{R}_{右}=Q_3+1.5\times IQR \end{gathered}$$

---

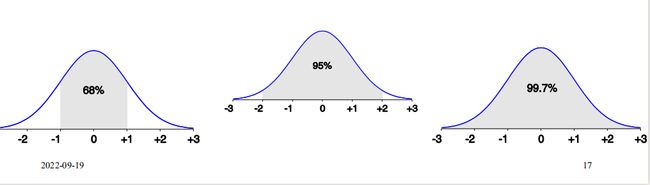
正态分布曲线

• 区间$[\mu \pm \sigma ]$有$68\%$的数据量
• 区间$[\mu \pm 2\sigma ]$有$95\%$的数据量
• 区间$[\mu \pm 3\sigma ]$有$99.7\%$的数据量，超过此区间的数据，我们就可以将其视作离群点了(小概率事件)

---

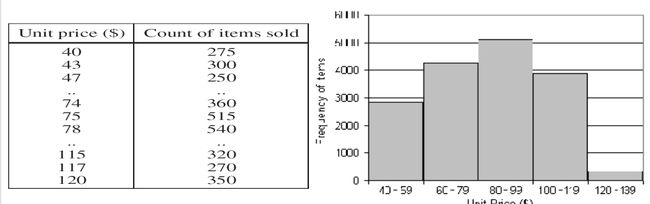
直方图分析

直方图方便我们观察数据的分布情况

---

QQ图 Quantile-Quantile Plot

QQPlot图是用于直观验证一组数据是否来自某个分布，或者验证某两组数据是否来自同一（族）分布。在教学和软件中常用的是检验数据是否来自于正态分布。

公式描述为：
$$f_i=\frac{i-0.5}{n}$$
对于一组递增排序的数据$X$，$f_i$表示有$100\%f_i$的数据小于或等于$x_i$。

一般来说，横坐标为实际分位数，纵坐标为标准分布，若QQ图的点分布在y=x曲线附近，说明数据近似正态分布。

---

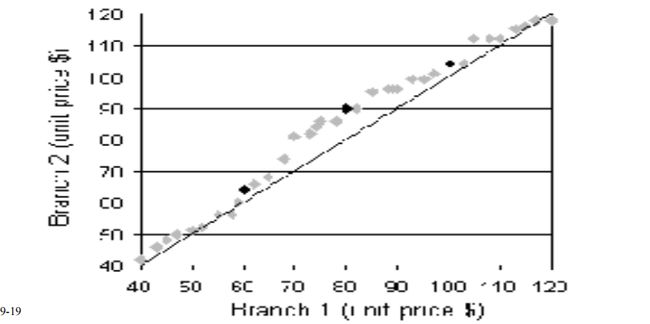
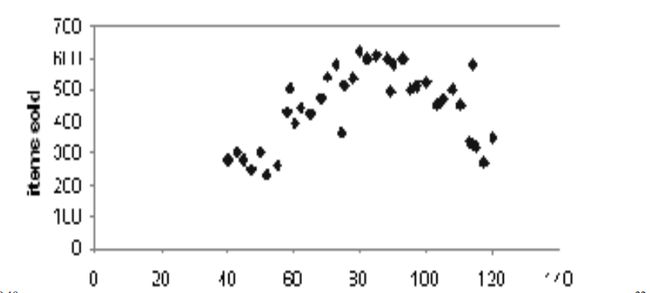
散点图

一般是二维或者三维散点图，用来查看数据的聚类、离群点，或是两个特征之间的相关性。

---

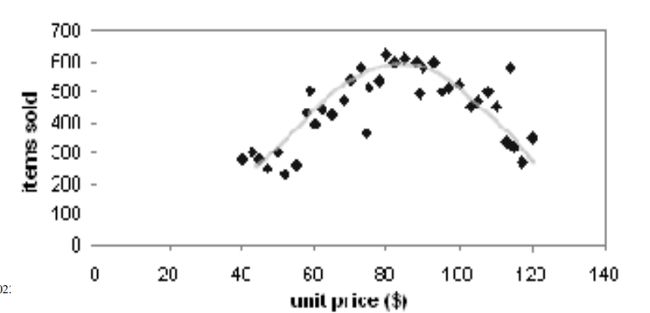
路易斯曲线 Loess Curve

在散点图中增加一条曲线，用来拟合回归数据的

---

Chapter 3. 数据清洗

数据清洗可以说是数据仓库中的核心问题

数据清洗的主要任务

Tasks
填充缺失值
识别异常值和平滑噪声
纠正不一致的数据
解决冗余问题

1️⃣ 缺失值

常见处理手段有：

• 忽略该数据，通常在某些关键数据缺失(比如分类时的label标签缺失)时进行
• 填充缺失值
  • 基于统计信息
  • 基于推理信息，如贝叶斯、决策树
  • 基于各种模型

2️⃣ 噪声

在一个被测量的变量中的随机误差或方差

噪声一般来说是数据中的随机误差，当然，不一致或者重复的数据也可也算作噪声。

常见的处理手段有：

• Binning
  • 将数据排序后分组(bins)
  • 按照各个组的中值、边缘等对噪声进行平滑处理
• 回归
  • 通过回归函数平滑噪声
• 聚类
  • 检测和移除离群点
• 计算机结合人类
  • 单走一个6

Binning算法可以分为等距离划分和等频率划分：

等距离	等频率
也叫等宽度(Equal-width)	也叫等深度(Equal-depth)
将数据划分为N个宽度相同的间隔	将数据划分为N个元素数量相同的间隔
每个间隔的大小为：$(Max-Min)/n$	每个间隔的元素大小为：$All/n$
容易受到异常影响！且稀疏数据很难处理	具有良好的数据缩放

我们举个binning的栗子

假设有这样一组数据：

age	23	23	27	27	39	41	47	49	50	52	54	54	56	57	58	58	60	61
%fat	9.5	26.5	7.8	17.8	31.4	25.9	27.4	27.2	31.2	34.6	42.5	28.8	33.4	30.2	34.1	32.9	41.2	35.7

现在我们要做一个分组为6的边缘平滑：

这里因为我们是对排好序的数据做处理，所以可以通过二分法进行优化，获取中间分界。

def close(x,a,b):
    # 是否靠近下界
    return (x-a)<=(b-x)

def boundary(x):
    Min=x[0]
    Max=x[-1]

    l,r=0,len(x)-1
    while l<=r:
        mid=(r-l)//2+l
        if close(x[mid],Min,Max):
            if not close(x[mid+1],Min,Max):
                l=mid
                break
            l=mid+1
        else:
            if close(x[mid-1],Min,Max):
                l=mid
                break
            r=mid-1
    return [[Min]*l+[Max]*(len(x)-l)]

N_y=sorted(y)
bins=[[]]
for j in N_y:
    bins[-1].append(j)
    if len((v:=bins[-1]))==6:
        v[:]=boundary(v)
        bins.append([])
for i,j  in enumerate(bins[:-1]):
    print("bin %d is :"%(i+1),j)

bin 1 is : [[7.8, 7.8, 27.2, 27.2, 27.2, 27.2]]
bin 2 is : [[27.4, 27.4, 32.9, 32.9, 32.9, 32.9]]
bin 3 is : [[33.4, 33.4, 33.4, 33.4, 42.5, 42.5]]

---

Chapter 4. 数据变换

数据变换的工作主要是让数据满足某一规则，比如都在某一区间，比如映射到频域等。

主要的工作有：

Tasks	Description
平滑	移除噪声
标准化	缩放区间
聚合	数据立方体构建
属性/特征构造	也就是构建新特征

常见数据标准化

1️⃣ 最大最小标准化
$$v^{\prime }=\frac{v-mi{n}_i}{ma{x}_i-mi{n}_i}$$
2️⃣ Z得分标准化
$$v^{\prime }=\frac{v-\mu }{\sigma }$$
其中：
$$\mu =\frac{\sum v}{n}$$

$$\sigma =\frac{\sum |v-\mu |}{n}$$

3️⃣ 十进制缩放
$$v^{\prime }=\frac{v}{10^j}$$

---

Chapter 5. 数据集成

这个部分关注的重点有：

• 多源数据集成
• 同一个数据在不同源上的表现
• 检测和识别数据冲突
• 数据冗余

如何解决数据冗余？

冗余的数据很多时候都是由另一个属性派生出来的

所以，我们可以通过相关性检测来识别。

1️⃣ 协方差

对于数值型数据，我们可以计算他的协方差：
$$r_{A,B}=\frac{\sum (a_i-\bar{A})(b_i-\bar{B})}{(n-1){\sigma }_A{\sigma }_B}=\frac{\sum (a_i{b}_i)-n\bar{A}\bar{B}}{(n-1){\sigma }_A{\sigma }_B}$$

$r>0$表示正相关，$r<0$表示负相关

2️⃣ *${\chi }^2$检验

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。

卡方检验适用于标称属性，假设对于两个属性$A,B$,$A$有$c$个不同的取值，$B$有$r$个不同的取值，用$A$和$B$描述的数据元组可以用一个相依表显示，其中$A$的$c$个值构成列，$B$的$r$个值构成行。$(A_i,B_j)$表示属性$A$取$i$，属性$B$取$j$的联合事件。
$${\chi }^2=\sum _{i=1}^c\sum _{j=1}^c\frac{(o_{ij}-e_{ij}{)}^2}{e_{ij}}$$
其中$O_{ij}$表示联合事件的观测频度，$e_{ij}$表示期望频度，计算式为：
$$e_{ij}=\frac{count(A=a_i)\times count(B=b_j)}{n}$$
$n$为元组个数。

例如：

---

Chapter 6. 数据规约

一个数据库或者数据仓库可能可以存储TB级的数据，如果想对这些数据进行分析或者挖掘是十分困难的

数据规约可以获得数据体积小得多，但产生相同（或几乎相同）的分析结果。

常见的策略

Strategies
数据立方体聚合
尺寸减少----移除不重要的属性
数据压缩
数量减少
离散化和概念层次结构的生成

---

1️⃣ 数据立方体

数据立方体的最低级别(基本立方)

• 针对感兴趣的单个实体的聚合数据

数据多维数据集中的多个级别的聚合

• 进一步减小要处理的数据的大小

2️⃣ 特征选择（即属性子集选择）

• 选择一组最小的功能不同类别的概率分布,这些功能的值尽可能接近给定所有特征值的原始分布

• 减少模式中的特征数量，更容易理解

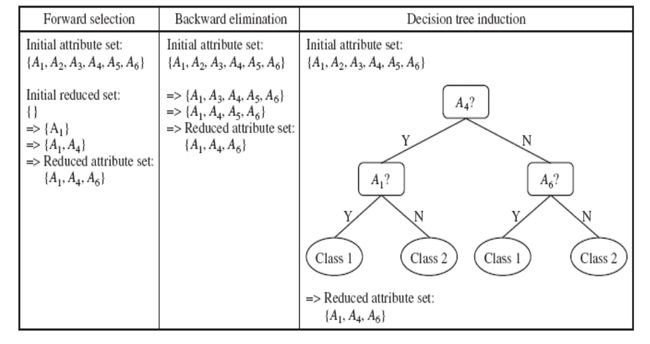
常见的模式：

前项选择、后向选择、决策树归纳

3️⃣ 主成分分析

给定N维的N个数据向量，求k≤ n个最适合用于表示数据的向量（主成分）

步骤

• 规格化输入数据：每个属性都在同一范围内

• 计算k个向量，即主分量

• 每个输入数据（矢量）是k个主分量矢量的线性组合

• 主要成分按“重要性”或强度递减的顺序排序

• 由于对成分进行了排序，因此可以通过消除弱成分（即具有低方差的成分）来减小数据的大小。（即，使用最强的主成分，可以重建原始数据的良好近似值）

仅适用于数字数据

简单来说，就是：

• 去均值(距平)
• 计算协方差矩阵
• 求解协方差矩阵特征值和特征向量
• 按特征值大小排序，将原始数据映射到特征向量上

4️⃣ 数据压缩

字符串压缩

• 有广泛的理论和完善的算法

• 通常是无损的

• 但在没有扩展的情况下，只能进行有限的操作

音频/视频压缩

• 典型的有损压缩，具有渐进式改进

• 有时可以重建信号的小片段而不重建整个

5️⃣ 小波变换

离散小波变换（DWT）：线性信号处理、多分辨率分析

• 压缩近似：仅存储最强小波系数的一小部分

• 类似于离散傅里叶变换（DFT），但更好的有损压缩，局限于空间

方法：

• 长度L必须是2的整数幂（必要时用0填充）

• 每个变换有两个功能：平滑、差异

• 适用于数据对，产生长度为L/2的两组数据

• 递归应用两个函数，直到达到所需长度

6️⃣ 数量减少

通过选择其他更小的数据表示形式来减少数据量

• 参数化方法

  • 假设数据符合某些模型，估计模型参数，仅存储参数，并丢弃数据（可能的异常值除外）

• 非参数方法

  • 直方图、聚类、抽样

7️⃣ 回归模型

8️⃣ 直方图

9️⃣ 聚类

采样

---

Chapter 7. 离散化和概念层级

离散化

• 通过将属性的范围划分为间隔，减少给定连续属性的值数量

• 然后可以使用间隔标签替换实际数据值

• 离散化可以递归地对属性执行

概念层次结构

• 通过收集低级概念（如年龄的数值）并将其替换为高级概念（如年轻人、中年人或老年人），递归地减少数据

在数值型数据上，数据离散化和概念层次生成的经典方法：

• 装箱

  • 自上而下拆分，用二进制平均值或中值替换值

• 直方图分析

  • 自上而下拆分

• 聚类分析

  • 自上而下拆分

• 基于熵的离散化：有监督的、自上而下的分割

• 自然分割：自上而下分割

举个栗子：

1️⃣ 基于熵的离散化

熵是对信息混乱程度的度量，其可以写作：
$$E(s)=-\sum _i^{n}plo{g}_2(p)$$
给定一个样本$S$，将$S$用边界$T$划分为两个连续的区间$S_1$和$S_2$，那么分区后的熵就是：
$$Entropy(S,T)=\frac{|S_1|}{|S|}Entropy(S_1)+\frac{|S_1|}{|S|}Entropy(S_1)$$
在所有的边界中，我们选择信息增益$T$最大的边界作为划分：
$$Gain(S,T)=Entropy(S)-Entropy(S,T)$$
递归执行此过程，这样的边界可以减少数据量，大幅度提高分类精度。

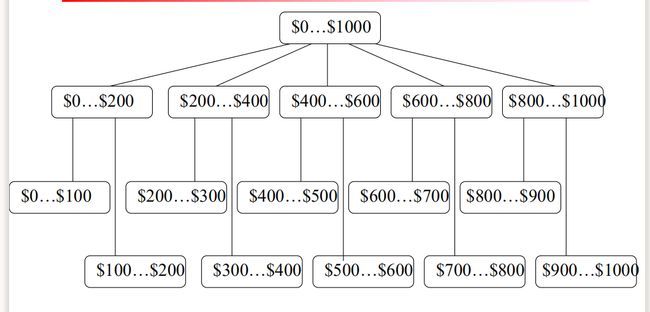
2️⃣ 自然分区分割

可以通过一个简单的$3-4-5$规则对数据进行分割。

• 如果一个区间最高有效位上包含3，6，7或9个 不同的值，就将该区间划分为3个等宽子区间； (为7的话，划分成 2,3,2的宽度比例) ;
• 如果一个区间最高有效位上包含2，4，或8个不 同的值，就将该区间划分为4个等宽子区间；
• 如果一个区间最高有效位上包含1，5，或10个不同的值，就将该区间划分为5个等宽子区间；

将该规则递归的应用于每个子区间，产生给定数值属性的概念分层

先找到Low和High，向上向下找最近的最高位，依此划分作为主体。

下一步进行全数据分析，包含了Min向下和Max向上，只不过如果最小区间包含了最小值，将最小区间的坐区间修正到最小值，并添加主体到最大值的分支。

3️⃣ 针对分类数据的概念层次结构的生成

• 由用户或专家在模式级别上明确说明属性的部分/全部排序
  • street < city < state < country
• 通过显式数据分组指定一组值的层次结构
  • {Urbana, Champaign, Chicago} < llinois
• 通过分析不同值的数量，自动生成层次结构（或属性级别）
  • E.g., for a set of attributes: {street, city, state, country}

4️⃣ 自动的概念层次结构的生成

可以根据分析数据集中每个属性的不同值的数量，自动生成一些层次结构

• 具有最明显值的属性被放置在层次结构的最低级别