【深度学习经典网络架构—7】:MobileNet系列(V1、V2、V3)
✨博客主页:米开朗琪罗~
✨博主爱好:羽毛球
✨年轻人要:Living for the moment(活在当下)!
推荐专栏:【图像处理】【千锤百炼Python】【深度学习】【排序算法】
目录
- 一、简述
- 二、创新点
- 三、传统卷积与深度可分离卷积
- 四、MobileNet V1
- 五、MobileNet V2
-
- 5.1 创新点
- 5.2 Linear Bottlenecks
- 5.3 Inverted Residual Structure
- 5.4 MobileNet V2 Block
- 六、MobileNet V3
一、简述
自从AlexNet赢得ImageNet挑战赛:ILSVRC 2012以来,卷积神经网络已成为计算机视觉中的普遍应用。总体趋势是制作更深、更复杂的网络,以实现更高的准确度。然而,这些提高准确性的进步并不一定会使网络在规模和速度方面更有效率。在机器人、汽车自动驾驶和增强现实等许多现实世界的应用中,识别任务需要在计算受限的平台上及时执行。
谷歌提出MobileNet的目的就是构造一个可以在移动端和嵌入式端应用深度学习的网络,使得在CPU上也能达到理想的速度要求。
MobileNet V1:MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
MobileNet V2:MobileNetV2: Inverted Residuals and Linear Bottlenecks
MobileNet V3:Searching for MobileNetV3
二、创新点
在第一部分简述中说过,现在神经网络的发展已经发生了由大到小的转型,轻量化的神经网络在许多场景中至关重要(例如智能驾驶、智能医疗等)。
轻量化网络的研究是在保证网络性能的前提下,减少模型参数,提升模型速度,具有较强的挂飞能力。
作者引入了Depthwise Separable Convolution(深度可分离卷积),深度可分离卷积可以大大减少计算量与网络参数量!
三、传统卷积与深度可分离卷积
本节将解释为什么深度可分离卷积的参数量要少于传统卷积!
深度可分离卷积是将标准卷积分解成为深度卷积(depthwise convolution)和逐点卷积(pointwise convolution),分解过程如下图所示:

我们用公式说明深度可分离卷积较标准卷积的参数变化情况:
我们设输入特征图的尺寸大小为 ( D F , D F , M ) (D_{F},D_{F},M) (DF,DF,M),标准卷积 K K K为 ( D K , D K , M , N ) (D_{K},D_{K},M,N) (DK,DK,M,N),输出特征图的尺寸大小为 ( D G , D G , N ) (D_{G},D_{G},N) (DG,DG,N),则对于标准卷积,其计算量为:
D K × D K × M × N × D F × D F D_{K}\times D_{K}\times M\times N\times D_{F}\times D_{F} DK×DK×M×N×DF×DF
对于深度卷积Depthwise Convolution来说,其计算量为:
D K × D K × M × D F × D F D_{K}\times D_{K}\times M\times D_{F}\times D_{F} DK×DK×M×DF×DF
对于点卷积Pointwise Convolution来说,其计算量为:
M × N × D F × D F M\times N\times D_{F}\times D_{F} M×N×DF×DF
所以深度可分离卷积的总计算量为:
D K × D K × M × D F × D F + M × N × D F × D F D_{K}\times D_{K}\times M\times D_{F}\times D_{F}+M\times N\times D_{F}\times D_{F} DK×DK×M×DF×DF+M×N×DF×DF
所以深度可分离卷积与标准卷积相比,计算量有明显减少:
D K × D K × M × D F × D F + M × N × D F × D F D K × D K × M × N × D F × D F = 1 N + 1 D K 2 \frac{D_{K}\times D_{K}\times M\times D_{F}\times D_{F}+M\times N\times D_{F}\times D_{F}}{D_{K}\times D_{K}\times M\times N\times D_{F}\times D_{F}}=\frac{1}{N}+\frac{1}{D_{K}^{2}} DK×DK×M×N×DF×DFDK×DK×M×DF×DF+M×N×DF×DF=N1+DK21
四、MobileNet V1
MobileNet V1使用深度可分离卷积替代标准卷积,如下图所示。同时卷积块添加 1 × 1 1×1 1×1的卷积层起滤波与线性组合的作用。

MobileNet V1的具体网络结构如下表所示:
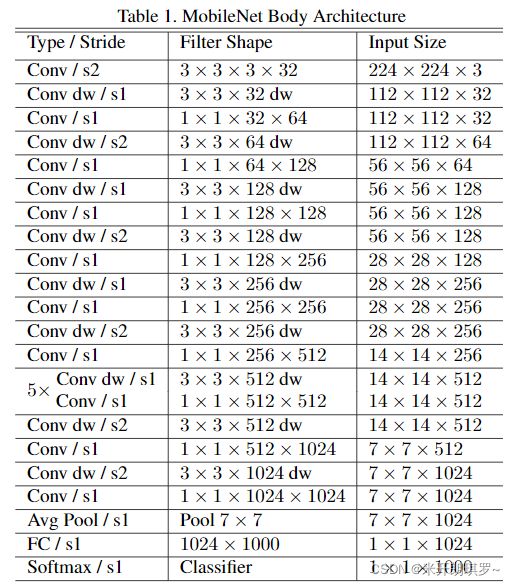
网络通篇是深度可分离卷积与 1 × 1 1×1 1×1的卷积层的串联结构,并且除了全连接层外,所有的卷积层都补充了BN层和ReLU激活函数。
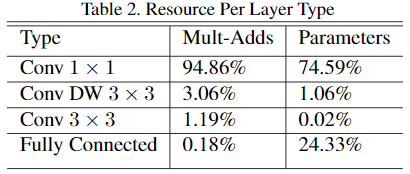
作者将几乎所有的密集运算集中到 1 × 1 1×1 1×1上,这样作者可以使用高度优化的矩阵乘法 general matrix multiply(GEMM) 计算。
在MobileNet中有95%的时间花费在 1 × 1 1×1 1×1上,这部分参数的占比也接近75%。
五、MobileNet V2
为了进一步提高模型的移植能力及先进性能,作者深入到网络的底层,重新思考网络各部分的效能及优化方式,从而推出了MobileNet V2。
5.1 创新点
作者论文的标题就是MobileNet V2的创新点:
- Linear Bottlenecks(线性瓶颈):对MobileNet V2的Block的最后一个 1 × 1 1×1 1×1卷积层激活函数做出改变,使用Linear激活函数替代ReLU。
- Inverted Residual Structure(倒转残差结构):与传统的卷积块对特征图的升维、降维不同,Inverted Residual Structure先将特征图扩展到高维,然后再通过卷积降维。
5.2 Linear Bottlenecks
长期以来,人们一直认为神经网络中感兴趣的流形(manifold of interest)可以嵌入低维子空间。这样的事实可以通过简单地降低层的维度从而降低操作空间的维度来捕捉和利用。
MobileNet V1已经成功地利用了这一点,通过一个宽度乘数参数(width multiplier parameter),有效地在计算和精度之间进行了权衡,并将其纳入了其他网络的高效模型设计中。因此,宽度乘数方法可以降低激活空间的维数,直到感兴趣的流形跨越整个空间。
如果空间内的感兴趣的流行具有较高的完整度,则经过ReLU后,很可能会使得激活空间崩溃,不可避免的会丢失信息。作者指出:如果输入流形可以嵌入到激活空间的一个低维子空间中,那么ReLU变换可以保留信息,同时将所需的复杂性引入可表达函数集。
下图为嵌入高维空间的低维流形的ReLU变换示例。图中使用随机矩阵T和ReLU将初始螺旋嵌入n维空间,然后使用 T − 1 T^{-1} T−1将其投影回2D空间。在上面的例子中,n=2和3导致信息丢失,其中流形的某些点彼此塌陷,而对于n=15到30,变换是高度非凸的。

总之:感兴趣的流形应该位于高维激活空间的低维子空间中:
既然在低维空间中使用ReLU做激活变换会丢失很多信息,因此论文使用Linear Bottleneck取代ReLU激活。
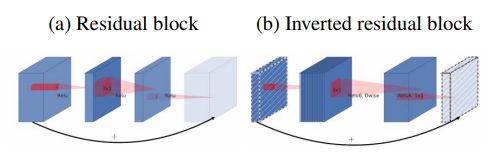
- 图a展示的是标准卷积,标准卷积将空间和通道信息一起映射到下一层,参数和计算量会比较大;
- 图b展示的是可分离卷积,深度卷积负责逐通道的过滤空间信息,逐点卷积负责映射通道;
- 图c和图d是MobileNet V2的核心组成结构(d是c的下一个连接状态),不同于图b的是,在逐点卷积后使用了接 1 × 1 1×1 1×1卷积,该卷积使用线性变换,总称为一层低维linear bottleneck,其作用是将输入映射回低维空间。
5.3 Inverted Residual Structure
因为在5.2中我们阐述了实际上linear bottleneck基本包含了所有的必要信息,所以在构造Inverted Residual Structure时,跳跃连接选择放在linear bottleneck之前,而不是其他网络层,如下图所示。
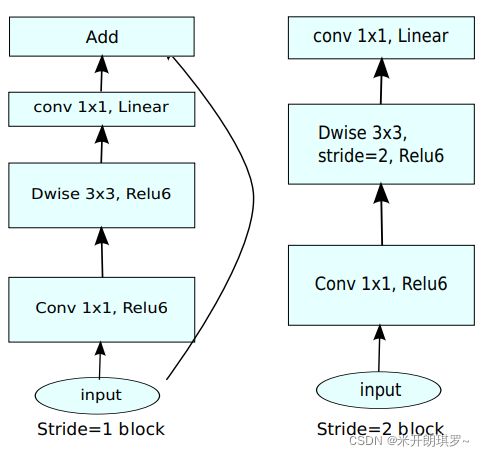
下图Bottleneck residual block的结构表示:
- 首先使用 1 × 1 1×1 1×1卷积变换通道,然后使用ReLU6激活神经元;
- 中间使用深度卷积,同样使用ReLU6激活神经元;
- 最后使用 1 × 1 1×1 1×1卷积变换通道,但在这里不使用ReLU,而是使用Linear激活。

5.4 MobileNet V2 Block
下图是MobileNet V2的Block结构,其中方块的高度表示通道数,可以看出MobileNet V2对特征图是先扩张再压缩。
六、MobileNet V3
MobileNet V3发表于2019年,是MobileNet家族的又一大作,V3不仅充分使用了V1的深度可分离卷积与V2的Linear Bottlenecks、Inverted Residual Structure,而且结合了注意力模块Se_Block,并利用NAS(神经结构搜索)搜索网络配置与参数。
关于MobileNet V3的更多讲解请参考:
轻量化网络:MobileNet v3解析
mobilenet系列之又一新成员—mobilenet-v3
