【Abee】吃掉西瓜——西瓜书学习笔记（四）

神经网络（neural networks）

 

目录

【内容包含 第五章】

神经元模型

感知器与多层网络

多层前馈神经网络（multi-layer feedforward neural networks）

反向传播算法（error BackPropagation，BP）

BP算法解决过拟合的问题

全局最小（global minimum）与局部极小（local minimum）

其他常见神经网络

深度学习（deep learning）

---

 

神经元模型

通过n个其他神经元传过来的信号，加上权重，当前神经元的阈值进行比较，通过激活函数（activation function）处理，再输出。

激活函数一般使用Sigmoid函数，和阶跃函数相比，它连续、光滑。

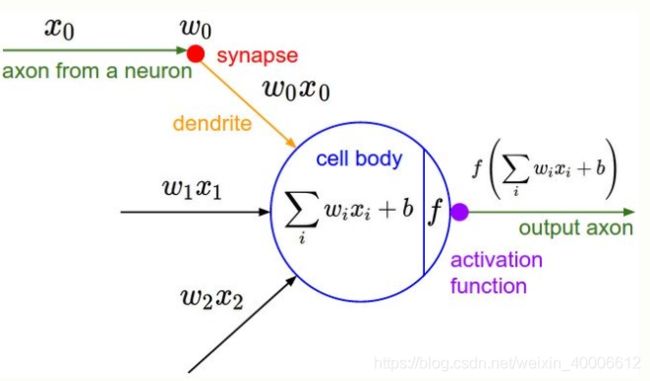图1 神经元模型 图片来源 图2 Sigmoid函数 图片来源

 

---

感知器与多层网络

感知器（Perceptron）由两层神经元组成，输出层为M-P神经元，也称 阈值逻辑单元（threshold logic unit）

感知器

 

输出层为

                                                                           

权重，均可训练，具体操作为

                                                                                

                                                                              

其中是学习率（learning rate）

已被证明，如果两类模型是线性可分的，那么感知器的学习一定会收敛。

如果需要解决非线性可分问题，需要采用多层功能神经元，输入层与输出层之间存在隐含层（hidden layer），隐含层和输出层神经元都是拥有激活函数的功能神经元。

 

---

多层前馈神经网络（multi-layer feedforward neural networks）

每层神经元与下一层神经元全互连，不存在同层连接也不存在跨层连接的神经网络

图3 多层前馈神经网络 

 

---

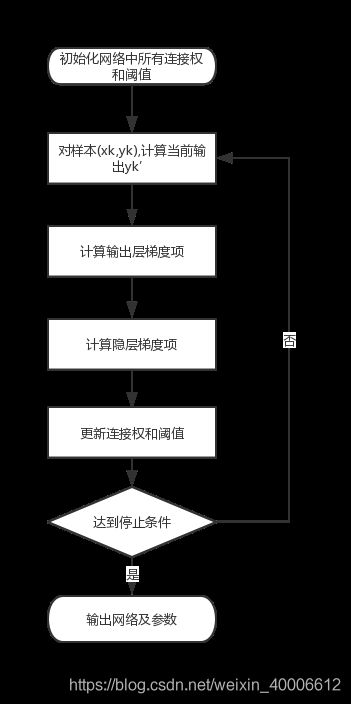
反向传播算法（error BackPropagation，BP）

BP可以用于多种类型的神经网络，是迄今为止最成功的的神经网络学习算法，一般指的BP神经网络是指用BP算法训练的多层前馈神经网络

假设存在d个输入，一层隐层q个神经元，l个输出，则需要训练的参数有  个参数，前两个为权值，后两个为阈值。BP是一个迭代学习算法，在迭代每一轮中采用广义的感知器学习规则进行参数更新

                                                                                          

BP算法基于 梯度下降（gradient descent）策略，误差选择均方误差，给定学习率

                                                                                   

                                                                                       

两层BP神经网络（单隐层）训练流程

上图所示的是两层BP神经网络的“标准算法”，误差为单个,还有 累计误差反向传播（accumulated error backpropagation），取得误差为训练集上的累积误差。

已有文献证明，一个包含足够多神经元的隐层的多层前馈网络可以以任意精度逼近任意复杂度的连续函数。

 

---

BP算法解决过拟合的问题

早停（early stopping）

若训练集误差降低而验证集误差升高，则停止训练，并返回最小验证集误差的连接权和阈值

 

正则化（regularization）

在误差目标函数中加入一个用于描述网络复杂度的部分，例如加入连接权的平方和，可以使得连接权不会过大，从而使网络输出更光滑，避免过拟合。

 

---

全局最小（global minimum）与局部极小（local minimum）

参数空间中梯度为零的点，只要误差值小于邻近点误差值（这个邻近是全部，不是任一），就是局部极小点。

全局最小点则是整个参数空间内误差值最小的点，全剧最小点是唯一的（值唯一而非点唯一），局部极小点可能存在多个。

 

【跳出局部极小的方法】

           1.多个初始参数值

           2.模拟退火（simulated annealing）

                     在每一步以一定概率接受“次优解”，该概率随时间下降，从而保证稳定性

           3.随机梯度下降

                     计算方法与梯度下降法不一致，有机会跳出局部极小点 

 

---

其他常见神经网络

RBF网络（Radial Basis Function）：径向基函数网络

ART网络（competitive learning）：“胜者通吃”网络

SOM网络（Self-Organizing Map）：自组织映射网络

级联相关网络：一种结构自适应网络

Elman网络：一种最常用的 递归神经网络（recurrent neural networks）

Boltzmann机：一种基于“能量”的模型

 

---

深度学习（deep learning）

理论上，隐层越多、神经元越多的复杂模型能够完成更复杂的学习任务。增加隐层比增加单层神经元更加有效率，不过多隐层神经网络训练可能会发散。

无监督逐层神经网络（unsupervised layer-wise training）

每次训练一层隐结点，训练时将上一层隐结点的输出作为下层隐结点的输入，全部完成后再进行微调（fine-tuning）

权共享（weight sharing）

让一组神经元使用相同的连接权。比如CNN（卷积神经网络）就是采用权共享的方式，大量减少了需要训练的参数数目。

值得注意的是，在CNN中，常使用ReLU（Rectified Linear Unit）进行激活。

                                                                         

深度学习主要是对输入信号进行逐层加工，提取高层特征表示，可以理解成进行种“特征学习”（feature learning）或“表示学习”（representation learning）。

 

【神经网络相关推荐】

书：

Haykin，Neural Networks:A Comprehensive Foundation,2nd Edition，1998

C. M. Bishop，Neural Networks for Pattern Recognition. 1995

学术期刊：

Neural Computation

Neural Networks

IEEE Transactions on Neural Networks and Learning Systems

学术会议：

国际神经信息处理系统会议（NIPS）

国际神经网络联合会议（IJCNN）

欧洲神经网络会议（ICANN）

亚太神经网络会议（ICONIP）

 

---