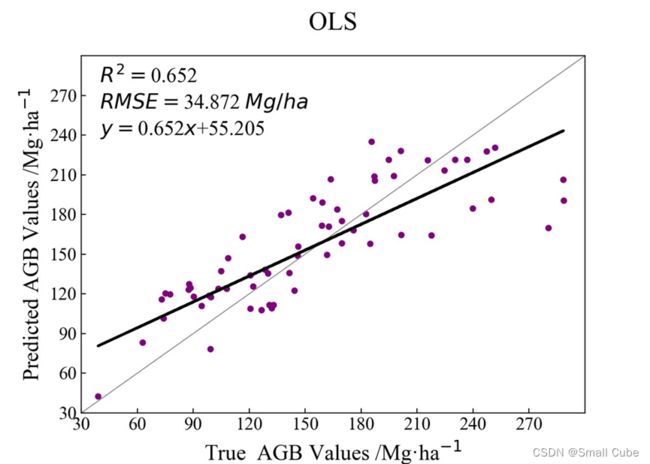
Matlab 多元线性回归

---

前言

使用matlab对tif格式的遥感影像进行多元线性回归，建立用NDVI、EVI、VV、VH等数据反演地上森林生物量（AGB）的方程。

一、原理

---

$$Y=a_0+a_1\ast X_1+a_2\ast X_2+\cdot \cdot \cdot +a_n\ast X_n$$

其中$Y$是AGB，自变量$X_i$分别为Red、NDVI、VV等值。现需要通过已知的同名点$（X_i,Y）$建立方程求解各自变量系数$a_i$，然后将Red、NDVI、VV等影像带入公式中，求解出Y的值（即待反演的AGB影像）。

二、预处理

2.1 变量筛选

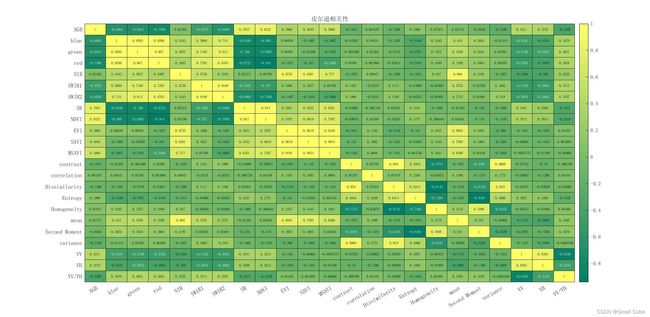
共有blue、green、red、NIR、SWIR1、SWIR2、SR、NDVI、EVI、SAVI、MSAVI、contrast、correlation、Dissimilarity、 Entropy、Homogeneity、mean、Second Moment、variance、VV、VH、VV/VH22个自变量和AGB用来回归，首先进行变量的筛选

%A=xlsread('D:\shixi\model\data.xlsx');
%Y=A(:,1);
%for i=1:23
 %   X(i)=A(:,i);
%end
%X1=A(:,2);

%data3=xlsread('D:\shixi\model\data.xlsx');

%figure
% 求维度之间的相关系数
%rho = corr(data3, 'type','pearson');
% 绘制热图
%string_name={'AGB','blue','green','red','NIR','SWIR1','SWIR2','SR','NDVI','EVI','SAVI','MSAVI','contrast','correlation','Dissimilarity','Entropy','Homogeneity','mean','Second Moment','variance','VV','VH','VV/VH'};
%xvalues = string_name;
%yvalues = string_name;
%h = heatmap(xvalues,yvalues, rho, 'FontSize',10,'FontName','宋体');
%h.Title = '皮尔逊相关性';
%colormap summer

结果：从图中可以看出来变量的相关性有大有小，为方便，我们简单筛选出绝对值>0.5的变量用于后续的建模。

2.2 制作训练集和测试集

现在需要把用于回归建模的同名点$（X_i,Y）$按照2：1分成训练集和测试集。
注：此处用的python，测试集：X_test y_test，训练集： x_train y_train

from sklearn.model_selection import train_test_split
import pandas as pd 
import pandas as pd
import numpy as np
from sklearn.model_selection import GridSearchCV  
import matplotlib.pyplot as plt  
from sklearn.metrics import r2_score
from sklearn import neighbors

feature=pd.read_excel("D:\\shixi\\model\\feature.xlsx",header=0)
target=pd.read_excel("D:\\shixi\\model\\target.xlsx",header=0)
# #target = target.values.ravel()

# #############################################################################
#  数据分割，随机化分割，测试集33%
x_train, x_test, y_train, y_test = train_test_split(feature, target, random_state=46, test_size=0.33)
print(x_test.shape)  # 输出测试集的大小

# #存储数据
writer = pd.ExcelWriter("D:\\shixi\\model\\data_SAR+GUANG.xlsx")      # 写入Excel文件  
y_train= pd.DataFrame(y_train)  
y_test=pd.DataFrame(y_test)
x_train= pd.DataFrame(x_train)  
x_test=pd.DataFrame(x_test)

#y_forecast.to_excel(writer,sheet_name='forecast',na_rep='nana',index=False)        # ‘page_1’是写入excel的sheet名  
y_test.to_excel(writer,sheet_name='y_test',na_rep='nana',index=False)
x_test.to_excel(writer,sheet_name='x_test',na_rep='nana',index=False)
x_train.to_excel(writer,sheet_name='x_train',na_rep='nana',index=False)
y_train.to_excel(writer,sheet_name='y_train',na_rep='nana',index=False)
writer.save()  

三、实现过程

3.1 回归拟合(建模)

代码如下（示例）：

data=xlsread('D:\shixi\model\x_train.xlsx');
Y=xlsread('D:\shixi\model\y_train.xlsx');

X1=data(:,1);
X2=data(:,2);
X3=data(:,3);
X4=data(:,4);
X5=data(:,5);
X6=data(:,6);
X7=data(:,7);
X8=data(:,8);
X9=data(:,9);
X10=data(:,10);

X_part = [ones(size(X1)) X1 X2  X3 X4 X5 X6 X7 X8 X9 X10];
[b_part,bint_part,r_part,rint_part,stats_part] = regress(Y,X_part);

b_part中存放的即为自变量的系数$a_i$，至此我们得到了建立的模型
$Y_{pre}=73.2581830366806-5217.90689393932\ast X1-2392.40872194445\ast X2+4763.08909146459\ast X3-65.0148457996989\ast X4+7.58869625169745\ast X5-55.9981404371055\ast X6+1625.08894546664\ast X7-1283.26083235081\ast X8+12.4042711909978\ast X9+108.253740289186\ast X10;$

3.2 测试

data2=xlsread('D:\shixi\model\x_test.xlsx');
Y_test=xlsread('D:\shixi\model\y_test.xlsx');
T1=data2(:,1);
T2=data2(:,2);
T3=data2(:,3);
T4=data2(:,4);
T5=data2(:,5);
T6=data2(:,6);
T7=data2(:,7);
T8=data2(:,8);
T9=data2(:,9);
T10=data2(:,10);

Y_pre=73.2581830366806-5217.90689393932*T1-2392.40872194445*T2 +4763.08909146459*T3-65.0148457996989*T4 +7.58869625169745*T5 -55.9981404371055*T6 +1625.08894546664*T7-1283.26083235081* T8 +12.4042711909978*T9 +108.253740289186*T10;
Y_pre_part = [ones(size(Y_pre)) Y_pre];
[b_pre_part,bint_pre_part,r_pre_part,rint_pre_part,stats_pre_part] = regress(Y_test,Y_pre_part);

精度如下：

3.3 预测

读取NDVI等影像，用于预测AGB。
代码如下（示例）：

[a,R]=geotiffread('D:\shixi\AGB\8.tif');%先导入某个图像的投影信息，为后续图像输出做准确
info=geotiffinfo('D:\shixi\AGB\8.tif')
k=1;
for num=1:8
     file=['D:\shixi\AGB\',int2str(num),'.tif'];
    bz=importdata(file);
    [c,o]=size(bz);
    bz=reshape(bz,c*o,1);
    data(:,k)=bz;
    k=k+1;
end
T1=data(:,1);
T2=data(:,2);
T3=data(:,3);
T4=data(:,4);
T5=data(:,5);
T6=data(:,6);
T7=data(:,7);
T8=data(:,8);
T9=data(:,9);
T10=data(:,10);
Y_pre=73.2581830366806-5217.90689393932*T1-2392.40872194445*T2 +4763.08909146459*T3-65.0148457996989*T4 +7.58869625169745*T5 -55.9981404371055*T6 +1625.08894546664*T7-1283.26083235081* T8 +12.4042711909978*T9 +108.253740289186*T10;

AGB= reshape(data, c,o);
name2='D:\shixi\AGB\predict.tif';
geotiffwrite(name2,AGB,R,'GeoKeyDirectoryTag',info.GeoTIFFTags.GeoKeyDirectoryTag);

结果：

---

总结

总的过程大致可以分为：数据预处理、建模（多元线性）、测试、预测这四个步骤。如需后续建不同的模型，只需把建模的过程换成其他的模型（如RF\KNN\SVR等机器学习或深度学习）即可。
注：①、个人认为现阶段遥感参数反演大部分进入了半经验半理论模型时期（至少我从课堂和参加一些会议时看到的情况是这样的），也就是说从理论层面提取出来我们所需要的自变量，然后用经验公式来建模这个方法几乎用在了参数反演的方方面面。所以我们学会这一个最简单的方法后举一反三再去做其他模型大同小异。
②、至于影响精度的因素就是各方面的了，“数据质量决定了模型精度的极限，而你选用的模型和参数只能无限逼近这个极限”。前期数据的选取和数据的预处理还是极其重要的，毕竟巧妇难为无米之炊。