Chapter 4 朴素贝叶斯算法与手写数字识别实战

1. 理论推导

1．朴素贝叶斯法是典型的生成学习方法。生成方法由训练数据学习联合概率分布$P(X,Y)$，然后求得后验概率分布$P(Y|X)$。具体来说，利用训练数据学习$P(X|Y)$和$P(Y)$的估计，得到联合概率分布：
$$P(X,Y)＝P(Y)P(X|Y)$$
概率估计方法可以是极大似然估计或贝叶斯估计。

2．朴素贝叶斯法的基本假设是条件独立性，
$$\begin{array}{rl}P(X& =x|Y=c_k)=P\left(X^{(1)}=x^{(1)},\cdots ,X^{(n)}=x^{(n)}|Y=c_k\right)\\ & =\prod _{j=1}^{n}P\left(X^{(j)}=x^{(j)}|Y=c_k\right)\end{array}$$

这是一个较强的假设。由于这一假设，模型包含的条件概率的数量大为减少，朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效，且易于实现。其缺点是分类的性能不一定很高。

3．朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测。
$$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(Y)P(X|Y)}{{\sum }_{Y}P(Y)P(X|Y)}$$
将输入$x$分到后验概率最大的类$y$。
$$y=\arg \underset{c_k}{\max }P\left(Y=c_k\right)\prod _{j=1}^{n}P\left(X_j=x^{(j)}|Y=c_k\right)$$
后验概率最大等价于0-1损失函数时的期望风险最小化。

补充：

(1) 生成模型和判别模型

**生成方法：**由数据学习联合概率分布$P(X,Y)$,然后求出条件概率分布作为预测的模型，即生成模型：
$$P(Y|X)=\frac{P(X,Y)}{P(X)}$$
这样的方法之所以成为生成方法，是因为模型表示了给定输入$X$产生输出$Y$的生成关系。

**判别方法：**由数据直接学习决策函数$f(x)$或者条件概率分布$P(Y|X)$作为预测的模型，即判别模型，判别方法关心的是对给定的输入$X$,应该预测什么样的$Y$。

2. 常见模型

2.1　多项式模型

​ 在贝叶斯法中，学习意味着估计$P\left(y_k\right)$和条件概率$P\left(x_i|y_k\right)$，而在实际的处理过程中会进行一些平滑处理，保证在某些一般情况下不会存在“０”操作具体公式如下：
$$P\left(y_k\right)=\frac{N_{y_k+\alpha }}{N+k\alpha }$$

$$P\left(x_i|y_k\right)=\frac{N_{y_k,x_i}+\alpha }{N_{y_k}+n\alpha }$$

​ 当$ α=1 $$时，称作Laplace平滑，当$ $0<\alpha <1$时，称作Lidstone平滑，$\alpha =0$时不做平滑。如果不做平滑，当某一维特征的值xixi没在训练样本中出现过时，会导致$P(xi|yk)=0P(xi|yk)=0$，从而导致后验概率为0。加上平滑就可以克服这个问题。

具体实例见书例4.1

2.2 高斯模型

​ 当特征是连续变量的时候，运用多项式模型就会导致很多$P(xi|yk)=0$（不做平滑的情况下），此时即使做平滑，所得到的条件概率也难以描述真实情况。所以处理连续的特征变量，应该采用高斯模型。

特征的可能性被假设为高斯

概率密度函数：
$$P(x_i|y_k)=\frac{1}{\sqrt{2\pi {\sigma }_{yk}^2}}exp(-\frac{(x_i-{\mu }_{yk}{)}^2}{2{\sigma }_{yk}^2})$$
数学期望(mean)：$\mu$

方差：${\sigma }^2=\frac{\sum (X-\mu {)}^2}{N}$

代码实现：

# 1.数据预处理
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

from collections import Counter
import math

# data
def creat_data():
    iris = load_iris()
    df = pd.DataFrame(iris.data, columns=iris.feature_names)
    df["label"] = iris.target
    df.columns = ["sepal length", "sepal width", "petal length","petal width", "label"]
    print(df.shape)
    data = np.array(df.iloc[:100, :])#加载数据集前100个　标签为0,1
    #print(data)
    return data[:, :-1], data[:, -1]

X, y = creat_data()
#随机分离数据集函数
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

#2.贝叶斯法
class NaiveBayes:
    
    def __init__(self):
        self.model = None
        
    #数学期望
    @staticmethod
    def mean(X):
        return sum(X)/float(len(X))
    
    #标准差
    def stdev(self, X):
        avg = self.mean(X)
        return math.sqrt(sum([pow(x-avg, 2) for x in X])/float(len(X)))
        
    #概率密度函数
    def gaussian_probability(self, x, mean, stdev):
        exponent = math.exp(-(math.pow(x- mean, 2)/(2*math.pow(stdev, 2))))
        
        return 1 / math.sqrt(2*math.pi*math.pow(stdev, 2))*exponent
    
    #处理X_train数据,得到列向量的均值和方差
    def summarize(self, train_data):
        #print(train_data)
#         for i in zip(*train_data):
#             print(i)
        summaries = [(self.mean(i), self.stdev(i)) for i in zip(*train_data)]#取出每一个数行的z
        #print(summaries)
        return summaries
    
    #分别求出期望和方差
    def fit(self, X, y):
        labels = list(set(y))#set()构建一个不重复的集合
        print("labels:",labels)
        #封装数据为为字典
        data = {label : [] for label in labels}
        for f, label in zip(X, y): 
            data[label].append(f)#添加数据字典
            
        self.model = {
            label: self.summarize(value) for label, value in data.items()
        }
        print("model:", self.model)
        return 'gaussian NB train done!'
    
    #计算概率
    def calculate_probabilities(self, input_data):
        probabilities = {}
        for label,value in self.model.items():
            probabilities[label]=1#保证非零
            print("value:", value)
            for i in range(len(value)):
                #print(i," : ",value[i])
                mean, stdev = value[i]
                probabilities[label] *= self.gaussian_probability(
                input_data[i], mean, stdev)
          
        print("可能:",probabilities)
        return probabilities

    # 类别
    def predict(self, X_test):
        # {0.0: 2.9680340789325763e-27, 1.0: 3.5749783019849535e-26}
        label = sorted(
            self.calculate_probabilities(X_test).items(),
            key=lambda x: x[-1])[-1][0]
        return label

    def score(self, X_test, y_test):
        right = 0
        for X, y in zip(X_test, y_test):
          
            label = self.predict(X)  
            print("label:",label)
            print("True:", y)
            if label == y:
                right += 1


                return right / float(len(X_test))
if __name__ == "__main__":
    model = NaiveBayes()
	model.fit(X_train, y_train)
	print(model.predict([4.4,  3.2,  1.3,  0.2]))
	model.score(X_test, y_test)

3 手写数字识别实战

import pandas as pd
import numpy as np
import matplotlib.pylab as plt
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
import math
from sklearn.metrics import confusion_matrix
import seaborn as sns

3.1 加载数据

digits = load_digits()

X = digits.data
Y = digits.target

3.2 ⼆值化（离散化

df = pd.DataFrame(X)

for i in range(len(df)):
    ave = df.iloc[i, :].sum()/64
    temp1 = df.iloc[i, :]>=ave
    temp2 = df.iloc[i, :]<ave
    df.loc[i, temp1] = 1
    df.loc[i, temp2] = 0

df.iloc[0, :].hist()
plt.show()

# 转为ndarry类型数据
X = df.values
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X, Y
, test_size = 0.3
, random_state =0
)

3.3 可视化化数据

fig, ax = plt.subplots(4, 5
                    , figsize= (10,8)
                    , subplot_kw = {"xticks":[], "yticks":[]}
                    )

for i ,ax in enumerate(ax.flat):
    ax.imshow(Xtrain[i, :].reshape(8, 8)
            ,cmap="gray"
            )
plt.show()

3.4 ⻉叶斯算法

class NaivaBayes:
    """最⼩⻛险朴素⻉叶斯"""
    def __init__(self, alpha=1, fit_prior=True, class_prior=None):
        self.alpha = alpha
        self.fit_prior = fit_prior
        self.class_prior = class_prior # 先验
        self.classes = None # 类别
        self.conditional_prob = None # 类条件概率（特征独⽴性假设）
        
    def calculate_feature_prob(self, feature):
        values = np.unique(feature) # 特征的可能取值
        total_num = float(len(feature))
        value_prob = {}
        for v in values:
            value_prob[v] = ((np.sum(np.equal(feature, v))
                                + self.alpha)/(total_num + len(values)*self.alpha))
        # 填充⾮零项
        if 1.0 not in value_prob.keys():
            value_prob[1.0] = 0.0
        if 0 not in value_prob.keys():
            value_prob[0.0] = 0.0
        return value_prob
    
    def fit(self, X, y):
        self.classes = np.unique(y)
        # 计算先验概率
        if self.class_prior == None:
            class_num = len(self.classes)
            if not self.fit_prior: # 如果不设置先验，则将先验概率等分
                self.class_prior = [1.0/class_num for _ in range(class_num)]
            # 统计先验概率
            else:
                self.class_prior = []
                sample_num = float(len(y))
                for c in self.classes:
                    c_num = np.sum(np.equal(c, y))
                    # 加⼊平滑
                    self.class_prior.append((c_num + self.alpha) / (sample_num +
                                            class_num*self.alpha))
        
        # 计算⻉叶斯条件概率
        self.conditional_prob = {}
        # 分别计算每⼀个类别
        for c in self.classes:
            self.conditional_prob[c] = {}
            
            # 计算每⼀个特征
            for i in range(len(X[0])):
                feature = X[np.equal(y, c)][:, i]
            
                # 保存c_j类的f_i类特征
                self.conditional_prob[c][i] = self.calculate_feature_prob(feature)
        return self
    
    def predict_sigle_sample(self, x):
        """最⼩错误的⻉叶斯决策"""
        label = -1
        max_poster_prob = 0
        for c_index in range(len(self.classes)):
            current_class_prior = self.class_prior[c_index] # 取出相应的后验概率
            current_conditional_prob = 1.0 # 当前条件概率
            feature_prob = self.conditional_prob[self.classes[c_index]] #当前类别下的特征概率
            j = 0
            for feature_i in range(len(feature_prob)):
                # 当前类别下的所有的条件概率
                current_conditional_prob *= feature_prob[feature_i][x[j]]
                j += 1
            if current_conditional_prob*current_class_prior>max_poster_prob:
                max_poster_prob = current_class_prior*current_conditional_prob
                label = self.classes[c_index]
        return label
    
    def predict_sigle_expensive(self, x):
        """最⼩⻛险的⻉叶斯决策"""
        label = -1
#         max_poster_prob = 0
        
        current_loss = np.ones((1, len(self.classes)))
        # 使⽤随机的决策⽅程（0， 1）
        decsion_function = np.random.random((len(self.classes), len(self.classes)))
        # decsion_function = np.random.random_integers(10, size=(len(self.classes),
        # len(self.classes)))
        
        for c_index in range(len(self.classes)):
            current_class_prior = self.class_prior[c_index] # 取出相应的后验概率
            current_conditional_prob = 1.0 # 当前条件概率
            feature_prob = self.conditional_prob[self.classes[c_index]] #当前类别下的特征概率
            j = 0
            for feature_i in range(len(feature_prob)):
                # 当前类别下的所有的条件概率
                current_conditional_prob *= feature_prob[feature_i][x[j]]
                j += 1
            current_loss[:, c_index] = current_class_prior*current_conditional_prob
        label = np.argmin(np.matmul(decsion_function, current_loss.T))
        return label
    
    def predict_accuacy(self, Xtest, Ytest, decsion=True):
        if decsion:
            if Xtest.ndim == 1:
                return self.predict_sigle_sample(Xtest)
            else:
                count = 0
                labels = []
                for i in range(Xtest.shape[0]):
                    label = self.predict_sigle_sample(Xtest[i])
                    if label == Ytest[i]:
                        count +=1
                    labels.append(label)
                return count/Xtest.shape[0], np.array(labels)
        else:
            if Xtest.ndim == 1:
                return self.predict_sigle_expensive(Xtest)
            else:
                count = 0
                labels = []
                for i in range(Xtest.shape[0]):
                ##最⼩错误的⻉叶斯
                    label = self.predict_sigle_expensive(Xtest[i])
                    if label == Ytest[i]:
                        count +=1
                    labels.append(label)
                return count/Xtest.shape[0], np.array(labels)

model = NaivaBayes()
model = model.fit(Xtrain,Ytrain)

3.5 最⼩错误的⻉叶斯

# 单个样本的测试
model.predict_sigle_sample(Xtest[0])

2

accuracy, Ypred = model.predict_accuacy(Xtest, Ytest)
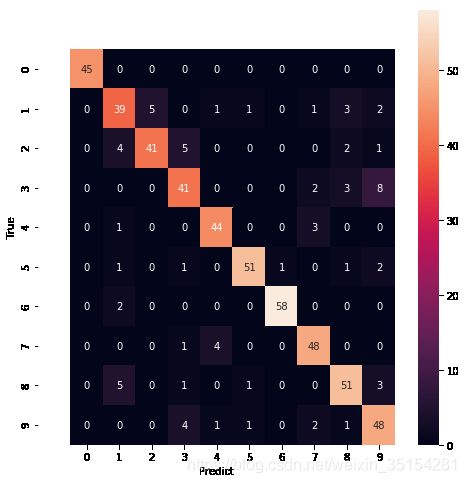
print("Accuracy:%0.3f" % (accuracy))

Accuracy:0.863

cm = confusion_matrix(Ytest, Ypred)
fig, axes = plt.subplots(1, 1, figsize=(8, 8))
sns.heatmap(cm, annot=True, ax = axes)
axes.set_xlabel("Predict")
axes.set_ylabel("True")
axes.set_xlim([-1,10])
axes.set_ylim([10,-1])
plt.show()

fig, ax = plt.subplots(1, 10
                        , figsize= (10,10)
                        , subplot_kw = {"xticks":[], "yticks":[]}
                        , squeeze = False
                        )
for i ,ax in enumerate(ax.flat):
    ax.imshow(Xtest[i, :].reshape(8, 8)
    ,cmap="gray"
    )
    ax.set_title("Ture:{}\nPred:{}".format(Ytest[i], Ypred[i]))
plt.show()

3.6 最⼩⻛险的⻉叶斯

# 单个样本的决策
model.predict_sigle_expensive(Xtest[0])

8

#测试集预测(基于最⼩⻛险的⻉叶斯，取决与不同的决策⾯⽅程，此次决策⾯⽅程随机抽取，所以准确率较低，可
#以进⾏⼈为调节)
accuracy, Ypred = model.predict_accuacy(Xtest, Ytest, decsion=False)
print("Accuracy:%0.3f" % (accuracy))

Accuracy:0.119

# 混淆矩阵
cm = confusion_matrix(Ytest, Ypred)
fig, axes = plt.subplots(1, 1, figsize=(8, 8))
sns.heatmap(cm, annot=True, ax = axes)
axes.set_xlabel("Predict")
axes.set_ylabel("True")
axes.set_xlim([-1,10])
axes.set_ylim([10,-1])
plt.show()

fig, ax = plt.subplots(1, 10
                        , figsize= (10,10)
                        , subplot_kw = {"xticks":[], "yticks":[]}
                        , squeeze = False
                        )
for i ,ax in enumerate(ax.flat):
    ax.imshow(Xtest[i, :].reshape(8, 8)
    ,cmap="gray"
    )
    ax.set_title("Ture:{}\nPred:{}".format(Ytest[i], Ypred[i]))
plt.show()

参考链接

朴素贝叶斯的推导
朴素贝叶斯应用