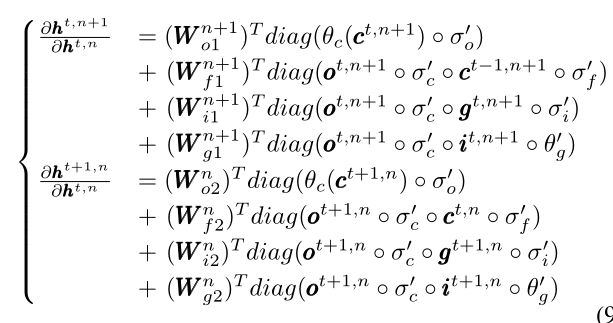文献阅读——Comparing SNNs and RNNs on Neuromorphic Vision Datasets: Similarities and Differences
题目:Comparing SNNs and RNNs on Neuromorphic Vision Datasets: Similarities and Differences
期刊会议:Neural Networks 2020(CCF B)
摘要
记录无框架棘波事件的神经形态数据因其时空信息成分和事件驱动的处理方式而受到广泛关注。脉冲神经网络(SNNs)代表了一族用于神经形态计算的具有时空动力学的事件驱动模型,这些模型在神经形态数据上被广泛基准化。有趣的是,机器学习社区的研究人员可以认为,递归(人工)神经网络(RNNs)也有能力提取时空特征,尽管它们不是事件驱动的。因此,“如果我们在神经形态数据上对这两种模型一起进行基准测试,会发生什么”的问题出现了,但仍然不清楚。
在这项工作中,我们以视觉数据集为例,对SNNs和RNNs在神经形态数据上的比较进行了系统的研究。首先,我们从建模和学习的角度确定了SNNs和RNNs(包括普通RNNs和LSTM)之间的相似性和差异。为了提高可比性和公平性,我们统一了基于时间反向传播(BPTT)的监督学习算法、利用所有时间步长的输出的损失函数、具有堆叠全连接或卷积层的网络结构以及训练期间的超参数。特别地,鉴于RNNs中使用的主流损失函数,我们受码率编码方案的启发对其进行了修改,以接近SNNs的损失函数。此外,我们调整数据集的时间分辨率来测试模型的鲁棒性和泛化能力。最后,在DVS转换(N-MNIST)和DVS捕获(DVS手势)两种神经形态数据集上进行了一系列对比实验。提供了关于识别准确性、特征提取、时间分辨率和对比度、学习泛化、计算复杂性和参数体积的广泛见解,这有利于不同工作负载上的模型选择,甚至有利于未来新神经模型的发明。
1 介绍
神经形态视觉数据集[1]-[3]使用动态视觉传感器(DVS)[4]-[7]感知像素强度的动态变化,并记录由此产生的尖峰事件。与传统的基于帧的视觉数据集相比,无帧神经形态视觉数据集通过交互空间和时间信息具有丰富的时空成分,并遵循由二进制尖峰触发的事件驱动处理方式。由于这些独特的特征,神经形态数据在许多应用中引起了相当大的关注,例如视觉识别[8]-[11][12]-[14],运动分割[15],跟踪控制[16]-[18],机器人学[19]等。目前,有两种类型的神经形态视觉数据集:一种是通过在DVS相机前扫描每个图像从静态数据集转换而来,例如N-MNIST [1]和cifar 10-DVS[3];另一种是由DVS相机从运动物体中直接捕获的,例如DVS手势[14]。
https://zhuanlan.zhihu.com/p/563572382 DVS一些基本原理
受大脑回路启发的脉冲神经网络(SNNs) [20]代表了一系列用于神经形态计算的模型。SNN模型中的每个神经元都会根据记忆的状态和电流输入来更新膜电位,并在膜电位超过某个阈值时触发一个尖峰信号。在人工神经网络(ann)中,脉冲神经元使用二元脉冲事件而不是连续激活来相互通信,SNN模型携带空间和时间信息。SNNs丰富的时空动力学和事件驱动范式在有效处理复杂任务方面具有巨大的潜力,如棘波模式识别[8]、[21]、光流估计[22]以及同时定位和地图(SLAM)构建[23],这促使它们广泛部署在低功率神经形态设备上[24]-[26]。由于snn的行为自然与神经形态数据的特征相匹配,因此大量文献对snn在神经形态数据集上的性能进行了基准测试[12]、[27]-[29]。
最初,神经形态计算和机器学习是并行发展的两个领域,并且通常彼此独立。随着更多跨学科研究的出现,这种情况似乎正在改变[26]、[29]、[30]。在这种情况下,机器学习社区的研究人员可以认为,snn不是处理神经形态数据的唯一方法。原因是递归(人工)神经网络(RNNs)也可以记住以前的状态,并表现出时空动态,即使它们不是事件驱动的。通过将尖峰事件视为{0,1}中的正常二进制值,rnn也能够处理神经形态数据集。本质上,RNNs已经广泛应用于许多具有时序的任务中,例如语言建模[31]、语音识别[32]和机器翻译[33]; 然而,很少有研究评估RNNs在神经形态数据上的性能, 因此提到的争论仍然是开放的。
在这项工作中,我们试图回答当在神经形态数据上对snn和rnn一起进行基准测试时会发生什么,以视觉数据集作为案例研究。首先,我们从建模和学习的角度识别SNNs和RNNs之间的相似性和差异。为了可比性和公平性,我们统一了几个东西:I)基于时间反向传播的监督学习算法(BPTT);ii)受面向SNN的速率编码方案启发的损失函数;iii)基于堆叠全连接(FC)或卷积(Conv)层的网络结构;iv)训练期间的超参数。此外,我们调整神经形态视觉数据集的时间分辨率,以测试模型的鲁棒性和泛化能力。最后,我们在典型的神经形态视觉数据集上进行了一系列对比实验,并提供了广泛的见解。我们的工作有可能指导不同工作负载的模型选择,并刺激新的神经模型的发明。 为了清楚起见,我们总结了我们的贡献如下:
-
我们提出了第一个系统地比较神经形态数据集上的snn和rnn的工作。
-
我们确定了SNNs和RNNs之间的异同,并统一了学习算法、损失函数、网络结构和训练超参数,以确保可比性和公平性。
-
特别地,我们修改了RNNs的主流损失函数以接近SNNs的损失函数,并调整了神经形态视觉数据集的时间分辨率以测试模型的鲁棒性和泛化能力。
-
在两种典型的神经形态视觉数据集上:DVS转换的(N-MNIST)和DVS捕获的(DVS手势),我们进行了一系列对比实验,产生了关于识别准确性、特征提取、时间分辨率和对比度、学习泛化、计算复杂性和参数量的广泛见解(第四节详细介绍,第五节总结),这对未来的模型选择和构建是有益的。
本文的其余部分组织如下:第二节介绍了神经形态视觉数据集,SNNs和RNNs的一些预备知识;第三节详细介绍了我们的方法,使SNNs和RNNs具有可比性,并确保公平性;第四节展示了实验结果并提供了我们的见解;最后,第五部分对论文进行了总结和讨论。
2、预备工作
A、 神经形态视觉数据集
神经形态视觉数据集由许多尖峰事件组成,这些尖峰事件由DVS相机感测场中每个像素的强度变化(增加或减少)触发[4],[5],[18]。DVS摄像机根据不同的变化方向在两个通道中记录尖峰事件,例如,用于强度增加的开启通道和用于强度降低的关闭通道。神经形态视觉数据集中的整个尖峰序列可以表示为H×W×2×T0大小的尖峰模式,其中H、W分别是传感场的高度和宽度,T0代表记录时间的长度,“2”表示两个通道。如引言所述,目前有两种类型的神经形态视觉数据集:转换的DVS和捕获的DVS,详情如下
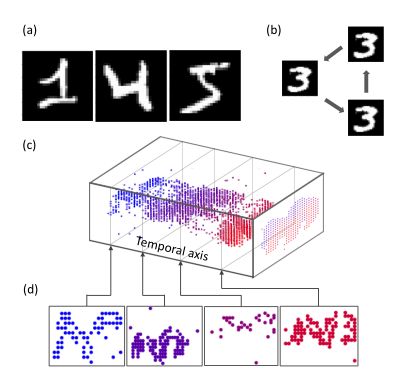
图1:名为NMNIST的DVS转换数据集示例:(a)MNIST数据集中的原始静态图像;(b) 静态图像的重复闭环平滑(RCLS)运动;(c) DVS记录的所得尖峰模式;(d) 不同时间步的尖峰事件切片。蓝色和红色分别表示打开和关闭通道。
DVS捕获的数据集。相反,DVS捕获的数据集通过自然运动而不是DVS转换数据集生成中使用的模拟运动生成尖峰事件。图2描述了名为DVS手势的DVS捕获数据集[14]。每个轨迹中有11个手和手臂姿势由一个受试者执行,在3个数据集中总共有122个轨迹。选择三种照明条件,包括自然光、荧光和LED光,以控制DVS相机上阴影和闪烁的影响,从而改善数据分布的偏差。与DVS转换的数据集不同,DVS捕获的数据集中的时间和空间信息都是必不可少的组成部分。
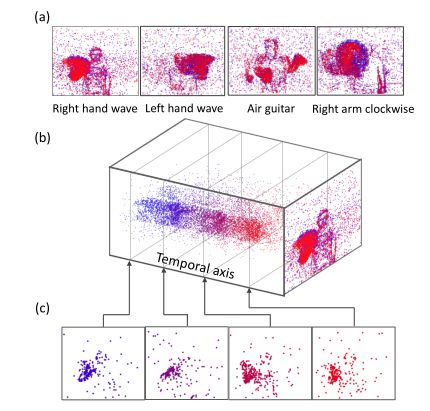
图2:名为DVS手势的DVS捕获数据集示例:(a)尖峰模式示例,其中时间窗口tw内的所有尖峰事件被压缩为单个静态图像以进行可视化;(b) DVS记录的尖峰模式;(c) 在不同时间步长的尖峰事件切片,其中右手位于每个切片中的不同位置,从而沿时间维度形成手波。蓝色和红色分别表示打开和关闭通道。
B、 尖峰神经网络
有几种不同的尖峰神经元模型,如漏积分和激发(LIF)[36]、Izhikevich[37]和Hodgkin Huxley[38],其中LIF因其较低的复杂性而在实践中应用最广泛[39]。在这项工作中,我们采用了主流的解决方案,即采用LIF进行神经元模拟。通过突触连接许多尖峰神经元,我们可以构建SNN模型。在本文中,为了简单起见,我们只考虑具有堆叠FC或Conv层的前馈SNN。
LIF神经元有两个状态变量:膜电位(u)和输出活性(o)。u是连续值,而o只能是二进制值,即是否触发尖峰。SNN层的行为可以描述为
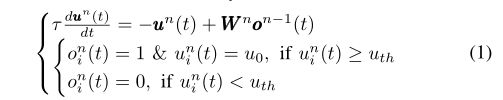
其中t表示时间, n n n和 i i i分别是层和神经元的指数, τ τ τ是时间常数,W是两个相邻层之间的突触权重矩阵。只有当u超过触发阈值( u t h u_{th} uth)时,神经元才会触发尖峰并重置 u = u 0 u=u_0 u=u0,否则,膜电位就会泄漏。注意, o 0 ( t ) o^0(t) o0(t)表示网络输入。
C、循环神经网络
在本研究中,RNN主要指的是循环ANN而不是SNN。本文选择了两种RNN模型:一种是Vanilla RNN,另一种是现代的长短期记忆RNN (LSTM)。
Vanilla RNN。rnn通过循环连接引入时间动力学。在普通RNN神经元中只有一个连续的状态变量,称为隐藏状态(h)。普通RNN层的行为如下:

其中t和n分别为时间步长指标和层数指标, W 1 W_1 W1为相邻两层之间的权矩阵, W 2 W_2 W2为层内循环权矩阵,b为偏置向量。 θ ( ⋅ ) θ(·) θ(⋅)是一个激活函数,对于一般的Vanilla Rnn,它可以是 t a n h ( ⋅ ) tanh(·) tanh(⋅)函数。与SNN的 o 0 ( t ) o^0(t) o0(t)类似, h t , 0 h^{t,0} ht,0也表示RNN的网络输入,即 x t x^t xt
Long Short-Term Memory (LSTM)。LSTM通过引入复门来缓解梯度消失[40],[41],改善了Vanilla RNN的长期时间依赖性。LSTM层可以描述为
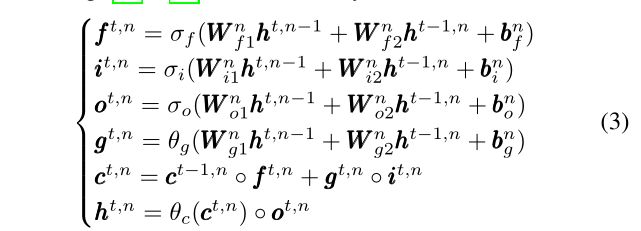 其中t和n分别为时间步和层的指标, f , i , o f,i,o f,i,o分别为遗忘门、输入门和输出门的状态, g g g为输入激活。每个门都有自己的权值矩阵和偏置向量。 c c c和 h h h分别是细胞态和隐态。 σ ( ⋅ ) σ(·) σ(⋅)和 θ ( ⋅ ) θ(·) θ(⋅)分别是sigmoid函数和tanh函数, ◦ ◦ ◦是Hadamard乘积。
其中t和n分别为时间步和层的指标, f , i , o f,i,o f,i,o分别为遗忘门、输入门和输出门的状态, g g g为输入激活。每个门都有自己的权值矩阵和偏置向量。 c c c和 h h h分别是细胞态和隐态。 σ ( ⋅ ) σ(·) σ(⋅)和 θ ( ⋅ ) θ(·) θ(⋅)分别是sigmoid函数和tanh函数, ◦ ◦ ◦是Hadamard乘积。
2 方法
为了避免歧义,我们想再次强调,我们在这项工作中的“SNN vs. RNN”被定义为“feedforward SNNs vs. recurrent ANNs”。为了简单起见,我们只从RNN家族中选择了两个代表,即vanilla RNN和LSTM。在本节中,我们首先从建模和学习的角度重新思考了snn和rnn的异同,并讨论了如何保证可比性和公平性。
A.重新思考相似之处
在分析之前,我们首先将式(1)转换为迭代版本,使其与式(2)(3)的格式兼容。这可以通过求解式(1)中的一阶微分方程来实现,得到
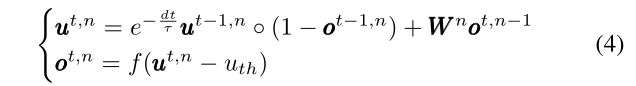
其中 e − d t τ e^{-\frac{dt}{\tau }} e−τdt反映膜势的泄漏效应,f(·)是一个阶跃函数,满足f(x) = 1当x≥0时,否则f(x) = 0。这个迭代LIF模型包含了峰值神经元的所有行为,包括集成、触发和重置。
现在,由式(2)-(4)可以看出,snn和rnn的模型非常相似,包括时间维度和空间维度。图3进一步可视化了snn、vanilla rnn和LSTM在正向和向后传递中的信息传播路径。这里我们将vanilla RNNs中θ之前的隐藏状态表示为 h ~ \tilde{h} h~ ,将LSTM中 σ 、 θ σ、θ σ、θ之前的门状态表示为 f ~ \tilde{f} f~, i ~ \tilde{i} i~, o ~ \tilde{o} o~, g ~ \tilde{g} g~。
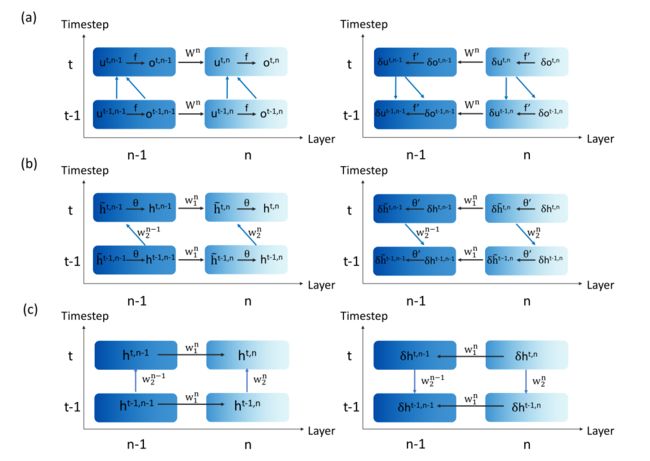
图3:(a) snn、(b) vanilla rnn和 ( c ) LSTM在正向和反向通道中的信息传播路径。为了清晰起见,我们没有展示LSTM神经元内部的数据流。
前进通道的时空动力学。 首先,如果将SNN的u和o分别视为vanilla RNNs的 h ~ \tilde{h} h~和h,那么SNN和vanilla RNNs的正向传播路径是相似的。第二,对于LSTM,神经元内部有更多的中间状态,包括: f ~ \tilde{f} f~, i ~ \tilde{i} i~, o ~ \tilde{o} o~, g ~ \tilde{g} g~和细胞状态。虽然神经元变得复杂,但如果只关注隐藏状态h的传播,整体时空路径还是相似的。有趣的是,每一个尖峰神经元的内膜电位可以直接影响下一个时间步的神经元状态,这与普通的rnn不同,但类似于LSTM的遗忘门。
时空的反向传播。 对于snn,文献中的学习算法差异显著,如无监督学习[42]、ANN-to-SNN转换[43]、监督学习[12]、[21]、[44]。
由于在机器学习领域,RNN通常由基于梯度下降的监督算法训练,我们选择了最近BPTT-启发的时空反向传播算法[12],[21]用于SNN,以使我们的比较公平。
同样从图3可以看出,SNN、vanilla RNN和LSTM的梯度传播路径也遵循类似的时空规律。此外,我们详细说明了每个模型的反向传播公式,以便更好地理解。注意变量δ表示梯度,例如, ∂ o = ∂ L ∂ o , L ∂o =\frac{∂L}{∂o},L ∂o=∂o∂L,L是网络的损失函数。
对于SNN,我们有
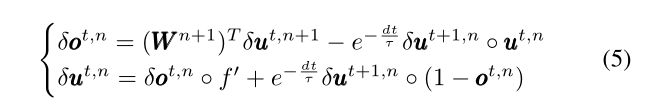
发射函数是不可微的。为此,引入一个类狄拉克函数来逼近其导数[12]。具体来说,f0(·)可以用
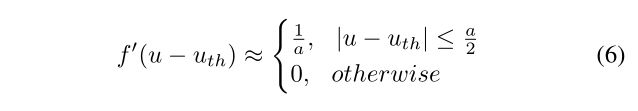
其中a是一个超参数,用于在反向传播期间通过发射函数时控制梯度宽度。对于普通rnn,我们有一个类似的格式如下

对于LSTM,由于门之间的相互作用,情况变得复杂。具体来说,我们可以有类似的
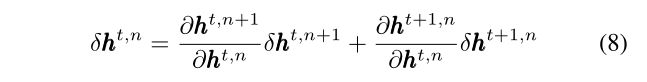 其中右侧的两项分别表示空间梯度反向传播和时间梯度反向传播。此外,我们可以让
其中右侧的两项分别表示空间梯度反向传播和时间梯度反向传播。此外,我们可以让
B.重新思考差异
尽管snn、vanilla rnn和LSTM在信息传播路径上是相似的,但它们仍然有很大的不同。在本小节中,我们将对它们的差异进行思考。
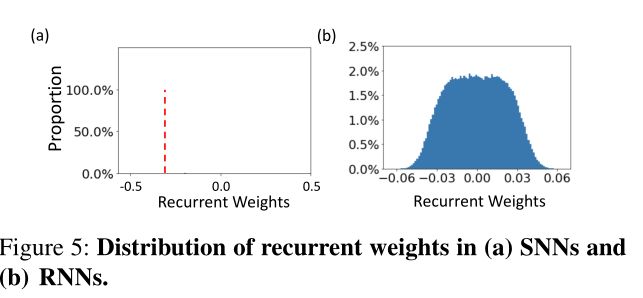
连接模式。 由式(2)-(4)可以看出,这些模型的连接方式是不同的。首先,对于同一层的神经元,snn只在每个神经元内部进行自我递归,而rnn在神经元之间进行交叉递归。具体来说,自我递归意味着只有神经元内部的递归连接;相比之下,交叉递归允许每层神经元之间的递归连接。其次,snn的递归权值由膜电位的泄漏因子决定,其受限于 − e − d t τ -e^{-\frac{dt}{\tau }} −e−τdt ;而在rnn中,循环权值是可训练的参数。为了说明这一点,我们用图4可视化了snn和rnn的连接模式,用图5展示了从实际模型中收集到的循环权的分布,反映了理论分析的结果。

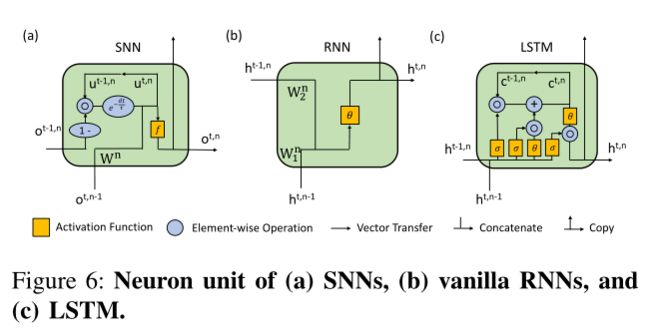
神经元模型。 除了对连接模式的分析,我们还讨论了每个神经元单元内部的建模细节。如图6所示,显然,与LSTM中的复杂门不同,普通rnn中没有门。对于snn,如前所述,膜外电位路径类似于LSTM的遗忘门;然而,复位机制限制了膜电位,不像LSTM中无边界的细胞状态。此外,如图7所示,snn的激活函数是一个发射函数,它本质上是一个具有二进制输出的阶跃函数;而vanilla RNN和LSTM中的激活函数是tanh和sigmoid等连续函数。
损失函数。 在基于梯度下降的监督学习框架下,损失函数对整体优化至关重要。snn和rnn的损失函数格式不同。具体来说,对于snn,通常将峰率编码方案与均方误差(MSE)结合起来形成损失函数,损失函数可以抽象为
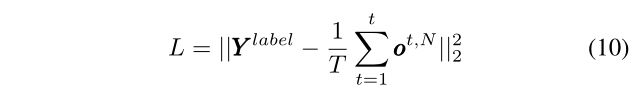
其中 Y l a b e l Y^{label} Ylabel为标签, o t , N o^{t,N} ot,N为最后一层的输出,T为训练过程中的模拟时间步数。该损失函数考虑了在所有时间步长的输出峰值,因此神经元的峰值决定了识别结果。与式(10)不同,rnn的主流损失函数通常服从
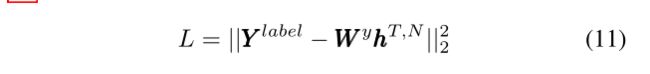 其中 h T , N h^{T,N} hT,N是最后一层在最后一个时间步处的隐藏状态, W y W^y Wy是一个可训练权值矩阵。
其中 h T , N h^{T,N} hT,N是最后一层在最后一个时间步处的隐藏状态, W y W^y Wy是一个可训练权值矩阵。
C.比较方法
基于上述分析,我们在表i中总结了snn、vanilla rnn和LSTM之间的异同。由于它们具有相似的时空动态,因此可以在神经形态数据集上对所有这些模型进行基准测试。此外,面对差异,我们适当统一了以下几个方面,以确保评估的可比性和公平性。

1) 数据集选择和时间分辨率调优:
我们在两个神经形态视觉数据集上对所有模型进行基准测试:一个是名为N-MNIST的DVS转换数据集,另一个是名为DVS Gesture的DVS捕获数据集,这两个数据集已经在第II-A节中介绍过。两个选定数据集的详细信息见表二。对于snn来说,由于具有相同的时空成分和事件驱动方式,神经形态数据的处理是自然的;而对于rnn,峰值数据仅作为二进制值处理,即{0,1}。

通常情况下,每一个尖峰图案的原始记录时间长度都很长,如 1 0 5 10^5 105。其根本原因是由于分布式相机的精细时间分辨率,最初在µs水平。但是神经网络的模拟时间步数不能太大,否则训练时的时间和内存成本是无法承受的。为此,我们考虑了调整时间分辨率的灵活性。具体地说,在每个时间分辨率单元内的原始数据集中,每一个连续的峰值事件片都沿着时间维度折叠成一个片。这里的时间坍缩意味着,如果在坍缩窗口内的任何原始切片的同一位置存在峰值,那么在生成的像素上将出现一个峰值。我们将崩溃过程描述为
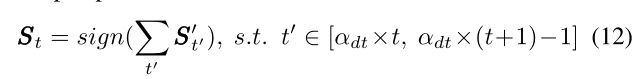 式中, S ′ S' S′为原始切片序列, t ′ t' t′为原始记录时间步指数,S为折叠后的新切片序列,t为新的记录时间步指数, α d t α_{dt} αdt为时间分辨率因子。 s i g n sign sign定义为:符号 s i g n ( x ) = 1 , i f x > 0 ; s i g n ( x ) = 0 , i f x = 0 ; i f x < 0 , 则 s i g n ( x ) < 0 。 sign(x) = 1,i\!f \ x > 0;sign(x)= 0,i\!f \ x = 0;i\!f \ x < 0,则sign(x) < 0。 sign(x)=1,if x>0;sign(x)=0,if x=0;if x<0,则sign(x)<0。折叠后,原切片序列 S t ′ ′ , t 0 ∈ [ 0 , T 0 − 1 ] {S'_{t'}, t_0∈[0,T_0−1]} St′′,t0∈[0,T0−1]成为新的切片序列 S t , t ∈ [ 0 , T 0 / α d t − 1 ] {S_t, t∈[0,T_0 /α_{dt}−1]} St,t∈[0,T0/αdt−1]。
式中, S ′ S' S′为原始切片序列, t ′ t' t′为原始记录时间步指数,S为折叠后的新切片序列,t为新的记录时间步指数, α d t α_{dt} αdt为时间分辨率因子。 s i g n sign sign定义为:符号 s i g n ( x ) = 1 , i f x > 0 ; s i g n ( x ) = 0 , i f x = 0 ; i f x < 0 , 则 s i g n ( x ) < 0 。 sign(x) = 1,i\!f \ x > 0;sign(x)= 0,i\!f \ x = 0;i\!f \ x < 0,则sign(x) < 0。 sign(x)=1,if x>0;sign(x)=0,if x=0;if x<0,则sign(x)<0。折叠后,原切片序列 S t ′ ′ , t 0 ∈ [ 0 , T 0 − 1 ] {S'_{t'}, t_0∈[0,T_0−1]} St′′,t0∈[0,T0−1]成为新的切片序列 S t , t ∈ [ 0 , T 0 / α d t − 1 ] {S_t, t∈[0,T_0 /α_{dt}−1]} St,t∈[0,T0/αdt−1]。
显然,实际的时间分辨率(dt)满足
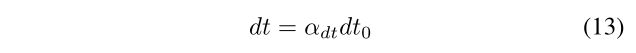 其中 d t 0 dt_0 dt0为原始时间分辨率。图8展示了 α d t α_{dt} αdt = 3的暂时性崩溃的例子。
其中 d t 0 dt_0 dt0为原始时间分辨率。图8展示了 α d t α_{dt} αdt = 3的暂时性崩溃的例子。

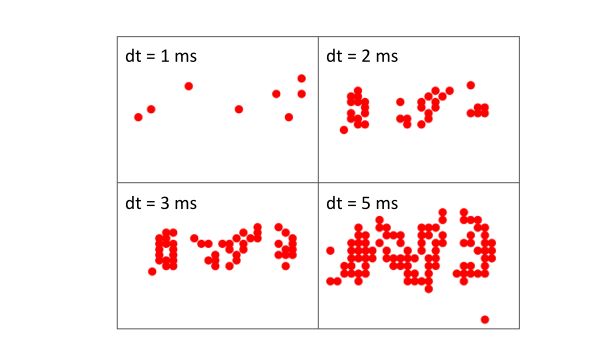
大的时间分辨率将增加新片的峰值率,如图9所示。此外,在式(2)-(4)中的每个模拟时间步中,神经网络在时间崩溃后处理一个切片。因此,在模拟时间步长T固定的情况下,较大的时间分辨率可以延长实际模拟时间,从而能够捕获神经形态数据集中更多的时间依赖性。通过调整时间分辨率,我们创造了从模型性能的变化中提取更多见解的机会。
2) 学习算法与损失函数设计:
由于rnn通常是通过有监督的BPTT算法训练的,为了使比较公平,我们选择了一种最近的BPTT启发的具有时空梯度传播的SNNs[12]学习算法。对于梯度下降所需的损失函数7,基于速率编码方案和MSE的式(10)中损失函数7被广泛应用于snn。
在该损失函数下,每一个时间步都有梯度反馈,可以在一定程度上缓解梯度消失问题。
相比之下,现有的rnn损失函数比较灵活,如式(11)所示的主流损失函数只考虑最后一个时间步的输出,其他损失函数则考虑所有时间步[45]-[47]的输出,如
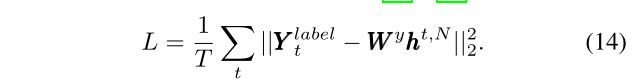
但是,即使使用上述考虑所有时间步下输出的损失函数,对于snn的损失函数仍与式(10)略有不同。为了使比较更加公平,我们为rnn提供了两种损失函数配置。一是主流损失函数如式(11);二是式(14)的修正式,即
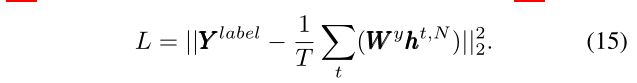
为清晰起见,我们将rnn(15)式中的上述格式称为速率编码启发的损失函数。
3) 网络结构及超参数设置:
基于FC层的结构广泛应用于snn和rnn中,本文将其称为基于多层感知器(MLP)的结构。然而,基于mlp的结构的学习性能通常较差,尤其是在视觉任务中。为此,在snn中引入基于Conv层的结构来提高学习性能[21],本文将其称为基于卷积神经网络(convolutional neural network, CNN)的结构。针对这种情况,除了基本的MLP结构外,我们还实现了rnn的CNN结构,包括vanilla rnn和LSTM。这样就把不同模型之间的比较限制在同一个网络结构上,更加公平。表III提供了不同数据集上的网络结构配置。由于N-MNIST是一个更简单的任务,我们只使用MLP结构;而对于DVS Gesture,我们采用了MLP和CNN两种结构。

除了网络结构外,训练过程还需要一些超参数,如课时数、时间步数、批大小、学习率等。为了保证公平性,我们统一了不同模型的训练超参数。
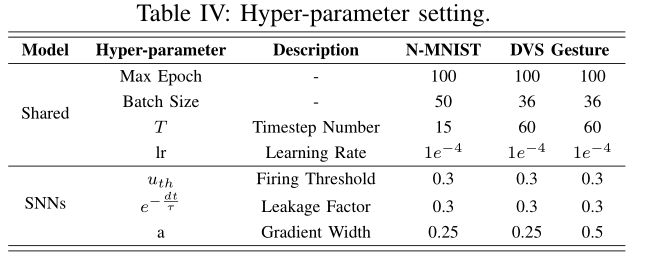
综上所述,通过上述对异同的反思和提出的解决方案,我们成功地统一了测试数据集、时间分辨率、学习算法、损失函数、网络结构、超参数等几个方面,如表V所示。
这种统一既保证了snn和rnn之间的可比性,又使比较更加公平,为本文的研究奠定了基础。

四、结果
通过表V中提到的统一,我们进行了一系列对比实验,并在本节中提取了一些见解。
A.实验设置
所有模型都在开源框架Pytorch[48]中实现。表III和表IV分别给出了网络结构和训练超参数的配置。时间分辨率在N-MNIST上有6个级别 ( d t = 1 m s , 2 m s , 3 m s , 5 m s , 10 m s , 20 m s ) (dt = {1ms, 2ms, 3ms, 5ms, 10ms, 20ms}) (dt=1ms,2ms,3ms,5ms,10ms,20ms),在DVS Gesture上有6个级别 ( d t = 1 m s , 5 m s , 10 m s , 15 m s , 20 m s , 25 m s ) (dt = {1ms, 5ms, 10ms, 15ms, 20ms, 25ms}) (dt=1ms,5ms,10ms,15ms,20ms,25ms)。在给定的模拟时间步数(即T)下,这意味着在训练和测试中只使用每个spike模式的前T个切片。通常,我们固定T值;而在第四-C节中,我们固定模拟时间长度(即T × dt)而不是T。除非另有说明,否则泄漏因子(即 − e − d t τ -e^{-\frac{dt}{\tau }} −e−τdt)固定为0.3。此外,在默认参数设置 ( α = 1 e − 4 , β 1 = 0.9 , β 2 = 0.999 , ϵ = 1 e − 8 ) (α = 1e−4,β1 = 0.9, β2 = 0.999, \epsilon = 1e−8) (α=1e−4,β1=0.9,β2=0.999,ϵ=1e−8)用于网络参数的调整。
B.整体精度比较
表VI-VIII列出了在N-MNIST和DVS手势数据集上进行的一系列对比实验的准确性结果。
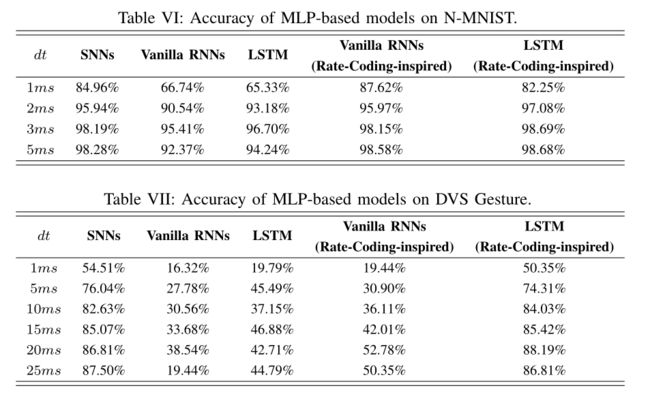
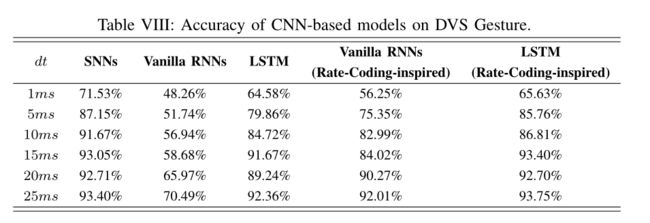
在N-MNIST上,snn在常用模型中达到了最佳的精度。有趣的是,当我们应用速率编码启发的损失函数(式(15))时,rnn可以达到与snn相当甚至更好。在DVS Gesture中也发现了类似的趋势。然而,即使使用了速率编码启发的损失函数,vanilla RNN在DVS手势上的表现似乎也不能超过SNN,特别是在基于MLP的情况下。==潜在的原因可能是由于梯度问题。==众所周知,与vanilla RNNS相比,LSTM可以通过复杂的门结构来缓解梯度消失问题,从而实现更长的时间依赖性[40],[41]。对于SNN而言,膜电位可以直接影响下一个时间步的神经元状态,从而在正向和反向传递过程中,在vanilla rnn上多出一条信息传播路径(见图3)。这条额外路径的作用类似于LSTM的遗忘门(即LSTM[50]最重要的门),因此它也可以比vanilla RNN 记忆更长的依赖性,提高准确性。
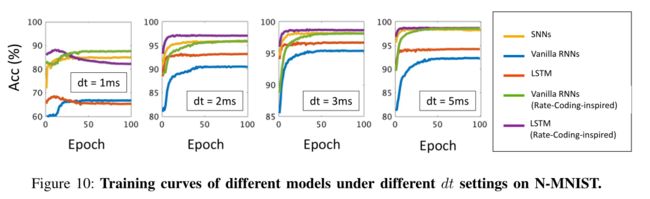
图10进一步给出了这些模型在N-MNIST上的训练曲线。可以观察到,普通的RNN在神经形态数据集上收敛性较差,而具有速率编码启发损失函数的RNN可以向上移动训练曲线,这说明了速率编码启发损失函数的有效性。此外,我们发现SNN和LSTM收敛速度比普通RNN快。所有这些观察结果与表6-8的结果一致。

图11:在DVS Gesture上基于不同cnn的模型中跨时间步的特征映射的可视化。设dt = 15ms,以左臂顺时针方向为例。
除了上述分析之外,我们还进一步在DVS Gesture上可视化Conv层的特征映射,以查看发生了什么,如图11所示。为了简单起见,这里我们只考虑dt = 15ms的情况;采用基于速率编码的损失函数对RNN模型进行了改进。在三种模型中,vanilla RNN具有最清晰的特征映射,接近相应时间步长的输入片。然而,SNN和LSTM模型的特征图显然包含了当前时间步长和之前时间步长的痕迹的整合,这与SNN的额外膜势路径和LSTM复杂的门结构有关。在snn和LSTM的特征图中,动态手势经过的整个区域都被点亮,看起来就像彗星一样。这种特征的整合强化了时间依赖性,在一定程度上改变了后一层从学习时间特征到学习空间特征的过程。在像DVS Gesture这样的DVS捕获数据集上,跨越时间步的不同输入片共同构成了要识别的最终模式;而在dvs转换的数据集如N-MNIST上,不同时间步长的切片是接近的。这一点,加上snn和LSTM的较长记忆,可以解释在DVS Gesture上,vanilla RNN和SNN 、LSTM之间的精度差距比在N-MNIST上更大。
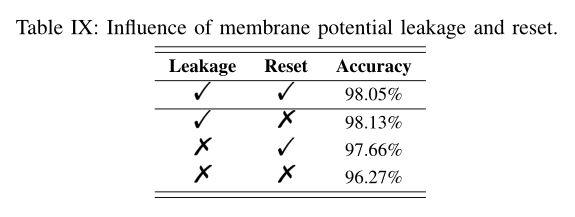
此外,我们还做了一个额外的实验,研究了膜电位泄漏和复位机制对snn的影响。这里我们在N-MNIST上测试dt = 7.5ms。如表九所示,删除这些机构将降低精度。事实上,泄漏和重置都可以降低膜电位,从而在一定程度上降低峰值速率,有助于提高神经元的选择性。有趣的是,我们发现这两种机制的联合影响比其中任何一种的影响都要大。

最后,我们提供了在两个神经形态数据集上应用snn的几个先前工作的准确性结果。请注意,我们没有提供涉及rnn的结果,因为很少有工作在神经形态数据集上测试它们。如表X所示,我们的SNN模型可以达到可接受的结果,尽管不是最好的。由于我们的重点是snn和rnn之间的比较,而不是击败之前的工作,所以我们没有采用之前工作中使用的大型模型和复杂的优化策略来提高准确性。
C.时间分辨率分析
同样从表VI-VIII中,我们发现随着时间分辨率的增大,精度也会提高。原因有两方面:一方面,当dt值较大时,峰值事件变得密集(见图9),这通常在每个切片中形成更多的有效特征;另一方面,在训练过程中模拟时间步数(T)相同的情况下,较大的时间分辨率可以在原始数据集中包含更多的切片,从而提供更多的运动对象信息。 此外,我们发现,当时间分辨率较小时(如GVS 手势),snn在GVS捕获的数据集上取得了显著的精度优势。 例如,dt≤10ms)。这表明,与连续rnn不同,事件驱动snn更适合提取稀疏特征,[29]中也指出了这一点。在 N-MNIST 这样的 DVS 转换数据集上,不同时间分辨率下尖峰事件的稀疏差距通常小于 DVS 捕获的数据集,从而降低了 SNN 的准确性优势。
 本质上,时间分辨率增加的影响并不总是积极的。如图8所示,随着dt的增长,时间坍缩也会损失一些尖峰,导致时间精度损失。为了研究负效应,我们对具有大dt值的N-MNIST进行了实验。为了消除dt变化时不同模拟时间长度(即T×dt)的影响,我们调整模拟时间步长以确保相同的模拟时间长度,即。此处固定T×dt=40ms。结果见表XI。当dt过度增加时,由于时间精度损失,精度降低。
本质上,时间分辨率增加的影响并不总是积极的。如图8所示,随着dt的增长,时间坍缩也会损失一些尖峰,导致时间精度损失。为了研究负效应,我们对具有大dt值的N-MNIST进行了实验。为了消除dt变化时不同模拟时间长度(即T×dt)的影响,我们调整模拟时间步长以确保相同的模拟时间长度,即。此处固定T×dt=40ms。结果见表XI。当dt过度增加时,由于时间精度损失,精度降低。
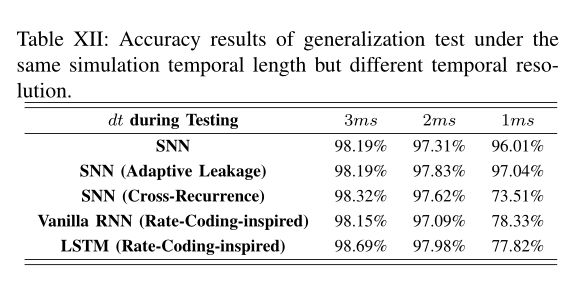
接下来,我们做了一个简单的实验来测试模型在不同时间分辨率下的泛化能力。我们在dt=3ms下在NMNIST上训练SNN模型、普通RNN模型(速率编码启发)和LSTM模型(速率编码启发),然后在dt={3ms,2ms,1ms}下测试训练的模型。此外,我们保持模拟时间长度与上述相同,此处固定T×dt=45ms。除非另有规定,泄漏系数等于0.3。
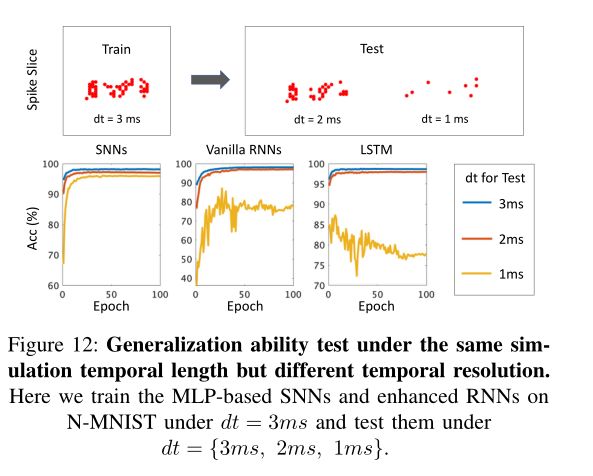
表XII报告了精度结果,训练曲线如图12所示。我们有两个观察结果:(1)在dt=2ms和dt=1ms条件下的测试失去了精度,并且随着dt变得更小(如dt=1ms),退化显著增加;(2) SNN模型表现出更好的泛化能力。具体而言,当在dt=1ms下进行测试时,SNN模型仅损失2.18%的准确性,而vanilla RNN模型和LSTM模型分别损失19.82%和20.87%的准确性,这远高于SNN模型的损失。
我们如下解释SNN的上述鲁棒性。首先,如前所述,由于事件驱动范式,SNN自然适合在较小的时间分辨率下处理稀疏特征。其次,与RNN中可训练的跨神经元递归权重不同,SNN使用具有受限权重的自神经元递归(即泄漏因子 − e − d t τ -e^{-\frac{dt}{\tau }} −e−τdt)。这种递归限制稳定了SNN模型,从而导致改进的泛化。 为了证明后一种预测,我们还使用可训练的跨神经元递归权重测试了SNN模型的性能,并在表XII中给出了结果。正如预期的那样,与RNN一样,泛化能力急剧下降 。这可能是由于引入可训练交叉神经元递归后,参数数量增加和动力学更复杂所致。此外,我们试图确定泄漏因子是否会影响SNN的泛化能力。在之前的所有实验中,泄漏因子固定为0.3;相比之下,我们通过仅固定τ但改变dt来进一步测试具有自适应泄漏因子的SNN模型。同样从表XII可以看出,自适应泄漏因子只是略微提高了鲁棒性。
D.损失函数和时间对比
在第四节-B中,我们观察到速率编码启发的损失函数可以提高DVScaptured数据集的准确性。在本小节中,我们将对这一现象进行更深入的分析。我们将神经形态视觉数据集的时间对比度定义为不同时间步的片之间的交叉熵。具体地说,我们将 S [ t , t + k ] S[t, t + k] S[t,t+k]表示为第t个时间步和第(t + k)个时间步之间的片。因此,在 S [ t x , t x + k ] S[t_x, t_x + k] S[tx,tx+k]和 S [ t y , t y + k ] S[t_y, t_y + k] S[ty,ty+k]之间存在交叉熵值,其中 t x t_x tx和 t y t_y ty可以是任意两个给定的时间步。这里我们定义交叉熵值为
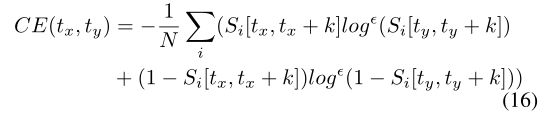
其中 i i i和 N N N分别为 S S S中元素的索引和个数。注意, l o g ϵ log^{\epsilon } logϵ是经过数值优化的log函数 l o g ϵ = l o g ( g ϵ ( x ) ) log^{\epsilon }=log(g^{\epsilon }(x)) logϵ=log(gϵ(x))。我们设置
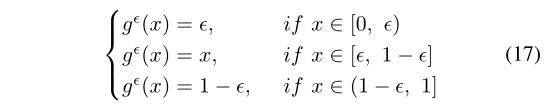
其中 ϵ = 1 e − 16 \epsilon= 1e−16 ϵ=1e−16是一个小常数。我们之所以进行上述优化,是因为S中的元素只能是{0,1}内的二进制值,这在通过log函数时可能会导致0或负无穷结果。然后,我们可视化我们使用的两个神经形态视觉数据集的交叉熵矩阵:DVS转换的NMNIST和DVS捕获的DVS手势,如图13所示。
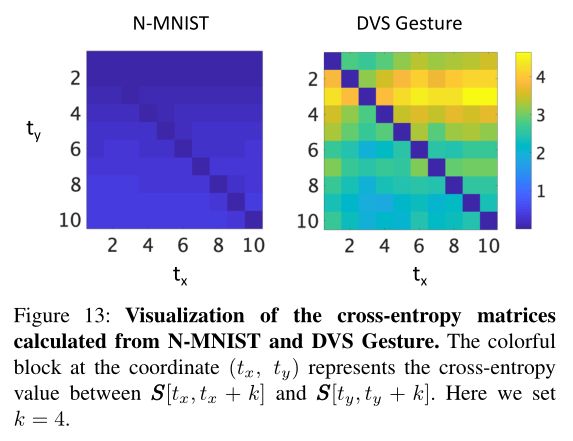
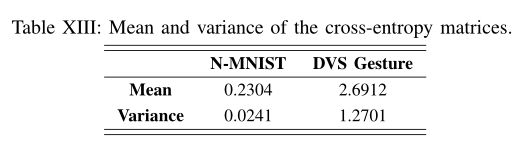
显然,可以看到dvs捕获数据集的时间对比度要远大于dvs转换数据集的时间对比度。这说明在dvs捕获的数据集中有更多的时间分量,而在dvs转换的数据集中不同时间步长的切片是紧密的。此外,我们还提供了由上述两个数据集推导出的交叉熵矩阵的统计数据,包括均值和方差。均值和方差的计算规则遵循统计学中的一般定义。如表XIII所示,它还表明,DVScaptured数据集的数据方差远远大于dvs转换数据集的数据方差,这与图13的结论一致。通过考虑不同时间步下的输出,式(15)中基于速率编码的损失函数能够提供所有时间步下的错误反馈,从而优化最终的识别性能。 上述定量分析可以很好地解释速率编码启发的损失函数在DVS Gesture上获得比N-MNIST上更多的精度提升的潜在原因。需要注意的是,当时间对比过大时,由于不同时间步梯度方向的发散,率编码损失函数的有效性可能会下降,这需要在未来更多的实践。
E.参数和操作数量
除了精度分析,我们还进一步考虑了模型运行过程中的内存开销和计算成本。对于计算复杂度,我们以一个有M个神经元的层为例。在正向传递中,我们用N个神经元计算当它将活动传播到下一个时间步和下一层时的操作;而在向后传递中,当它收到来自下一个时间步和下一层的梯度时,我们计算操作。注意,我们只计算矩阵运算,因为它们比向量和标量运算要复杂得多。对比如表14所示,主要由式(2)-(9)导出。显然,由于自神经元递归,SNN模型消耗更少的操作,并且由于spike格式,避免了向前传递中昂贵的乘法。此外,正向传递中的事件驱动计算可以进一步减少与归一化峰值速率成正比的所需操作。

另一方面,内存开销主要由参数的数量决定,特别是在仅使用边缘设备上的正向传递执行推断时。图14比较了snn、vanilla rnn和LSTM的模型参数个数。这里我们使用在DVS Gesture数据集上使用的模型进行说明。我们发现snn的参数量比rnn的参数量小得多。总体而言,snn与香草rnn和LSTM相比,分别只占用约80%和20%的参数
 有趣的是,尽管snn的操作和参数较少,但额外的膜势路径帮助它们实现了与具有复杂门的LSTM相当(在大时间分辨率下)甚至更好(在小时间分辨率下)的识别精度;同时,自神经元递归和限制性递归权使其更轻量化和鲁棒性。
有趣的是,尽管snn的操作和参数较少,但额外的膜势路径帮助它们实现了与具有复杂门的LSTM相当(在大时间分辨率下)甚至更好(在小时间分辨率下)的识别精度;同时,自神经元递归和限制性递归权使其更轻量化和鲁棒性。
F、关于音频数据的讨论
在前面的内容中,我们主要关注视觉数据集。实际上,具有时空成分的数据源的另一个重要分支是音频数据,它也被用于神经形态计算[52],[53]。为了稍微扩展这项工作的范围,我们在本小节中提供了一个关于音频数据集的额外实验。

我们选择口语数字[54]进行测试。网络结构为“Input-512FC-10”。超参数设置与N-MNIST上的相同,除了模拟时间步数,即T。我们在训练期间设置T=75,而在测试期间改变它以探索泛化。结果列于表XV。可以看出,普通RNN表现最差,而SNN表现最好。此外,SNN在该数据集上表现出更好的泛化能力,这与第IV-C节中的观察结果一致。
五、 结论
在这项工作中,我们进行了一项系统研究,以比较神经形态视觉数据集上的SNN和RNN,然后比较它们的性能和复杂性。为了使SNN和RNN具有可比性并提高公平性,我们首先从建模和学习角度识别它们之间的一些相似性和差异,然后统一数据集选择、时间分辨率、学习算法、损失函数、网络结构和训练超参数。
特别是,在SNN的速率编码方案的启发下,我们修改了RNN的主流损耗函数,以接近SNN的损耗函数;为了测试模型的鲁棒性和泛化,我们建议调整神经形态视觉数据集的时间分辨率。基于对N-MNIST(DVS转换数据集)和DVS手势(DVS捕获数据集)的一系列对比实验,我们在识别精度、特征提取、时间分辨率和对比度、学习泛化、计算复杂性和参数量方面获得了广泛的见解。为了更好的可读性,我们将有趣的发现总结如下:
-
SNN通常能够比普通RNN实现更好的准确性。然而,速率编码启发的损失函数可以提高RNN(尤其是LSTM)的精度,使其与SNN相当,甚至略好。
-
SNN的事件驱动范式使其更适合处理稀疏特征。因此,在具有稀疏尖峰事件的小时间分辨率的情况下,SNN具有明显的精度优势。
-
一方面,LSTM可以通过复杂的门记忆长期依赖性,而SNN的膜外电位路径也比香草RNN带来更长期的记忆;另一方面,DVS捕获数据集中切片的时间对比度远大于DVS转换数据集,因此DVS捕获的数据集的处理更依赖于长期记忆能力。这两方面可以解释为什么SNN和LSTM在DVS手势上显著优于普通RNN,而在N-MNIST上这一差距很小。
-
自神经元递归模式和SNN的受限递归权重大大减少了参数和操作的数量,从而提高了运行效率和模型泛化。
我们相信,上述结论将有助于未来在不同工作负载下的神经网络选择和设计。我们简单讨论几个例子。在DVS转换的数据集上,不同模型之间的精度差距很小,因此任何模型选择都是可以接受的。在DVS捕获的数据集上,我们不建议使用普通RNN,因为其准确性较低。当时间分辨率较大时,我们建议使用速率编码启发损失函数的LSTM;而当时间分辨率很小时,我们建议使用SNN。
如果我们需要一个紧凑的模型大小,我们总是建议SNN具有明显更少的参数和操作。
此外,还可以通过相互借鉴来改进模型。例如,可以通过引入更多的信息传播路径(如SNN中的膜电位路径)来进一步增强vanilla RNN;通过引入递归约束,LSTM可以变得更紧凑和鲁棒;SNN可以通过引入更多的门(如LSTM)来改进。甚至可以通过组合多种神经元来构建混合神经网络模型,从而利用不同模型的优点并缓解它们各自的缺陷。此外,我们主要关注视觉数据集,在这项工作中仅对音频数据进行了非常有限的探索。人们高度期望在广泛的任务中进行更广泛的实验。