【机器视觉学习笔记】双线性插值实现图片任意角度旋转(C++)
目录
- 原理
- 源码
-
- RotateImage_BilinearInterpolation
- 主函数
- 效果
- 与最近邻插值比较
-
- 原图
- 最近邻插值效果(局部)
- 双线性插值效果(局部)
- 完整源码
平台:Windows 10 20H2
Visual Studio 2015
OpenCV 4.5.3
原理

如图所示,我们需要求P点的像素值。我们已知了Q11、Q21、Q12、Q22、P的坐标。也知道Q11、Q21、Q12、Q22的像素值。所以先用关于X的单线性插值去分别计算R1、R2的像素值
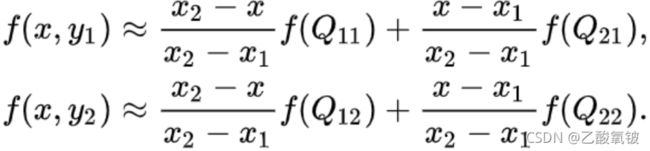
由以上思路可化简得到如下式子。 I x I_x Ix为该点上的像素值或灰度值

源码
RotateImage_BilinearInterpolation
Mat RotateImage_BilinearInterpolation(Mat src, double angle)
{
int x0, y0, x1, y1;
angle = angle * 3.1415926535897932384626433832795 / 180;
int dx = abs((int)src.cols*cos(angle)) + abs((int)src.rows*sin(angle));
int dy = abs((int)src.cols*sin(angle)) + abs((int)src.rows*cos(angle));
Mat dst(dy, dx, CV_8UC3, Scalar(0)); //创建新图像
for (x1 = 0; x1 < dst.cols; x1++)
{
for (y1 = 0; y1 < dst.rows; y1++)
{
double fx0, fy0;
double fx1, fy1;
double R;
double sita, sita0, sita1;
int x01, y01;
int x02, y02;
int x03, y03;
int x04, y04;
double p, q;
//将图片中点设为坐标原点
fx1 = x1 - dst.cols / 2;
fy1 = y1 - dst.rows / 2;
R = sqrt(fx1 * fx1 + fy1 * fy1); //极径
sita = angle;
sita1 = atan2(fy1, fx1); //新点极角
sita0 = sita1 + sita; //旧点极角
//旧点直角坐标(中点为坐标原点)
fx0 = R * cos(sita0);
fy0 = R * sin(sita0);
//旧点直角坐标(坐标原点在角上)
x0 = fx0 + src.cols / 2 + 0.5;
y0 = fy0 + src.rows / 2 + 0.5;
x01 = (int)(fx0 + src.cols / 2);
y01 = (int)(fy0 + src.rows / 2);
x02 = x01 + 1;
y02 = y01;
x03 = x01 + 1;
y03 = y01 + 1;
x04 = x01;
y04 = y01 + 1;
p = (fx0 + src.cols / 2) - x01;
q = (fy0 + src.rows / 2) - y01;
if (x01 >= 0 && x03 < src.cols && y01 >= 0 && y03 < src.rows)
{
for (int i = 0; i < 3; ++i)
dst.at<Vec3b>(Point(x1, y1))[i] = src.at<Vec3b>(Point(x01, y01))[i] * (1 - p) * (1 - q) + src.at<Vec3b>(Point(x02, y02))[i] * p * (1 - q) + src.at<Vec3b>(Point(x03, y03))[i] * p * q + src.at<Vec3b>(Point(x04, y04))[i] * (1 - p) * q;
}
else if (x0 >= 0 && x0 < src.cols && y0 >= 0 && y0 < src.rows)
dst.at<Vec3b>(Point(x1, y1)) = src.at<Vec3b>(Point(x0, y0));
else
dst.at<Vec3b>(Point(x1, y1)) = 0;
}
}
return dst;
}
主函数
int main(int argc, char * argv[])
{
Mat src;
src = imread("D:\\Work\\OpenCV\\Workplace\\Test_1\\4.jpg");
imshow("原图", src);
imshow("输出", RotateImage_BilinearInterpolation(src, 45));
waitKey(0);
return 0;
}
效果
与最近邻插值比较
原图
最近邻插值效果(局部)
双线性插值效果(局部)
完整源码
#include