时间序列分析之:函数分解decompose
时间序列分析——函数分解
第一篇 函数分解
函数分解decompose
文章目录
- 时间序列分析——函数分解
- 前言
- 一、函数分解是什么?
- 二、建立分解函数
-
- 1.功能
- 2.测试函数
- 总结
前言
这几天一直在深思,如何建立一个和实际比较贴切的金融模型,能反映现实生活?比如我们听到国家又放水了,我们可以预期物价又得上涨了,但是如何通过模型来反映这种相关关系呢?
伙伴杨RC说用EXCEL建了个模型来预测本期深圳车牌竞价,以达到最小的成本拍到车牌,这个想法不错,Good lucky to my brother。
简单的模型可以用EXCEL,复杂的模型就得使用python。
随着人工智能的不断发展,机器学习越来越重要,我们的目标是让机器进行数据分析,发现一些特性和趋势。本文就介绍时间序列分析的基础。
一、函数分解是什么?
说白了就是拆分信号。刚好函数分解和我们想要建立的模型有点吻合:environment大趋势 + company的周期性波动 + market的高斯扰动。
当然后续我们会引入相关性分析、情感分析等要素。
二、建立分解函数
1.功能
分解函数成三部分:趋势、周期、和剩余部分(一般指噪声,均值为0)
分解就是将时序数据分离成不同的成分,分解有:长期趋势Trend、季节性seasonality和随机残差residuals
返回包含三个部分 trend(趋势部分) , seasonal(季节性部分) 和residual (残留部分)
传入:一个序列,可以是时间序列
输出:趋势、周期、和剩余部分 三部分
函数详解地址:链接
所以,我们建立一个python文件,命名为compose.py ,方便后续函数进行调用。
代码如下:
# 功能:分解函数成三部分:趋势、周期、和剩余部分(一般指噪声)
# 分解就是将时序数据分离成不同的成分,分解有:长期趋势Trend、季节性seasonality和随机残差residuals
# 返回包含三个部分 trend(趋势部分) , seasonal(季节性部分) 和residual (残留部分)
# 创建时间:2021-01-15
# 传入:一个序列
# 输出:趋势、周期、和剩余部分 三部分
# 函数详解地址:https://machinelearningmastery.com/decompose-time-series-data-trend-seasonality/
from statsmodels.tsa.seasonal import seasonal_decompose
import matplotlib.pyplot as plt
def decompose(timeseries,frequence):
# 传入数列和频率数
# 返回包含三个部分 trend(趋势部分) , seasonal(季节性部分) 和residual (残留部分)
# statsmodels也支持两类分解模型,加法模型和乘法模型,model的参数设置为"additive"(加法模型)和"multiplicative"(乘法模型)。
# period:int, optional,系列的时期。如果x不是pandas对象或x的索引没有频率,则必须使用。如果x是具有时间序列索引的pandas对象,则覆盖x的默认周期性
# decomposition = seasonal_decompose(timeseries,model='multiplicative',freq=frequence)
decomposition = seasonal_decompose(timeseries, model='additive', freq=frequence)
trend = decomposition.trend
seasonal = decomposition.seasonal
residual = decomposition.resid
# 画图参数
fig = plt.figure()
ax1 = fig.add_subplot(411)
ax1.plot(timeseries, label='Original')
ax1.legend(loc='best')
ax2 = fig.add_subplot(412)
ax2.plot(trend, label='Trend')
ax2.legend(loc='best')
ax3 = fig.add_subplot(413)
ax3.plot(seasonal, label='Seasonality')
ax3.legend(loc='best')
ax4 = fig.add_subplot(414)
ax4.plot(residual, label='Residuals')
ax4.legend(loc='best')
fig.tight_layout()
plt.show(block=False)
return trend, seasonal, residual
2.测试函数
我们先合成一个:趋势 + 周期性波动 + 高斯扰动的函数,测试我们的compose函数能否成功分解。
测试函数如下:
import matplotlib.pyplot as plt
import numpy as np
import math
from math import *
import pandas as pd
from decompose import *
plt.rcParams['font.sans-serif']=['SimHei'] #解决中文乱码
plt.rcParams['axes.unicode_minus'] = False
xtime = np.arange(1,1000,1)
xnorm = xtime/len(xtime)
queshi = 2*xnorm +1
fig1 = plt.figure()
ax1 = fig1.add_subplot(412)
ax1.plot(xtime,queshi, label='趋势')
ax1.legend(loc='best')
zouqi = [sin(x*20*math.pi) for x in xnorm]
ax2 = fig1.add_subplot(413)
ax2.plot(zouqi, label='周期')
ax2.legend(loc='best')
noize = 0.02*np.random.normal(size=xtime.size)
ax3 = fig1.add_subplot(414)
ax3.plot(noize, label='噪声')
ax3.legend(loc='best')
signal = queshi+zouqi+noize
ax4 = fig1.add_subplot(411)
ax4.plot(signal, label='合成信号')
ax4.legend(loc='best')
fig1.tight_layout()
plt.show(block=False)
signal = pd.Series(signal).astype('float')
trend , seasonal, residual = decompose(signal,frequence = 200)
plt.show()
生成合成函数如下:

分解函数结果如下:
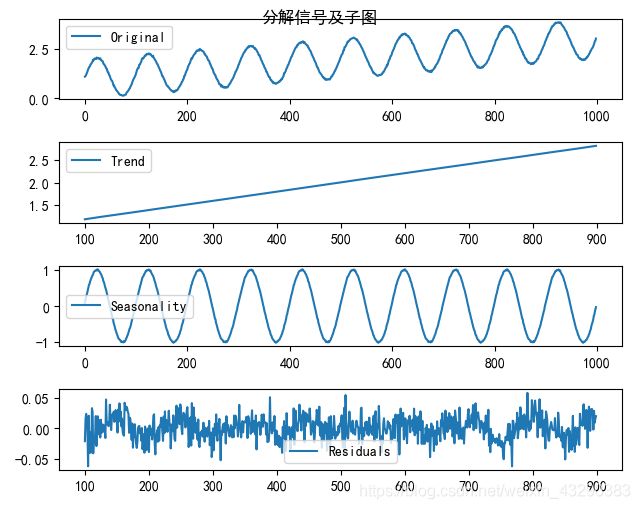
可以看出完全分解还原了我们模拟的信号。
这里需要注意的是:我们提前知道了输入序列的周期,所以可以完美拆分,如果我们把周期信号填错了,那么结果又会出现非常大的偏差。
比如本次合成信号的周期是100的整数倍,如果我们输成了150,那会是怎么样?
signal = pd.Series(signal).astype('float')
trend , seasonal, residual = decompose(signal,frequence = 150)
分解结果:
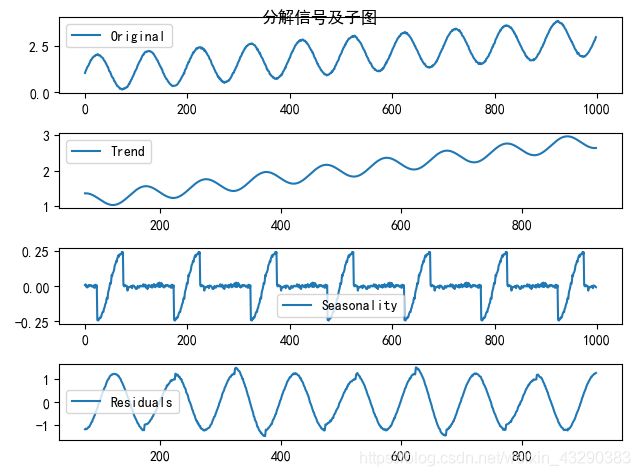
可以看到,此时趋势不同了,周期函数的权重降低了,本该是噪音的信号,现在变得很强。模型已经开始失真。
如果我们用33这个周期去测试,结果会是怎样?
trend , seasonal, residual = decompose(signal,frequence = 33)
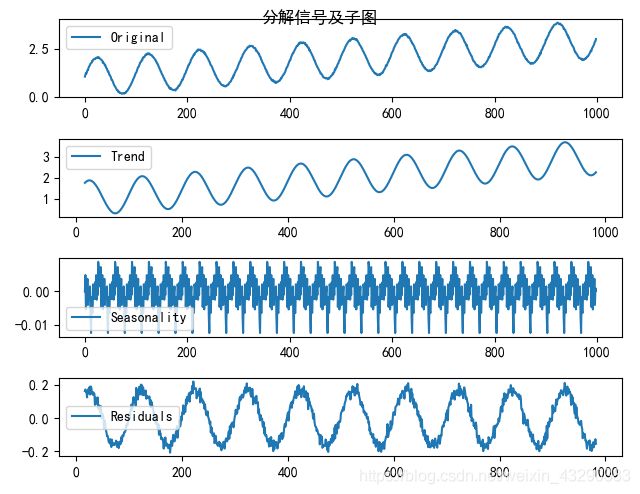
结果如下:周期信号基本成了噪音,趋势信号已经糅合和其他信号,市场扰动也不明显了。
因此对信号的周期的确定,有至关重要的作用。
下篇我们将探寻如何寻找时间序列的周期。
总结
每个G民都觉得自己是G神,实际上只是布朗运动中的一份子,高斯白噪声中的一个噪点而已。
没有谁能预测未来。未来是属于未来的。