FastReID A PyTorch ToolBox for General Instance ReIdentification 论文学习

Abstract

通用的实例 ReID 在计算机视觉领域是非常重要的一个任务，可许多应用中都有使用，如行人/车辆重识别、人脸识别、野生动物保护、商品追溯等。为了满足日益增长的需求，本文介绍了一个在京东广泛应用的软件系统 — FastReID。高度模块化和可扩展设计使之使用起来很方便。友好的管理系统配置和工程部署功能让从业者能很快地在应用中部署模型。作者实现了一些 SOTA 的工程，包括行人重识别、跨域重识别和车辆重识别，计划将这些在多个基准上预训练的模型开放出来。FastReID 是目前为止最通用、性能最优的工具库，支持单个或多个GPU服务器，你可以很容易地复现本文提到的结果。模型和代码位于：https://github.com/JDAI-CV/fast-reid。

1. Introduction

通用实例重识别是一个以实例为中心的 AI 技术，其目的是在大量的视频文件中找到某一个人/车辆/人脸/物体。它促成了各类应用的实现，以前这些应用需要大量痛苦、无聊的观看视频，包括在电视连续剧中找到某个演员的视频画面，从监控视频中找到一个走失的儿童，城市监控系统中一个可疑的车辆。此外，通用的实例重识别技术也会用在电商网站上，商品安全的商品追踪以及野生动物保护领域。然而在学术研究和工业落地之间一直存在着鸿沟，很难将学术成果快速落地到生产中。

为了促进通用实例重识别技术的发展，作者开放了一个统一的实例重识别库，叫做 FastReID。它具备很高的模块化、扩展性设计，使研究人员和从业者能迅速地将他们设计的模块插入一个重识别系统中，而无需重写代码，将科研想法转变为生产模型。管理系统配置让它更加灵活、可扩展，可很容易地应用到其它领域，如人脸识别和图像检索。作者提供了多个基准上训练的预训练模型，比如行人重识别、跨域重识别、车辆重识别、部分行人重识别，在将来还会放出人脸识别和目标检索模型。

最近，FastReID 已成为 JD AI 研究院广泛应用的开源库。作者会持续优化它，增加新的功能。

2. Highlights

FastReID 提供了训练、测试、微调和部署一整套工具包。此外，FastReID 也提供了强大的基线模型，能够在多个任务上取得优异的表现。

模块化和可扩展设计。在 FastReID 中，作者引入了一个模块化设计，用户可以在重识别系统中任一部分中插入自定义的模块。因此，研究员和从业者可快速实现他们的想法，无需写多少代码。

图1. FastReID 库的流程

管理系统配置。FastReID 用 PyTorch 实现，可在多个GPU服务器上快速训练。模型定义、训练和测试用 YAML 文件编写。FastReID 支持许多的选项，如主干网络、head聚合层和损失函数、训练策略。

更丰富的评价系统。目前，许多研究员只使用 CMC 评价指标。为了满足模型部署的需要，FastReID 提供了更多丰富的评价指标，如 ROC和mINP，能更好地反映模型的表现。

工程部署。太深的模型很难部署在边缘设备上，因为推理太耗时了。FastReID 使用知识蒸馏模块来得到一个准确而高效的轻量级模型。同样，FastReID 提供了一个转换工具，PyTorch$\to$Caffe 以及PyTorch$\to$TensorRT，进行快速的模型部署。

预训练模型。FastReID 提供了 SOTA 的推理模型，包括行人重识别、局部重识别、跨域行人重识别和车辆重识别。作者计划开放所有的这些模型。FastReID 很容易就可扩展到人脸识别和通用目标检索。

3. Architecture

这一部分，作者在图1中展示了其架构。整体架构包括4个模块：图像预处理、主干网络、聚合和head。

3.1 图像预处理

搜集来的图像有不同的大小，我们首先将它们缩放到同样的尺寸。然后将这些图像做为一个batch，输入进网络。为了得到一个更加鲁棒的模型，翻转会将原图像做镜像，让数据更多样。随机擦除、随机裁剪会随机选择图像中的一个矩形区域，用随机数、0值、图像等来填充里面的像素，避免模型过拟合，对遮挡更鲁棒。自动增广是基于 AutoML 的一种技术，可提升特征表示的鲁棒性。它使用自动搜索算法找到融合的策略，如平移、旋转、裁剪。

3.2 主干网络

主干就是推理出图像特征图的网络，比如没有最后平均池化层的 ResNet。FastReID 实现了3种主干，包括 ResNet、ResNeSt、ResNeXt。作者也增加了注意力 Non-local 模块和实例批归一化（IBN）模块，学习更鲁棒的特征。

3.3 Aggregation

聚合层目的是将主干网络的特征图聚合为一个全局特征。作者介绍了4种聚合方法：最大池化、平均池化、GeM 池化和注意力池化。池化层的输入是$\mathbf{M}\in {\mathbb{R}}^{W\times H\times C}$，输出是$\mathbf{f}\in {\mathbb{R}}^{1\times 1\times C}$，$W,H,C$分别是宽度、高度和通道数。对于最大池化、平均池化和 GeM池化而言，全局向量$\mathbf{f}=[f_1,f_c,...,f_C]$ 分别是：

$$\text{Max Pooling:}{f}_c=\underset{x\in {\mathbf{X}}_c}{\max }x\text{\hspace{1em}(1)}$$

$$\text{Avg Pooling:}{f}_c=\frac{1}{|{\mathbf{X}}_c|}\sum _{x\in {\mathbf{X}}_c}x\text{\hspace{1em}(2)}$$

$$\text{Gem Pooling:}{f}_c=(\frac{1}{|{\mathbf{X}}_c|}\sum _{x\in {\mathbf{X}}_c}{x}^{\alpha }{)}^{\frac{1}{\alpha }}\text{\hspace{1em}(3)}$$

$$\text{Avg Pooling:}{f}_c=\frac{1}{|{\mathbf{X}}_c\ast {\mathbf{W}}_c|}\sum _{x\in {\mathbf{X}}_c,w\in {\mathbf{W}}_c}w\ast x\text{\hspace{1em}(4)}$$

其中$\alpha$为控制系数，${\mathbf{W}}_c$是 softmax 注意力权重。

3.4 Head

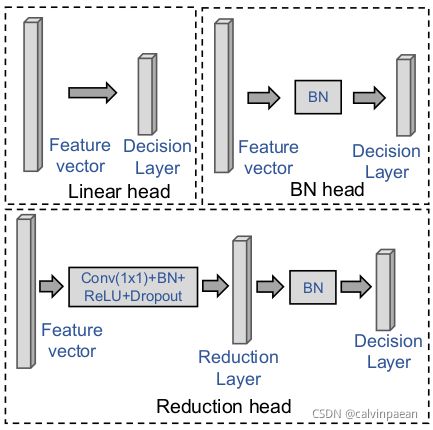
Head 用于聚合模块输出的全局向量，包括批归一化 head、线性 head和 Reduction head。图3列出了这三种 head，线性 head 只包括一个决策层，BN head包括一个 BN 层和一个决策层，Reduction head 包括 conv+bn+relu+dropout 操作、一个 reduction 层和一个决策层。

图3. FastReID 中不同的 Heads

Batch Norm 用于解决内部协变量偏移（internal covariate shift）问题，因为用易饱和的非线性函数训练模型很困难。给定一个batch的特征向量$\mathbf{f}\in {\mathbb{R}}^{m\times C}$（$m$是该batch内的样本数），然后 BN 特征向量${\mathbf{f}}_{bn}\in {\mathbb{R}}^{m\times C}$计算如下：

$$\{\begin{array}{rl}\mu & =\frac{1}{m}\sum _{i=1}^m{\mathbf{f}}_i,\\ {\sigma }^2& =\frac{1}{m}\sum _{i=1}^m({\mathbf{f}}_i-\mu {)}^2,\\ z& =\gamma \cdot \frac{\mathbf{f}-\mu }{\sqrt{{\sigma }^2+ϵ}+\beta }\end{array}\text{\hspace{1em}(5)}$$

其中$\gamma ,\beta$是可训练的缩放和偏移参数，$ϵ$是一个常数，加在 mini-batch 的方差之上，保证数值稳定。

Reduction 层目的是将高维特征变为低维特征，如 2048-dim $\to$ 512-dim。

决策层输出不同类别的置信度以区分不同的类别，进行后续的模型训练。

4. 训练

4.1 损失函数

FastReID 提供了4种损失函数。

交叉熵损失 通常用在多选一的分类问题中，定义为：

$${\mathcal{L}}_{ce}=\sum _{i=1}^C{y}_i\log {\hat{y}}_i+(1-y_i)\log (1-{\hat{y}}_i),\text{\hspace{1em}(6)}$$

其中${\hat{y}}_i=\frac{e^{{\mathbf{W}}_i^T\mathbf{f}}}{{\sum }_{i=1}^C{e}^{{\mathbf{W}}_i^T\mathbf{f}}}$。交叉熵损失让预测的对数值趋近于 ground truth。它让最大的对数值和其它值的差距变大，再加上梯度是有界的，就降低了模型调节的能力，造成模型对预测值过于自信，从而导致过拟合。为了构建一个鲁棒的模型，Label smoothing 被谷歌大脑提了出来，解决该问题。它让倒数第二层的激活值趋近于正确类别，而错误类别的距离则是相等的。这样交叉熵损失中的 $\mathbf{y}$ 就可写作：$y_i(j=c)=1-\delta$，$y_i(j\ne c)=\frac{\delta }{C-1}$。

Arcface 损失将笛卡尔坐标映射到超球面坐标。它将对数变换为${{\mathbf{W}}_{\mathbf{i}}}^T\mathbf{f}=\Vert {\mathbf{W}}_i\Vert \Vert f\Vert \cos {\theta }_i$，其中${\theta }_i$是权重${\mathbf{W}}_{\mathbf{i}}$和特征$\mathbf{f}$的角度。它通过 L2 归一化将单个权重$\Vert {\mathbf{W}}_{\mathbf{i}}\Vert =1$，同样将 embedding 特征 $\mathbf{f}$ 固定，然后缩放它为$s$，这样$\hat{y}=\frac{e^{s\cos {\theta }_i}}{{\sum }_{i=1}^C{e}^{s\cos {\theta }_i}}$。为了同时增强类内紧凑度和类间差异，Arcface 增加了一个额外的角度距离惩罚项$m$。这样${\hat{y}}_i=\frac{e^{s\cos {\theta }_i+m}}{e^{s\cos {\theta }_i+m}+{\sum }_{i=1,i\ne c}^{C-1}{e}^{s\cos {\theta }_i}}$。

Circle 损失。Circle损失的推导过程没有介绍，可参考[10]。

Triplet 损失 确保某个人的所有图像足够接近，在特征空间内，让某个人的图像$x_i^a$(anchor)接近该人的其它图像$x_i^p$(positive)，而距离其他人的图像$x_i^n$(negative)足够远。因此，我们希望$D(x_i^a,x_i^p)+m<D(x_i^a,x_i^n)$，其中$D(:,:)$用于计算两张行人图像的距离。然后$N$个样本的 Triplet loss 的定义为：${\sum }_{i=1}^N[m+D(g_i^a,g_i^p)-D(g_i^a,g_i^n)]$，其中$m$是加在一对正负样本上的 margin。

4.2 训练策略

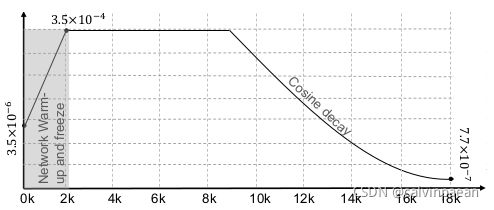
图4 显示了训练策略，包括许多的训练技巧，如不同迭代时的学习率、网络预热和冻结。

学习率预热 帮助减缓网络在初始阶段过早地过拟合。它也能帮助保持模型的稳定性。所以，作者给了一个非常小的学习率，比如训练初始时$3.5\times 10^{-5}$，然后在2000个迭代过程中逐渐增加。在2000到9000次迭代时，学习率维持在$3.5\times 10^{-4}$。9000次迭代后，学习率通过余弦策略从$3.5\times 10^{-4}$衰退到$7.7\times 10^{-7}$。在18000次迭代时，训练结束。

图4. 学习率曲线

主干网络冻结。为了让分类网络满足我们任务的需求，作者在 ImageNet 上预训练模型。通常，我们会在 ResNet 之上加一个分类器，然后分类器参数随机初始化。为了更好地初始化参数，作者只训练了分类器参数，在前2000个迭代时冻结了网络其余参数，不更新其参数。2000次后，释放这些参数，让它们进行端到端的训练。

5. 测试

5.1 距离度量

FastReID 实现了欧式距离和余弦距离。作者也实现了一个局部匹配方法：深度空间重建（DSR）。

深度空间重建。假设有两张行人图像$x$和$y$。将$x$的主干网络的空间特征图标记为$\mathbf{x}$，其维度是$w_x\times h_x\times d$，$y$的特征图维度是$w_y\times h_y\times d$。然后将$N$个位置的$N$个空间特征聚合，得到矩阵$\mathbf{X}=[{\mathbf{x}}_n{]}_{n=1}^N\in {\mathbb{R}}^{d\times N}$，其中$N=w_x\times h_x$。同样，作者构建了一个图像库特征矩阵$\mathbf{Y}=\{{\mathbf{y}}_m{\}}_{m=1}^M\in {\mathbb{R}}^{d\times M}$，其中$M=w_y\times h_y$。然后${\mathbf{x}}_n$能够在$\mathbf{Y}$中找到最相似的特征，以及其匹配的得分$s_n$。所以，作者尝试得到$\mathbf{X}$的所有特征关于$\mathbf{Y}$的相似得分，最终的匹配得分定义为$s={\sum }_{n=1}^N{s}_n$。

5.2 后处理

FastReID 实现了两个再排序方法：K-reciprocal coding 和 Query Expansion。

Query Expansion。给定一个查询图片，用它找到$m$张相似图片。查询特征的定义是${\mathbf{f}}_q$，$m$个相似特征定义为${\mathbf{f}}_g$。然后将验证了的图库特征和查询特征求平均，构建出一个新的查询特征。所以新的查询特征${\mathbf{f}}_{newq}$的定义是：

$${\mathbf{f}}_{newq}=\frac{{\mathbf{f}}_q+{\sum }_{i=1}^m{\mathbf{f}}_g^{(i)}}{m+1}\text{\hspace{1em}(7)}$$

然后新的查询特征${\mathbf{f}}_{qnew}$就可用于后续的图像检索。QE可以很容易地应用在实际场景中。

5.3 Evaluation

对于表现评价，作者使用了行人重识别领域中的标准的度量，即累积匹配曲线（CMC）和平均精度（mAP）。此外，作者也增加了2个度量：re-ceiver operating characteristic (ROC) curve 和 mean in-verse negative penalty (mINP)。

5.4 可视化

作者提供了多个排序列表工具来呈现检索结果。

6. 部署

通常模型越深，性能越好。但是，模型太深了就不容易在边缘设备上部署，因为1) 推理很耗时，2）AI芯片上很难实现某些层。考虑到这些原因，作者实现了知识蒸馏的方法来得到高精度、高效率的轻量级模型。

图5.。 知识蒸馏模块

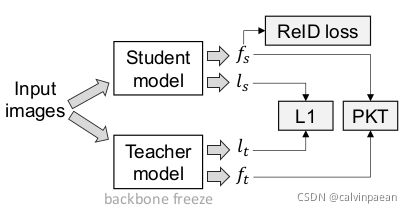
如图5，给定在 ReID 数据集上的预训练学生模型和预训练教师模型，教师模型更深一些，使用了 non-local 模块、IBN 模块和其它技巧。学生模型很简单、层浅。作者采用了双流方式来训练学生模型，将教师主干冻结。学生和教师模型分别输出分类器logit ${\mathbf{l}}_s,{\mathbf{l}}_t$及特征${\mathbf{f}}_s,{\mathbf{f}}_t$。我们希望学生模型学习教师模型的分类能力，logit 学习可定义为：

$${\mathcal{L}}_{logit}={\Vert {\mathbf{l}}_s-{\mathbf{l}}_t\Vert }_1\text{\hspace{1em}(8)}$$

为了确保学生模型和教师模型在特征空间的分布一致，作者使用了基于KL散度的概率知识迁移模型，从而优化学生模型：

$$\{\begin{array}{rl}{\mathcal{L}}_{PKT}& =\sum _{i=1}^N\sum _{j=1,i\ne j}^N{p}_{j|i}\log (\frac{p_{j|i}}{p_{i|j}}),\\ p_{i|j}& =\frac{K({\mathbf{f}}_s^i,{\mathbf{f}}_s^j)}{{\sum }_{j=1,i\ne j}^{N}K({\mathbf{f}}_s^i,{\mathbf{f}}_s^j)},\\ p_{j|i}& =\frac{K({\mathbf{f}}_t^i,{\mathbf{f}}_t^j)}{{\sum }_{j=1,i\ne j}^{N}K({\mathbf{f}}_t^i,{\mathbf{f}}_t^j)}\end{array}\text{\hspace{1em}(9)}$$

其中$K(:,:)$是余弦相似度。

同时，学生模型需要 ReID 损失${\mathcal{L}}_{reid}$来优化整个网络。因此，总的损失是：

$${\mathcal{L}}_{kd}=logit+\alpha {\mathcal{L}}_{PKT}+{\mathcal{L}}_{reid}.\text{\hspace{1em}(10)}$$

完成训练后，${\mathbf{f}}_s$用于推理。

作者在 FastReID 库中也提供了模型转换工具（Pytorch $\to$Caffe，Pytorch $\to$TensorRT）。