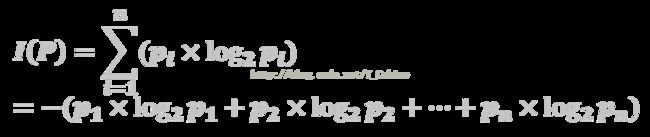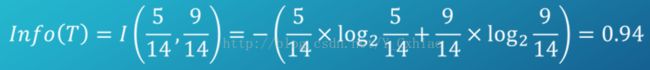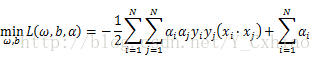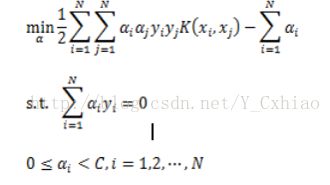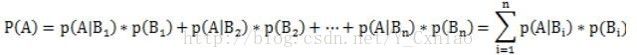数据科学学习笔记8 --- 分类（有监督的学习）

数据挖掘十大算法中的C4.5 和 CART（分类和回归树）算法都是决策树算法。其他常用的决策树算法有C5.0、Fuzzy C4.5、SLIQ（Mehta 1996）、SPRINT（Shafer 1996）等。

1 决策树算法

· 决策树是一种由节点和有向边组成的层次结构，如下图所示，树中包含三种节点

· 根节点（Root node），没有入边，但有零条或者多条出边

· 内部节点（Internal node），有一条入边和两条或多条出边

· 叶子节点（Leaf node），又叫终止节点（Terminal node），只有一条入边，没有出边

· 在决策树中，每个叶子节点都有一个类标号。非叶子结点（包括根节点和内部节点），包含属性测试条件，用于分开具有不同特性的记录。

· 决策树算法的生成过程包括：树构造（Tree building）、树剪枝（Tree pruning）

（1）树构造阶段，决策树采用自顶向下的递归方式从根节点开始在每个节点上按照给定标准选择测试属性，然后按照相应属性的所有可能取值向下建立分支、划分训练样本，直到一个节点上的所有样本都被划分到同一个类，或者某一个节点中的数量样本低于给定值时为止

（2）树剪枝阶段，构造过程得到的并不是最简单、最紧凑的决策树，因为许多分枝反映的可能是训练数据中的噪声或孤立点。树剪枝过程主要检测和去掉这种分枝，以提高对未知数据集进行分类时的准确性

· 决策树算法应用非常广泛，其独特的优点包括：

（1）是一种非参数方法，不要求任何先验假设，不假定类和其他属性服从一定的概率分布

（2）决策树的训练时间相对较少，即使训练集很大，也可以快速的构建分类模型

（3）决策树的分类模型是树状结构，简单直观，符合人类的理解方式

（4）可以将决策树中到达每个叶结点的路径转换为 if --- then 形式的分类规则，这种形式更有利于理解

（5）对于噪声的干扰具有较好的鲁棒性，训练数据可以包含错误或缺少属性值

· 决策树算法的缺点：

（1）决策树算法属于贪心算法，只能是局部最优

（2）对于何时停止剪枝需要由较准确的把握

· 决策树的应用，是通过对未分类实例的属性与决策树比较，实现对未分类实例的类别判定

· 决策树算法适用于用 属性-键值对 表示的实例

· 决策树是利用信息论原理对大量样本的属性进行分析和归纳产生的

2. 信息论基础知识

（1）信息量

· 若存在n个相同概率的消息，则每个消息的概率 p = 1/n ，一个消息传递的信息量为 -Log2(1/n) （即基数为2的概率的对数）。

· 例如，有32个相同概率的消息，则每个消息传递的信息量为 -Log2(1/32) = 5 ，即每个消息传递的信息量为5，需要用5个比特来表示1个消息

（2）熵

· 若有n个消息，其给定概率分布为 P = ( p1, p2, ... , pn)，则由该分布传递的信息量称为 P 的熵，记为（第一行少了一个负号）

（3）分类集合信息量

· 若一个记录集合T根据类别属性的值被分为互相独立的类C1，C2，...，Ck，则识别T的一个元素属于哪个类所需要的信息量为 Info(T) = I(P)，其中 P 为C1,C2,...Ck的概率分布，即

· 若现根据非属性类别 X 的值将 T 分成集合T1,T2,...Tk，则在已得到的属性X的之后确定T中一个元素类的信息量（也称期望熵）为：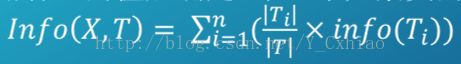

（4）信息增益度

· 信息增益度是两个信息量之间的差值，其中之一是要确定T中元素类别的信息量，另一个信息量是在已得到的属性X的值后需确定的T中元素类别的信息量，信息增益度公式为

3. ID3算法（Iterative Dichotomic version3）

· ID3 算法采用信息增益度作为属性划分的衡量标准，从而实现对数据的归纳分类。其中，训练集中的记录可表示为（V1,V2,...,Vn；C），其中 Vi 表示属性值，C 表示类标签

· ID3 算法计算每个属性的信息增益度，并总是选取具有最高增益度的属性作为给定集合的测试属性。对被选取的测试属性创建一个节点，并以该节点的属性标记，对该属性的每个值创建一个分支，据此划分样本

· ID3 算法过程如下：

    · 输入：样本集合S，属性集合A

    · 输出：ID3决策树

    · （1）若所有种类的属性都处理完毕，返回；否则，执行（2）

    · （2）计算出信息增益最大属性a，把该属性作为一个节点。

    · （3）对属性a的每个可能的取值v，执行下一步操作

    ·     i.  将所有属性a的值为v的样本作为S的一个子集Sv；

    ·     ii. 生成属性集合 AT = A - {a}；

    ·     iii. 以样本集合Sv和属性集合AT为输入，递归执行ID3算法

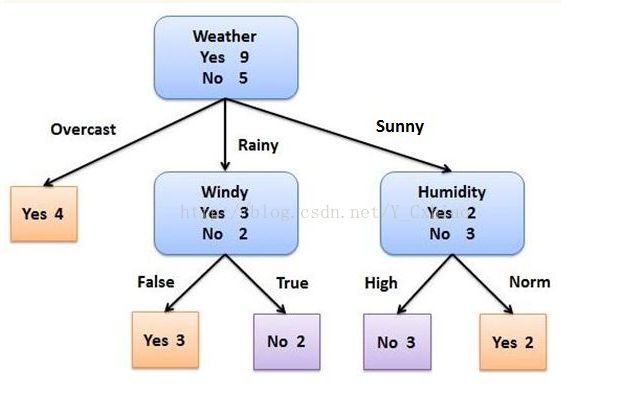
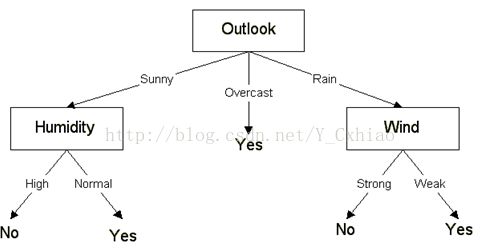
下面以上图为例说明算法过程。

在给出的样本数据中，“Play Ball”属性包含  9 个yes和 5 个no，则对应于该属性的期望信息（熵）为：

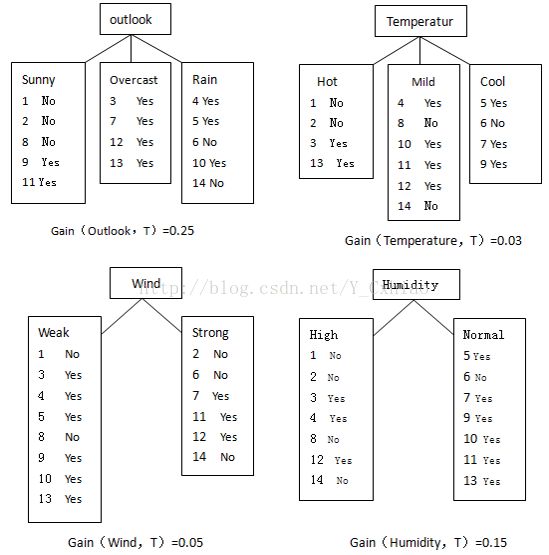
再根据OutLook的信息，分别计算

· 此时，具有最高的信息增益度的属性为Outlook属性，以该属性为节点进行分支。Outlook属性中有3个取值，分别为Sunny，Overcast，Rain，分别分别对应3个分支，将数据集划分为3个子集，S(sunny), S(overcast), S(rain)

· 在Sunny分支下，递归调用（S(sunny)，R - Outlook，C）分别计算得到Temperature属性的信息增益度为0.57，Humidity属性的信息增益度为0.97，Wind属性的信息增益度为0.02.因此，在此分支下再以Humidity属性对子集S(sunny)进行划分，得到子集SS(high)和SS(normal)，这两个子集的所有样本都属于同一类别，因此停止树的分裂，添加两个叶子节点，并写上子集的类别即可。最终的决策树如下图

· 在生成决策树以后，可以方便的提取决策树描述的知识，并表示成 if - then 形式的分类规则。沿着根节点到叶子节点每一条路径对应一条决策规则。如 if { Outlook = Sunny , Humidity = High } , then { Play ball = No }.

· 在生成决策树的过程中，除了要选择测试属性还要判断是否停止树的分裂，如在得到子集SS(high)和SS(normal)后停止了树的分支构造。停止树的分裂的条件如下所示，只要满足以下三个条件中的1条，即可停止树的分支构造。

    · i. 子集中的所有记录属于同一类树时

    · ii. 所有的记录具有相同的属性值

    · iii. 提前终止树的分裂

· ID3算法在实际应用中存在一些问题。如在选择根节点和内部节点中的分支属性时采用信息增益度作为评价标准。信息增益度的缺点是倾向于选择取值较多的属性，但在有些情况下这类属性可能不会提供太多有价值的信息。另外，ID3算法只能对离散型属性的数据集构造决策树。而在ID3的基础上Quinlan提出了C4.5算法（泛指基本的C4.5、C4.5-nopruning以及拥有多重特性的C4.5-rules等诸多变体的一套算法）

4. C4.5算法

· 继承了ID3算法，并在以下几个方面对ID3算法进行了改进

（1）用信息增益率来选择最佳分裂属性，弥补了用信息增益选择属性时偏向选择取值多的属性的不足；

（2）在树构造过程中进行剪枝；

（3）能够完成对连续属性的离散化处理；

（4）能够对不完整数据进行处理。

①。信息增益率

C4.5算法并不是直接选择增益率最大的，而是使用了一种启发式的方法：先从候选划分属性中找出信息增益高于平均水平的，再从其中选择增益率最高的

②。处理连续属性值

· ID3算法把属性值假设为离散型，但是实际生活中很多属性是连续值。C4.5算法对连续属性的处理有两种办法，一种是基于信息增益度的，另一种则是基于最小描述长度原理。

· 基于信息增益的连续属性离散化处理过程如下：

    （1）对属性的取值进行排序

    （2）两个属性取值之间的中点作为可能的分裂点，将数据集分为两部分，计算每个可能的分裂点的信息增益度（InfoGain）

    （3）选择修正后信息增益度最大的分裂点作为该熟悉的最佳分裂点

· 与离散属性不同，若当前节点划分的属性为连续属性，该属性还可以作为其后代节点的划分属性。

③。处理缺省不完整数据

· 在某些情况下，可供使用的数据可能缺少某些属性的值。例如< x , c(x) >是样本集T中的一个训练实例，但是其属性R的值R(x)未知

· 处理缺少属性值的测量包括：

    （1）忽略不完整的数据；

    （2）赋给它训练实例中该属性的最常见值；

    （3）一种更复杂的策略是为R的每个可能值赋予一个概率。

· 例如，给定一个布尔属性R，如果节点 N 包含 6 个已知 R=1 和 R=0 的实例，那么 R(x)=1 的概率是 0.6，而R(x)=0 的概率是0.4。于是，实例 x 的 60%被分配到 R=1 的分支，40%被分配到另一个分支

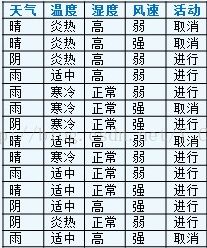
· 以下图为例，介绍用C4.5建立决策树的方法

训练集有4个属性，即属性集合 A = {天气，温度，适度，风速}；而类属性有 2 个，即类标签集合 C={ 进行，取消 }，分别表示适合户外运动和不适合户外运动

数据集 D 包含 14 个训练样本，其中属于类别“进行”的有9个，属于类别“取消”的有5个，则其信息熵为：

Info(T) = - 9/14 * log2 (9/14) -5/14 * log2 (5/14) = 0.940

对属性集中每个属性分别计算信息熵，如下所示：

Info(天气，T) = 5/14 *[-2/5 *log2 (2/5) - 3/5 *log2 (3/5) ] + 4/14 *[ -4/4 * log2 (4/4) ] + 5/14 * [ -3/5 * log2 (3/5) - 2/5 * log2 (2/5) ] = 0.694

Info(温度，T) = 4/14 * [ -2/4 *log2 (2/4) - 2/4 *log2 (2/4) ] + 6/14 * [ -4/6 *log2 (4/6) - 2/6 * log2(2/6) ] +4/14 * [-3/4 * log2(3/4) - 1/4 * log2(1/4) ] = 0.911

同理可计算 Info(湿度，T) = 0.789 ， Info(风速，T) = 0.892

信息增益率的计算：

SplitInfo（天气，T）= -5/14 *log2(5/14) - 5/14 *log2(5/14) - 4/14 *log2(4/14) = 1.577406

SplitInfo（温度，T）= -4/14 *log2(4/14) - 6/14 *log2(6/14) - 4/14 *log2(4/14) = 1.556656

同理可计算 SplitInfo（湿度，T）= 1.0 ， SplitInfo（风速，T）= 0.985

计算信息增益度：

Gain（天气，T）= Info（T）- info（天气，T）= 0.94-0.694 = 0.246

Gain（温度，T）= Info（T）- info（温度，T）= 0.94-0.911 = 0.029

同理可计算 Gain（湿度，T）=0.151，Gain（风速，T）=0.04

计算信息增益率：

GainRatio（天气，T）= Gain（天气，T）/ SplitInfo（天气，T）= 0.246 / 1.577 = 0.155952

GainRatio（温度，T）= Gain（温度，T）/ SplitInfo（温度，T）= 0.029 / 1.557 = 0.018629

同理，GainRatio（湿度，T） = 0.151，GainRatio（风速，T） = 0.04871968

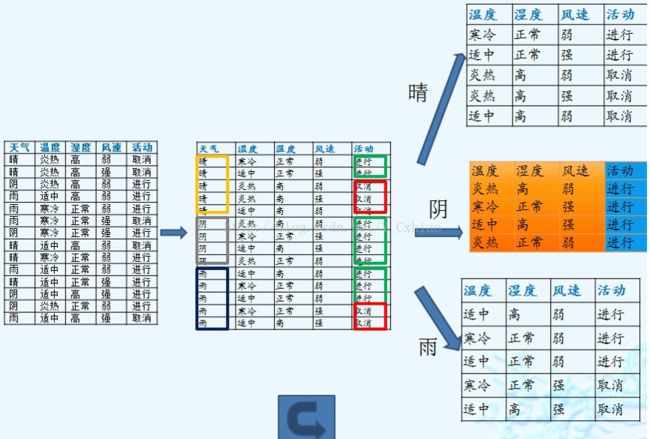
根据计算得到的信息增益率进行选择属性集中的天气属性作为决策树节点，对该节点进行分裂，如图所示：

· 目前有很多可用的C4.5软件实现，如Weka（Waikato Environment for Knowledge Analysis），是一款免费的、非商业化的、基于Java环境下开源的机器学习（Machine learning）以及数据挖掘（Data minning）软件。Weka中对C4.5的Java实现被命名为J48

④。剪枝

· 基本策略：预剪枝 、 后剪枝

预剪枝是在决策树生成过程中，如果这个节点进行划分，不能带来泛化性能的提升，则停止划分并将该节点设置为叶子节点。

后剪枝则是先训练好一棵树，然后自底向上对非叶子结点进行考察，如果该节点对应的子树替换为叶节点后能带来泛化性能的提升，则将该子树替换为叶结点。

· 预剪枝在每次决定用一个特征去划分数据集的时候，都用验证集的数据去判断这次划分能否提高验证集的精度

优点：预剪枝使得决策树很多分支都没有“展开”，这不仅降低了过拟合的风险，还显著减少了决策树的训练时间开销和测试时间开销

缺点：虽然某次划分可能并不能带来性能上的提升，但是后序的划分可能会带来性能上的提升。预剪枝给决策树带来欠拟合的风险

· 后剪枝就是从某个节点后续划分去掉，将该节点设置为叶结点时，如果性能得到提升则进行剪枝操作

从性能上来讲，后剪枝一般比预剪枝的性能要好，但是其时间开销会更大。

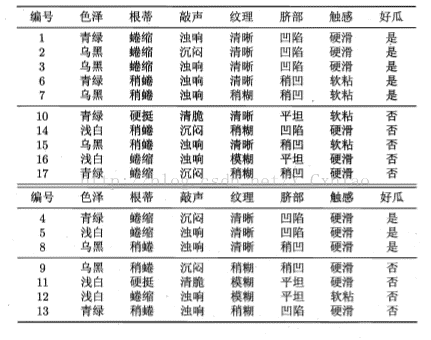
剪枝举例： （线上为训练集，线下为验证集）

未剪枝：

5. CART算法 （分类与回归树，Classification And Regression Trees）

· 采用与传统统计学完全不同的二叉树形式构建预测准则，易于理解、使用和解释。CART模型构建的预测树在很多情况下比常用的统计方法构建的代数学预测准则更加准确，且数据越复杂、变量越多，算法的优越性就越显著

· 是一种典型的二叉决策树，主要用来进行分类研究，可以同时处理连续变量和离散变量。

·  如果目标变量是离散变量，则CART生成分类决策树

· 如果目标变量是连续变量，则CART变量生成回归决策树

· CART算法与C4.5算法的相似之处：

        采用分裂准则从众多的预测属性（模型的输入属性）中确定树节点的分裂条件，把记录分到各个分支中，重复该过程建立一棵充分大的分类树，然后用简直算法对该充分大树进行剪枝，得到一系列嵌套的分类树，最后用测试数据对该一系列分类树进行测试，从中选出最优的分类树。

· CART算法与C4.5算法的不同之处：

        CART为二叉分枝，而C4.5是多叉分支

        CART的输入和输出变量可以使离散型和连续型，而C4.5的输出变量只能是离散型

        CART实用的分裂准则是Geni系数，而C4.5使用的是信息增益率

        二者对决策树的剪枝方法不同

· CART生成决策树的过程主要包括三个步骤：分裂、剪枝、树选择

（1）分裂

        分裂过程是一个二叉递归划分过程，用Y表示因变量（分类变量），用X1,X2,...Xn表示自变量，通过递归的方式把关于X的P维空间划分为不重叠的区域。首先要确定分裂准则，分裂准则的形式为：

        An instance goes left if condition ,      and goes right otherwise.

        其中condition是分裂条件表达式，对于连续属性，表达式的形式是 属性 Xi ≤ S，对于离散属性，表达式是一种列表成员的判定运算。

        与C4.5不同，CART允许在一个属性上重复分裂。

        如选择一个自变量 Xi 和 Xi 的一个值 Si，确定分裂条件，把P维空间分成两部分：一部分包含的点都满足 Xi ≤ Si，另一部分包含的点满足 Xi＞Si

        然后把上部中得到的两部分中的一个部分，通过确定分裂条件再以相似的方式划分

        重复上述步骤，直至把整个X空间划分成的每个区域都尽可能使同构的。

        · Cart算法主要使用Gini分裂准则。如果集合 T 包含 C 个类，基点 A 的Gini 系数为：

          其中，Pk 表示样本属于 k 类的概率。当 Gini=0 时节点中的所有样本属于同一类，当所有类在节点中以相同的概率出现时，Gini值最大。Gini指数最小的属性为最优划分属性

          如果集合T 在 X 的条件下划分成两个部分 T1 和T2，那么这个划分的 Gini指数为，当前属性的最优分裂点就是使 Gini(split (X) )最小的值

        · 分裂步骤为：

           1. 对于每个属性选择最优的分裂点

           2. 在这些最优分裂点中选择对这个结点最优的分裂点，成为这个节点的分裂条件

           3. 继续对此节点分裂出来的两个节点进行分裂

           4. 分裂过程一直持续到叶节点数目很少或者样本基本属于同一类别。

           · 由于CART建立二叉树，对于具有多个值的分类型属性变量，需要将多个类别合并成为两个“超类”；对于数值型属性，需要确定分裂之将样本分为两组

（2）剪枝

        CART用“成本复杂性”标准（cost-complexity pruning）来剪枝，该方法从最大树开始，每次选择训练数据集上对整体性能贡献最小的那一个（也可能是多个）分裂作为下一个剪枝的标准，如此直到只剩下根节点。这样CART就会产生一系列嵌套的剪枝树，需要从中选择一颗作为最优的决策树。

        · 树选择

              因为在树的生成过程中可能存在不能提高分类纯度的划分节点且存在过拟合训练数据的情况，这时需要使用一份单独的测试数据来评估每棵剪枝树的预测性能，从而选取最优树。

    

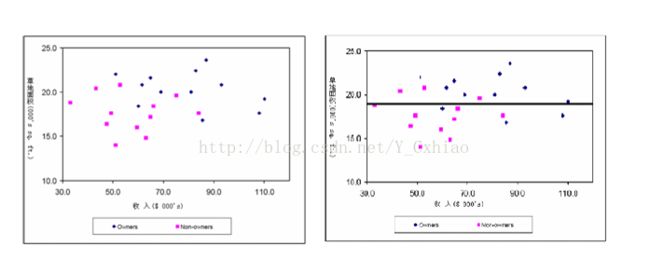
将上述表格图例化得到的结果如下图所示

根据上图可知，在使用CART算法是，首先使用 x2=19 进行分类。由图可以直观的发现两个矩形部分更加的同质（即统一类别的点更多的聚集在一起）

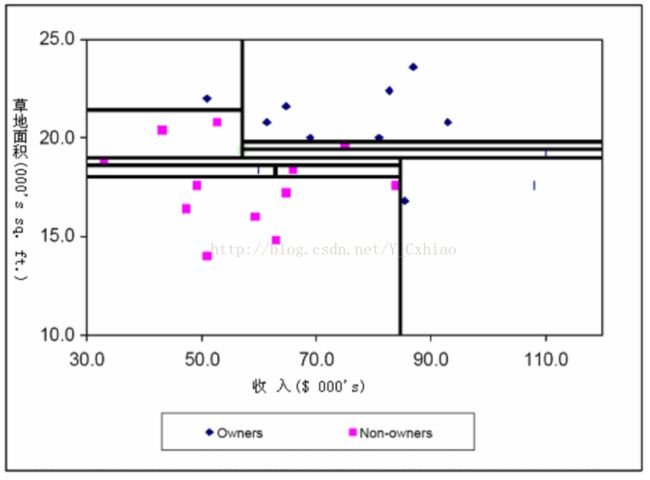
对照如上的规则对样本继续划分，经过若干次划分，可以得到下图

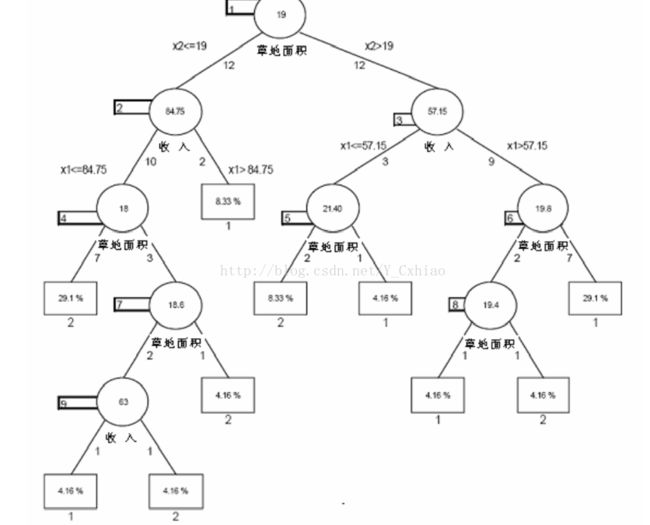
通过观察得知，每一个矩形都是同质的，即质保函一种类别的点。该算法每一次划分都将节点划分为两个子节点，最终形成下图所示的树形结构

简化的树生长算法如下：

    开始：将所有数据分配给根节点并将根节点定义为叶结点

    分裂：

        New_split = 0

        for(树中的每个叶节点）

            if（ 叶节点的样本数量太少或者节点中的所有点属于同一个类）

                  goto GetNext

                  根据分裂准则找的最优分类属性和阈值，将节点分裂成两个新的子节点

                   New_split++;

                   GetNext;

简化的剪枝算法如下所示：

        定义：

            r(t) = 节点 t 中，训练数据被误分的比例

            p(t) = 节点 t中，包含的训练实例数目

            R(t) = r(t) * p(t)

            t_left = 节点 t 的左子树

            t_right = 节点 t 的右子树

            |T| = 树 T 中叶结点的总数

        开始：

            Tmax = 最大生长树

            Current_tree = Tmax

            for（所有叶结点的父节点 t）

                将所有的 R(t) = R(t_left) +  R(t_right）的分裂点移除

            Current_tree = 剪枝后的Tmax

        剪枝：

            if（|Current(tree)|） = 1

                  goto DONE

            for（所有节点的父节点 t）

               将 R(t) - R(t_left) - R(t_right)最小的那个点移除

            Current_tree = 剪枝后的Current_tree

        因为树不需要调整参数，CART要求开发者付出相对小的努力。不需要对变量进行转换。该算法可以生成简单易懂的规则，可以处理连续和多种类字段，并且可以清楚的显示哪些字段比较重要。但是该算法也有相应的缺点，CART是一种大样本的统计分析方法，样本量小时构建的模型并不稳定。选择划分时依靠观测点的值得顺序而不是按照这些值的绝对大小；对连续性的字段比较难预测。对于有时间顺序的数据，需要很多预处理的工作。当类别太多时，错误可能就会增加的比较快。

        Weka中提供了CART算法的基本实现：weka.classifiers.trees.SimpleCart

6.SVM算法（Support Vector Machine，支持向量机）

    · 在解决小样本、非线性及高维模式识别中表现出特有的优势，并能够推广应用到函数拟合等其他机器学习问题中。

    · 目前，该死心已经成为最主要的模式识别方法之一，使用支持向量机可以在高维空间中构造良好的预测模型。

（1）线性可分SVM

    · 支持向量机来源于最为基本的线性分类器。线性分类器通过一个超平面将数据分成两个类别，该超平面上的点满足：

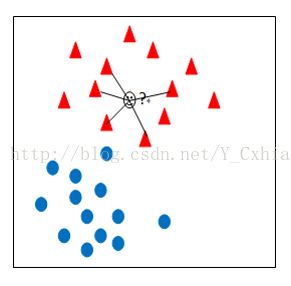
    · SVM采用了这种方式，将分类问题简化为确定的符号，大于0为一类，小于0为 另一类，如何寻找这样的一个最优的超平面是SVM要解决的基本问题。下面通过一个例子来解释SVM中超平面的概念。

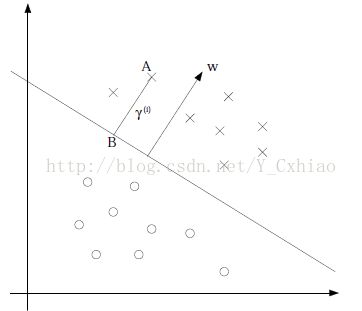
如上图，对于点ABC来说，可以认为将A并入 “X” 这一类的置信度是很高的，对于B来说，置信度就没有A高，但是总体来说是可信的。但是对于C来讲，就很难说是否应该并入 “X” 这一类。因此，找到一个能够让两类数据都离超平面很远的超平面，就是支持向量最基本的任务。在SVM中，使用几个间隔来确定距离。

如上图，给出了超平面（ω，b）和其法向量ω。点A表示某一实例 Xi ，其类标记为 Yi=±1 。点A与超平面（ω，B）的距离线段由线段AB给出，记作γi，则

其中，||ω|| 为ω的L2范数。这是点A相对于超平面为“+1”的计算公式。如果点A在相对于超平面类别为“-1”的一侧，那么点A与超平面的距离为

那么根据上面得出的两个公式，可以计算得出当一个点被正确的分到一侧时候，该店与超平面的距离为

定义超平面（ω，b）关于训练数据集T的几何间隔为超平面关于T中所有样本点的几何间隔最小值，即

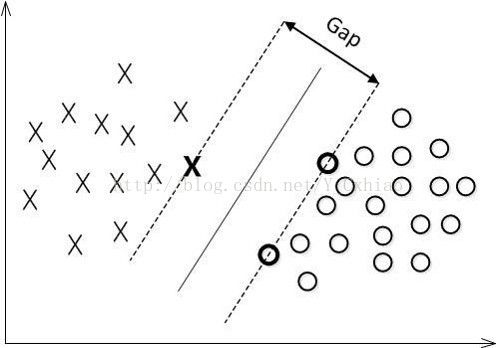
如下图就是一个线性可分的SVM的优化目标示意图。优化的目标就是让图中的“Gap”尽量的大

于是最大间隔分类器的目标函数可以定义为

显然，几何间隔必须满足自身的定义，也就是取所有样本的几何间隔的最小值，这样，这个优化问题就变成了带约束的优化问题，优化的约束条件为

可以把上述约束型优化进行变形，即 

变形后的约束型优化目标函数可以简化有画的计算，经过简化，线性可分SVM的最终约束型优化问题就可以写为

（2）线性不可分SVM 

 ①对偶算法

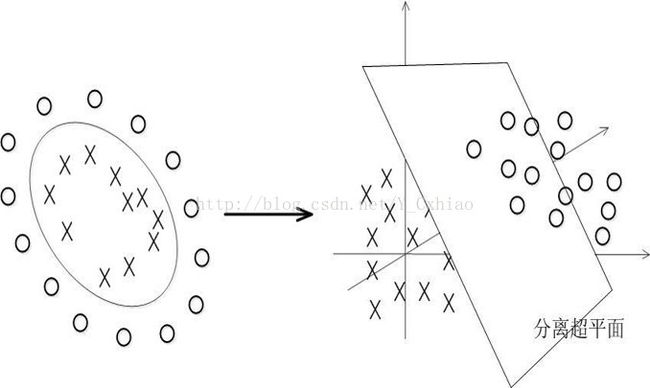
        SVM使用对偶算法求解最优化的问题。通过给每一个约束条件加上一个拉格朗日乘子，定义拉格朗日函数，然后使用拉格朗日函数进一步简化目标函数，从而只用一个函数表达式便能清楚的表达出问题

        其中，为拉格朗日乘子向量

        那么根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题

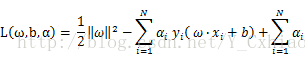
        也就是说，可以通过引入拉格朗日乘子，原始问题变成了一个先求 L(ω，b，a)对ω，b的极小，再求对a的极大

        第一步就是求极小，使用数学中求极小的方法，需要先对拉格朗日函数函数L(ω，b，a)分别求偏导数并令其等于0，那么就可以得到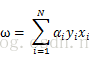  

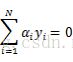
        将上述结果带入拉格朗日函数，就可得到极小值，即

        接下来，就可以对上式进行极大值的求解，如果把上式的负号改变，也就是取，那么极大问题就转换成求变换符号后的极小问题，这样做的目的是为了与上文中线性可分SVM的目标函数一致，也就是   、  、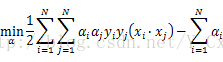    

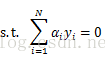        利用拉格朗日对偶性的另一个目的是引入非线性分类的方式，也就是非线性SVM的核心问题“核函数”

  ②核函数

如上图所示就是一个典型的非线性的例子。从图中可以看到，对于红色和紫色两种不同的类别，任何一个超平面都不能将其完整的分开，必然存在大量错误分类的情况。针对这种情况，SVM引入了核函数，解决了非线性的问题。

        SVM的判别函数是，将对偶问题中求得的带入其中，可以得到对偶问题中的判别函数的表达形式为

        这里的形式的有趣之处在于，对于新点X的预测，只需要计算它与训练数据点的内积即可，这一点至关重要，是核函数使用的基础。

        计算内积是处理线性不可分的一种常用的方式。也就是将处在低维的线性不可分的数据，通过映射的方式，投影到高位的空间中，使这些数据变成线性可分的数据，这样就可以使用线性可分SVM进行分类。不妨假设这种映射关系为。那么根据上文中提到的内积计算方式，可以得到映射之后的最优化目标函数为：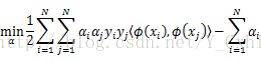

如此，通过一个低维到高维的映射，就可以把线性不可分的问题解决了。但事实上，这种方式有很大的运算负担。因此，需要一种能够不进行低维到高维的映射，直接可以在现有维度进行计算的方式来解决线性不可分的问题。这样的一种方法，就是所谓的“核函数”

        设 X 是输入空间，又设ψ为特征空间，如果存在一个从X到ψ的映射，使得所有的 ，函数K(x,z) 满足条件 ，则称为核函数，其中，φ(x)·φ(z)为两者的内积

        核函数的核心思想是，在分类与预测中只使用核函数K(x,z)，而不需要关心映射函数和映射空间。再引入核函数之后，SVM的目标函数就可以改写为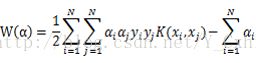

        决策函数也可以使用核函数进行计算，使用核函数的决策函数为

        以上就是SVM利用核函数解决线性不可分问题的方法，从线性可分到线性不可分，SVM的基本思想没有变，还是寻找最优的超平面，只是在非线性的时候，还需要通过核函数来求解。

常用的核函数：

  ③松弛变量

        松弛变量的引入是为了解决噪音点的问题。对于这种偏离正常位置很远的数据点，称之为outlier。在SVM中，如果数据存在噪声点，并且这些噪声点离超平面很近的话，会对SVM的分类结果造成非常大的影响

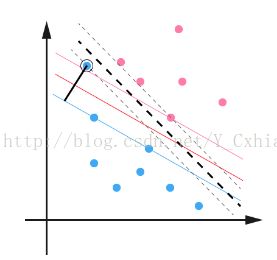
    如上图，用黑圈圈起来的蓝点就是一个outlier，由于这个outlier的出现，导致分隔超平面不得不被挤压歪了，变成图中黑色虚线所示。

    为了处理这种情况，SVM允许数据点在一定程度上偏离超平面。如上图中，黑色实线所对应的距离，就是该outlier偏离的距离，如果把它移动回来，就刚好落在了原来的超平面上，就不会使得超平面发生变形了。这个偏移的距离就是松弛变量。

    不妨设松弛变量为，那么约束优化的条件就变成了

    而如果不对松弛变量进行限制，而让其任意大的话，上述约束条件也就失去了意义。因此，对于松弛变量，要使其总和最小，也就是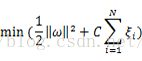

    其中C是一个参数，用于控制目标函数中两项“寻找几何间隔最大的超平面”和“保证数据点偏差量最小”之间的权重，这个参数也被称作为“惩罚参数”。那么，对于上面得到的加入松弛变量的目标函数进行拉格朗日对偶变形，可以得到加入松弛变量后的约束型优化问题的公式：

可以发现，引入了松弛变量之后的SVM仅仅是让拉格朗日乘子多了一个限制条件C。而这样的一个SVM就可以有效的对抗噪声点的干扰

（3）参数设置

①优化方法

    上文已经介绍了SVM的基本概念，而在实际操作中，需要针对不同的数据集进行相关参数的调解。在SVM中，需要调节的参数包括上文中提到的 “惩罚参数”C，以及”核函数参数“g。通常的方式是采用”交叉验证“（Cross-validation）或者简称CV的方法来优化参数。采用CV的思想可以在一定程度上得到最优的参数，可以有效避免过学习和欠学习状态的发生，最终对于测试集合的预测得到较理想的准确率

②参数优化实例

    Wine数据集记录的是意大利同一区域里三种不同品种的葡萄酒的化学成分分析，数据里有179个样本，每个样本包含13个特征分量。http://archive.ics.uci.edu/ml/

    注意：当有多组c和g都对应较高的分类准确率的时候，应当选择c最小的一组参数最为c和g最佳的参数。因为过高的c会导致过学习状态发生，即训练集分类准确率很高而测试集分类准确度很低（过拟合，分类器的泛化能力降低）

（4）SVM算法的软件实现

    Weka本身没有提供SVM的程序包，可以使用LIBSVM软件包，由台湾大学开发的一个快速有效的SVM模式识别的软件包。需要先把SVM下载下来，然后再指定好libsvm.jar的路径，weka就可以正常的使用了

    实验步骤如下：

1）下载LibSVM.http://www.csie.ntu.edu.tw/~cjlin/libsvm/. 下载页面上提供的.zip压缩包，解压缩到指定目录。

2）设定libsvm.jar到CLASSPATH。即在CLASSPATH中添加libsvm.jar所在的路径。把libsvm.jar文件放到weka的安装目录下。然后打开runweka.ini这个文件，把cmd_default=javaw -Xmx#maxheap# -classpath"%#此前在首页部分显示#CLASSPATH%;#wekajar#"#mainclass# 修改为cmd_default=javaw -Xmx#maxheap# -classpath"%CLASSPATH%;#wekajar#;libsvm.jar" #mainclass#然后直接运行runweka.bat，打开Explorer，可以在Classify的Classifier-function中找到LibSVM，像使用其它Classifier一样使用它就可以了。

3）打开breast-cancer.arff文件，切换到classify面板。

4）选择functions——>libSVM分类器。

5）Testoptions选择默认的十折交叉验证。

6）点击start按钮，启动实验。

7）在右侧的Classifieroutput分析实验的结果。

    分类结果：

再通过Wine数据集对核函数的使用效果进行测试

        在这178个样本中，第1~59个样本属于第一类（类别标签为1），第60~130个属于第二类（类别标签为2），第131~178个属于第三类（类别标签为3）。实例中将每个类别分成两组，重新组合数据，一部分作为训练集，一部分作为测试集。

        下图就是使用SVM进行分类后的结果图。可以发现，SVM将三种葡萄酒进行了分类，分类的准确率很高，只有第二个类别中有一个被错误的分到第三个类别中。因此，可以说明SVM在实际应用中是可以很好的完成分类任务的

        对于这个实例可以进行一下扩展。核函数的种类有很多，最为常用的是高斯核函数。高斯核函数可以应用的范围很广，一般都采用高斯核进行运算。不过，有时候其它种类的核函数也能够达到高斯核的效果，那么不妨在这个实例中测试一下几个最常用的核函数的分类效果。

        除了上文中提到的高斯核，再使用线性核函数，多项式核函数，以及sigmoid核函数进行分类测试。在使用不同的核函数的时候，测试集和训练集都是一样的，参数也是一样的，这样保证最终的分类准确率只是受核函数的影响。那么最终的分类结果如下所示：

        可以发现，采用多项式核与采用高斯核得到的结果是一样的，也就是对于wine数据集，这两种核函数都是可行的。而sigmoid核函数的准确率很低，很明显不适合这个数据集。因此，在SVM的实际中应用中核函数的选择非常重要，错误的核函数会让分类的效果非常不好。

7. KNN算法（K-Nearest Neighbor，k最邻近算法）

        决策树分类框架包含两个部分，第一步是归纳，由训练数据构建分类模型，第二部是演绎，将构建的分类模型应用于测试样本。决策树的学习方法数据 积极的学习方法（eager learnner），即先对训练数据进行学习，得到分类模型，然后对未知数据分类。与之相反的学习策略为 消极学习方法（lazy learnner），即推迟对训练数据的建模，直到需要对未知样本进行分类时才进行建模。

        

        KNN算法是一种典型的消极学习器，其基本思想是：如果一个样本在特征空间中的k个最相似（即特征空间中最临近）的样本中的大多数属于某一个类别，则该样本也属于这个类别，其中所选择的邻居样本是类别已知的训练样本。

        KNN算法不仅可以用于分类，还可以用于回归。通过找出一个样本的k个最近邻居，将这些邻居的平均值赋给该样本，就可以得到该样本的属性。更准确的方法是将不同距离的邻居对该样本产生的影响赋予不同的权值（Weight）

        如图所示，每张照片在平面上的位置用(x，y)来代表，x轴代表照片中头发的长度，y轴代表照片中脸面积的大小，用三角形代表女生的大头照，圆形代表男生的大头照。现在有一些标记已知的照片，当需要识别一张新的大头照（用打问号没有颜色的点代表)的类别时，首先设定k（最近邻邻居的数目）的值。如果K设定成1，代表会从已标记的照片中找离新的大头照最近的照片，然后看这张照片是男生(圆形)还是女生(三角形)。如果这个点是男生，那么预测新的大头照是男生的大头照。如果k=3，先计算图中打问号的点和各个有颜色点的距离，接着选出前三名距离最近的点，然后使用“多数同意规则”（majorityvoting rules），看看里面三角形的点比较多(2个以上的点是三角形)还是圆形的点比较多(2个以上的点是圆形)，如果圆形点比较多，就判断这个新问号点是男生的大头照了。

① 算法描述

    基本的KNN算法如下：

    输入： 训练集 D，测试对象 z，对象的类标签集合 L，最近邻居数目 K

    输出：Cz，即z的列别

    foreach y 属于D

    do

        计算d（y，z），即y和z的距离

    end

    从数据集D中选出子集N，N包括k个距离z最近的训练对象。

    其中，I()是一个指标函数，当其值为true时返回1，否则返回0

    算法步骤：

    （1）初始化距离为最大值

    （2）计算未知样本和每个训练样本的距离dist

    （3）得到目前k个最邻近样本的最大距离MaxDist

    （4）如果dist小于MaxDist，则将该训练样本作为k-最邻近样本

    （5）重复步骤234，直到未知样本和所有训练样本的距离都算完

    （6）统计k个最邻近样本中每个类别出现的次数

    （7）选择出现频率最大的类别作为未知样本的类别

    注意要点：

    （1）KNN算法中k值选择对算法的性能影响很大，如果k太小，则最近邻分类器容易受到由于训练数据中的噪声而产生的过拟合的影响；如果k太大，最近邻分类器可能会误分测试样例，因为最近邻可能包含远离其近邻的数据点。一般采用先定一个初始值，然后根据试验测试的结果调整k值

    （2）当样本不平衡时，即一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的k个邻居中大容量类的样本占多数。样本不平衡的问题可以采用权值的方法来改进。和该样本距离小的邻居权值大，和该样本距离大的邻居权值则相对较小。将距离远近的因素考虑在内，避免样本不平衡导致误判的情况

    算法缺陷：

    需要存储全部的训练样本

    需要进行繁重的距离计算

②改进算法

（1）分组快速搜索近邻法

   分组快速搜索近邻法时KNN算法的改进，将样本集按近邻关系分解成组，给出每组质心的位置，以质心作为带标点，和未知样本计算距离，选出距离最近的一组或若干组，再在组的范围内应用一般的knn算法。由于并不是将未知样本与所有样本计算距离，故该改进算法可以减少计算量，但并不能减少存储量

（2）压缩近邻算法

    压缩近邻算法利用现在的样本集，采取一定的算法产生一个新的样本集，该样本集拥有比原样本集少很多的样本数量，但仍然保持有对未知样本进行分类的能力

    其基本思路时定义两个存储器，一个用来存放生成的样本集，称为output样本集；另一个用来存放原来的样本集，称为original样本集。首先初始化，即output为空集，元样本集存入original。从original样本集中任意选择一个样本移动到output样本集中；然后再original样本集中选择第 i 个样本，并使用output样本集中的样本对其进行最近邻算法分类，若分类错误，则将该样本移动到output样本集中，若分类正确，不做任何处理。重复以上步骤，直至遍历完original样本集中的所有样本。

    通过这种方式也能减少算法的计算量，但仍然无法减少存储量

③ KNN分类器的特点

（1）是一种基于实例的消极的学习方法，虽然不需要建立分类模型，但是分类测试样例的开销很大

（2）基于局部信息进行学习，对噪声敏感

（3）与决策树的直线决策边界相比，knn可以生成任意形状和决策边界

④ 算法实现

    以Weka中的KNN算法实现对iris数据的分类。实验数据来源于iris。该数据以鸢尾花的特征作为数据来源，数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性，是在数据挖掘常用的测试集、训练集。数据分为三类，分别是setosa，versicolor和virginica。数据包含4个独立的属性，这些属性变量测量植物的花朵，例如萼片和花瓣的长度等。

具体的实验步骤如下：

•1）打开iris.arff文件，切换到classify面板。

•2）选择Lazy->IBk分类器，单击，设置k值为3，即参考的邻居的数目。

•3）Testoptions选择默认的十折交叉验证，点开More options，勾选Output predictions。

•4）点击start按钮，启动实验。

•5）在右侧的Classifieroutput分析实验的结果。

•6）可以多次设置K值，得到不同K值下的准确率，会发现改变K值对分类结果的影响比较复杂。

8. Naive Bayer（朴素贝叶斯分类器，又称 NBC）

    发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率

①基础知识

（1）条件概率：事件A在另一个事件B已经发生的条件下发生的概率，称作在B条件下A的概率，表示为

（2）联合概率：表示两个事件共同发生的概率

（3）贝叶斯定理：用来描述两个条件概率之间的关系，例如P(A|B) 和P(B|A)。按照乘法法则，P(A∩B)=P(A)*P(B|A)=P(B)*P(A|B)，可以导出贝叶斯定理公式：

P(A|B) = P(B|A) * P(A) / P(B)

（4）全概率公式：

②算法描述

    朴素贝叶斯的基本思想是对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，分类出概率最大的，就认为此待分类项属于该类别

（1）每个数据样本用一个n为特征向量 X={x1,x2,...,xn} 表示，描述由属性A1,A2,...,An对样本的n个度量

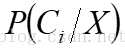（2）假定有m个类C1,C2,...,Cm。给定一个未知的样本数据X（即没有类标号），分类法将预测X属于具有最高后验概率（条件X下）的类。也就是说，朴素贝叶斯分类将未知的样本分配给类Ci，当且仅当。这样，最大化，其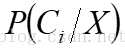值最大的类为最大后验假定。根据贝叶斯定理有，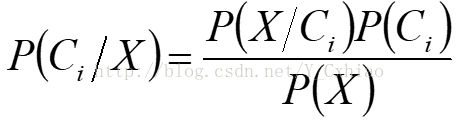

（3）由于P(X)对于所有类为常数，只需要最大即可。如果这些类是等概率的，即P(C1)=P(C2)=...=P(Cm)，据此只需要最大化。否则，最大化。其中类的先验概率可以用P(Ci)=Si/S计算，其中si是类别Ci的训练样本树，而s是训练样本总数。

（4）给定具有许多属性的属性集，计算P(X/Ci)的开销可能非常大。为了降低计算开心，可以做类条件独立的朴素假定。即朴素的贝叶斯方法假设对于每个类别，属性间相互条件独立，即在属性间，不存在依赖关系。在该假设条件下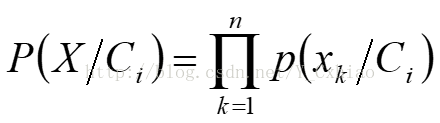，，概率P(X1|Ci),P(X2|Ci),...,P(Xn|Ci)可以由训练样本估值。其中

      （a）如果Ak是分类属性，则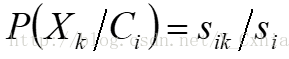，其中Sik是在属性Ak上具有值Xk的属于类Ci的样本数，而Si是Ci中的训练样本数。

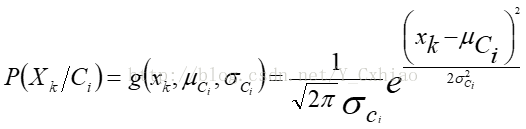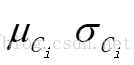      （b）如果Ak是连续值属性，则通常假定该属性服从高斯分布，因而。其中，给定类Ci的训练样本属性Ak的值，是属性Ak的高斯密度函数，而分别为平均值和标准差

（5）对未知样本X分类，对每个类Ci，计算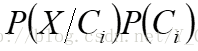，样本X被指派到类Ci，当且仅当。换言之，X被指派到其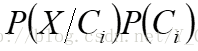最大的类Ci。

③算法评价

    理论上讲，与其他所有分类算法相比较，贝叶斯分类具有最小的出错率。然而，实践中并非总是如此。这是由于对其应用的假定（如类条件独立性）的不准确性，以及缺乏可用的概率数据造成的。然而种种实验研究表明，与判定树和神经网络分类算法相比，在某些领域，该算法确实可以与之媲美。

    当某个类别下某个特征项划分没有出现时，就会产生P(X|C)=0这种现象，这会令分类器质量大大降低。为了解决这个问题，引入了Laplace校准，他的思想非常简答，就是对每个类别下所有划分的计数+1，这样如果训练样本集数量充分大时，并不会对结果产生影响，并且解决了上述频率为0的尴尬局面

④贝叶斯分类模型的特点

· 训练过程非常简单，对海量数据的训练集表现非常高效

· 面对孤立的噪声点，具有较强的健壮性

· 模型的可读性也比较强，对于分类得到的结果可以进行解释

· 在现实世界中，特征属性之间往往是不独立的，所以对相关性很强的数据集使用此模型得到的分类结果会比较差

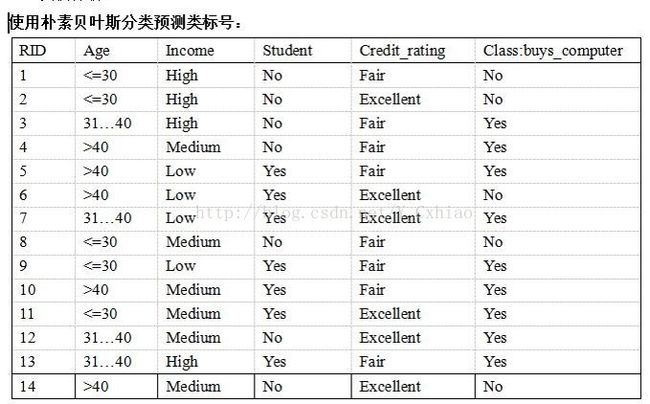
⑤实例分析

数据样本用属性age，income，student和credit_rating描述。类标号属性buys_computer具有两个不同值（即（yes，no））。设C1对应于类buys_computer=“yes”，而C2对应于类buys_computer=“no”。待分类的样本为

需要最大化，i = 1,2

每个类的先验概率P(Ci)可以根据训练样本计算：

P(Buys_computer="Yes") = 9/14 = 0.643

P(Buys_computer="No") = 5/14 = 0.357

计算下面的条件概率：

P(Age="<30"|buy="yes") = 2/9 =0.222

P(Age="<30"|buy="no") = 3/5 = 0.222

P(income=”medium”|buys_computer=”yes”)=4/9=0.444

P(income=”medium”|buys_computer=”no”)=2/5=0.400

P(student=”yes”|buys_computer=”yes”)=6/9=0.667

P(student=”yes”|buys_computer=”no”)=1/5=0.200

P(credit_rating=”fair”|buys_computer=”yes”)=6/9=0.667

P(credit_rating=”fair”|buys_computer=”no”)=2/5=0.400

使用以上概率，得到

P(X|buys_computer=”yes”)=0.222×0.444×0.667×0.667=0.044

P(X|buys_computer=”no”)=0.600×0.400×0.200×0.400=0.019

P(X|buys_computer=”yes”)P(buys_computer=”yes”)=0.044×0.643=0.028

P(X|buys_computer=”no”)P(buys_computer=”no”)=0.019×0.357=0.007

因为P(X|buys_computer=”yes”)P(buys_computer=”yes”)大于P(X|buys_computer=”no”)P(buys_computer=”no”)，所以对于样本X，朴素贝叶斯分类预测uys_computer=”yes”。

⑥软件实现

•在weka软件中NaiveBayes算法实现了朴素贝叶斯分类器的算法。使用天气数据集对贝叶斯分类器进行训练并评估分类模型的性能。

具体的实验步骤如下：

•1）打开weka自带的weather.numeric.arff文件，切换到classify面板。

•2）选择bayes>NaiveBayes分类器。

•3）Testoptions选择默认的十折交叉验证

•4）点击start按钮，启动实验。

•5）在右侧的Classifieroutput分析实验的结果。

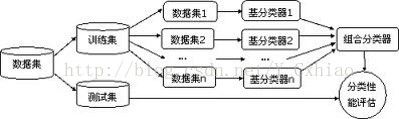
9.集成学习（Ensemble learning，又称组合学习）

    通过聚集多个分类器的预测来提高分类准确率。集成学习由训练数据构建一组基分类器（Base classifier），然后通过每个基分类器的预测的投票来进行分类。由于训练样本的可变性是分类器误差的主要来源，通过聚集在不同的训练集上构建的基分类器有助于减少这种类型的误差。

    集成方法对于不稳定的分类器的提升效果较好，不稳定的分类器是指对训练集微小变化敏感的分类器，包括决策树、基于规则的分类器和人工神经网络等。

① 集成分类器的构造——袋装（bagging）

    袋装是一种根据均匀概率分布从数据集中重复抽样（有放回）的技术。每个样本集和原始数据一样大。由于抽样过程是有放回的，因此一些样本可能在同一个训练集中出现多次，而另一些可能被忽略。该方法的主要过程如下：

（1）重复的从一个样本集合D中进行n次有放回的随机抽样，得到一个子样本集

（2）对每个子样本集，进行统计学习，获得假设Hi

（3）将若干个假设进行组合，生成最终的假设Hfinal

（4）将最终的假设用于具体的分类任务

②分类器的构造——提升（（Boosting）

     提升是一个迭代过程，用来自适应的改变训练样本的分布，使基分类器聚焦在那些被错分的样本上。提升给每一个训练样本赋一个权值，在每一轮提升过程结束时自动的调整权值。训练样本的权值主要作用于以下两个方面：

（1）用作抽样分布，从原始数据集中抽取样本集

（2）基分类器使用权值，学习偏向于高权值样本的模型

    限制已经有很多种提升算法的实现，这些算法的主要差别在于更新样本权重的算法和如何汇集各个分类器的预测。

Adaboost算法

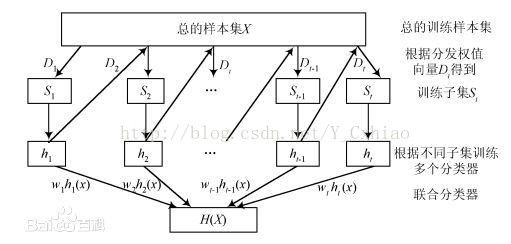
    Adaboost是机器学习中一种比较重要的迭代算法，其核心思想是针对同一个训练集训练不同的分类器（弱分类器），然后把这些弱分类器集成起来，构成一个更强的最终分类器（强分类器）。其算法本身是通过改变数据分布来实现的，它根据每次训练集中每个样本的分类是否正确，以及上次的总体分类的准确率，来确定每个样本的权值。将修改过权值的新数据集送给下层分类器进行训练，最后将每次训练得到的分类器集成起来，作为最后的决策分类器。

    Adaboost是使用最为广泛的提升方法，主要框架描述如下：

③Bagging 和 Adaboost 的不同

    和袋装不同，在Adaboost中每次迭代改变的是样本的分布，而不是重复采样。样本分布的改变取决于样本是否被正确分类。分类正确的样本权值低，分类错误的样本权值高。汇集各个分类器的预测没有采用多数表决的方案，最终的结果是弱分类器的加权组合。权值表示该弱分类器的性能。

    Bagging中各个训练集是独立的，而Adaboost中的训练集依赖于上一个训练集，Bagging的每个弱分类器的组合权重是相等的，而Adaboost中每个弱分类器组合起来的权重不一样

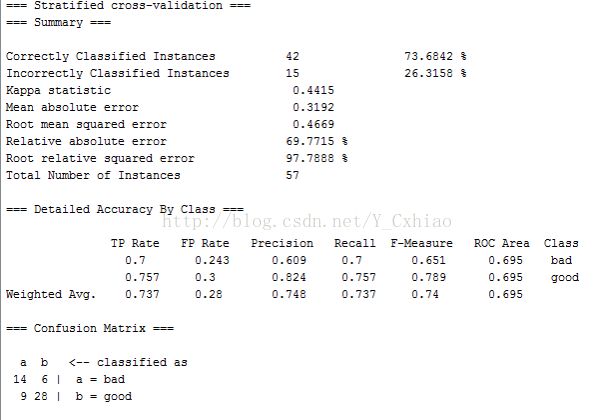
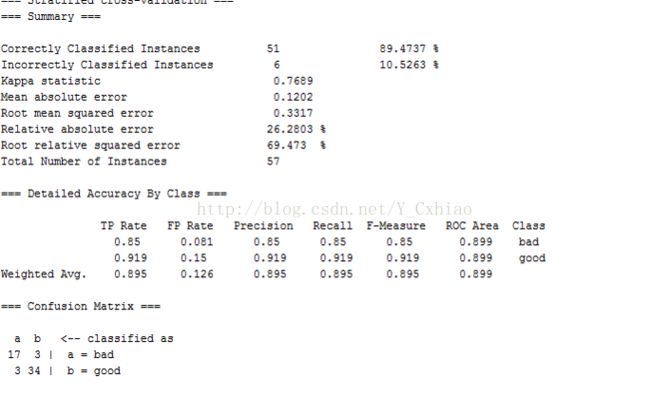
④Adaboost算法实验

•（1）对labor数据采用J48分类结果如下图

•（2）采用adaboost

         1）打开labor.arff文件，切换到classify面板。

        2）选择meta->adaboostM1分类器，单击，设置classifier值为J48

         3）点击start按钮，启动实验。

•（3）实验结果下图所示

•通过两个实验结果对比发现adaboost算法将J48分类器的分类结果提高了16%左右。

10. 分类算法及评估指标

①分类评价中的常用术语如下表所示

（1）True positives(TP):  被正确地划分为正例的个数，即实际为正例且被分类器划分为正例的实例数（样本数）；

（2）False positives(FP): 被错误地划分为正例的个数，即实际为负例但被分类器划分为正例的实例数；

（3）False negatives(FN):被错误地划分为负例的个数，即实际为正例但被分类器划分为负例的实例数；

（4）True negatives(TN): 被正确地划分为负例的个数，即实际为负例且被分类器划分为负例的实例数。

（5）混淆矩阵（confusion matrix）是用来反映某一个分类模型的分类结果，其中行代表的是真实的类别，列代表的是模型预测的类别。

②分类算法的评价指标包括

（1）正确率（accuracy）。accuracy= （TP+TN）/(P+N)，即被分对的样本数除以所有的样本数，正确率越高，分类器越好；

（2）错误率（error rate)。错误率则与正确率相反，描述被分类器错分的比例，error rate = (FP+FN)/(P+N)，对某一个实例来说，分对与分错是互斥事件，所以accuracy =1 -  error rate。

（3）灵敏度（sensitive）。sensitive= TP/P，表示的是所有正例中被分对的比例，衡量了分类器对正例的识别能力；

（4）特效度（specificity)。specificity= TN/N，表示的是所有负例中被分对的比例，衡量了分类器对负例的识别能力；

（5）精度（precision）。精度是精确性的度量，表示被分为正例的实例中实际为正例的比例，precision=TP/（TP+FP）；

（6）召回率（recall）。召回率是对覆盖面的度量，度量有多个正例被分为正例，recall=TP/(TP+FN)=TP/P=sensitive，可以看到召回率与灵敏度是一样的。

（7）其他评价指标。ROC曲线和AUC（曲线包围面积）。ROC（ Receiver Operating Characteristic）接收者操作特征曲线，又被称为ROC曲线，来源于信号检测领域，可用于比较两个分类器的性能。ROC曲线关注两个指标TPR （true positive rate ）和FPR（falsepositive rate）。

TPR =TP /（TP +FN ）

FPR =FP /（FP +TN ）

直观上，TPR代表能将正例分对的概率，FPR代表将负例错分为正例的概率。在ROC 空间中，每个点的横坐标是FPR，纵坐标是TPR，这也就描绘了分类混淆矩阵中FP-TP两个量之间的相对变化情况，反映了FP与TP之间权衡。

对于二值分类问题，二元分类器输出的是对正样本的一个分类概率值，通过设定一个阈值可以将实例分类到正类或者负类（例如大于阈值划分为正类）

如果阈值发生变化，就需要用不同的阈值进行分类，根据分类结果计算得到ROC空间中相应的点，连接这些点称为ROC曲线

ROC曲线经过(0,0),(1,1)。一般情况下，这个曲线都应该处于（0,0）和（1,1）两点连线的上方。

AUC的值就是处于ROC curve下方的那部分面积的大小，用来衡量分类器的好坏。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的分类器性能。

在TPR随着FPR递增的情况下，TPR增长的越快，曲线越往上凸，AUC就越大，模型的分类性能就越好。当正负样本不平衡时，这种模型评价方式比一般的精确度评价方式有明显的优势

分类模型的误差包括训练误差和泛化误差两种。

训练误差是在训练集中错误分类样本的比率，泛化误差是模型在未知记录上的期望误差，训练数据中推导出的模型能够适用于新数据的能力

一个好的分类模型应该具有低的训练误差和泛化误差，评估分类模型的性能主要是估计其泛化误差。

（分类模型只要足够复杂，是可以完美地适应训练数据的，但当运用于新数据时会导致较高的泛化误差即模型过度拟合问题。如对于决策树模型，随着树中节点的增加，起初模型的训练误差和泛化误差会不断降低，但是当树的节点增加到一定规模，树模型越来越复杂时，其训练误差不断降低，但泛化误差开始增大，出现过度拟合。）

常见交叉验证的方法包括：

1.Hold-Out Method。将原始数据随机分为两组，一组做为训练集，一组做为验证集，利用训练集训练分类器，然后利用验证集验证模型，记录最后的分类准确率。

2.K-fold Cross Validation。将原始数据分成K组(一般是均分)，将每个子集数据分别做一次验证集，其余的K-1组子集数据作为训练集，这样会得到K个模型，用这K个模型最终的验证集的分类准确率的平均数作为此分类器的性能指标。K一般大于等于2，实际操作时一般取10。

3.Leave-One-Out Cross Validation。如果设原始数据有N个样本，每个样本单独作为验证集，其余的N-1个样本作为训练集，得到N个模型，用这N个模型最终的验证集的分类准确率的平均数作为分类器的性能指标。相比于K-fold Cross Validation，Leave-One-OutCross Validation有两个明显的优点:①.每一回合中几乎所有的样本皆用于训练模型，因此最接近原始样本的分布，这样评估所得的结果比较可靠。②.实验过程中没有随机因素会影响实验数据，确保实验过程是可以被复制的，其缺点是计算成本高。

③调参

•大多数学习算法都有些参数需要设定，参数配置不同，学得模型的性能往往有显著差异。而由于参数一般为实数取值，所以并不能把各个参数都试一遍，然后再比较。

•现实中常用的做法是对每个参数选定一个范围和变化步长。

•例如参数范围为[0,0.2],选择步长为0.05,则评估候选参数有5个。