从零点五开始的深度学习笔记——VAE(Variational AutoEncoder) (一) 预备知识
VAE-Variational AutoEncoder 学习笔记
- 1. VAE变分自动编码器
-
- 1.1 Stacked AutoEncoder 回顾
- 1.2 Variational AutoEncoder 结构
- 2. 预备知识
-
- 2.1 概率
-
- 2.1.1 概率分布
- 2.1.2 条件概率
- 2.1.3 贝叶斯定理 (Baye's theorem)
- 2.1.4 全概率定理(Theorem of total probability)
- 2.2 矩阵迹计算技巧
- 2.3 KL散度 (Kullback-Leibler Divergence)
-
- 2.3.1 介绍
- 2.3.2 KL散度的属性(properties):
- 2.3.3 多变量正态分布之间的KL散度计算
- 3. 总结
1. VAE变分自动编码器
变分自动编码器是生成模型(generative model)中常见的系列之一,常见的生成模型还有GAN。这篇博文主要参考了 Ahlad Kumar视频中对VAE核心公式的解释和推导,力图将完整的实现和推导过程整理成笔记。这篇笔记所整理的内容是2019年1月11日的一个Ahlad Kumar博主的VAE系列视频教程,除此之外还加入了一些个人的理解。我们将逐渐过渡到cVAE (conditional Variational AutoEncoder)。
视频参考链接:https://www.youtube.com/watch?v=w8F7_rQZxXk
1.1 Stacked AutoEncoder 回顾
下面的图片展示了Stacked AutoEncoder的结构图(来源为lilianweng github账号中的一张图片),主要包括一个编码器,一个bottleneck和一个解码器,任务目标是重建图像(看图中的Cost function),最终得到一个bottleneck,作为图像的低维表示。

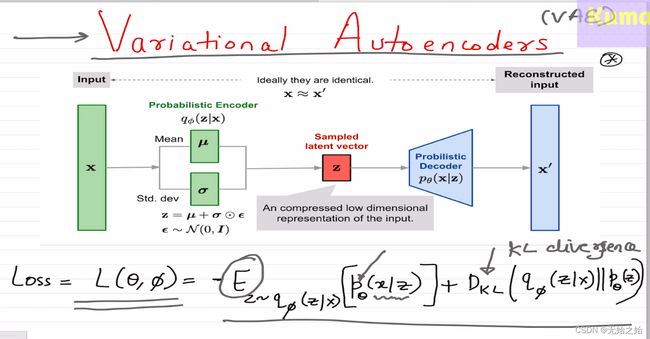
1.2 Variational AutoEncoder 结构
VAE的主要结构与Stacked AutoEncoder的别无二致,区别在于,使用了概率论的相关知识去实现编码器,和解码器,而bottleneck部分则是通过才采样获得的。想要完全理解VAE,其核心在于理解Loss函数的构成。
2. 预备知识
废话不多说,我们先来充一下电,补充点预备知识,正如标题所说,是零点五起步的学习笔记,因此对某些内容将不做进一步的介绍。
2.1 概率
2.1.1 概率分布
p ( x ) p(x) p(x):随机变量 x x x的概率。试想,如果一个变量是随机变化阴晴不定的,那我们应该如何描述和使用它?答案是期望,我们可以简单地认为一个随机变量的期望是确定的,具有统计学意义的(粗糙地理解为可被用于计算的)。一个随机变量的期望的计算公式可以有多种写法,离散的,连续的,还有各种简化的表示方法,下面我们将它用等号串起来:
E p [ x ] = E x ∼ p [ x ] = ∫ x p ( x ) d x = ∑ i k x i p ( x i ) \mathbb{E}_p\left[x\right] = \mathbb{E}_{x\sim p}\left[x\right] = \int xp(x)dx = \sum_i^k x_ip(x_i) Ep[x]=Ex∼p[x]=∫xp(x)dx=i∑kxip(xi)
由上式,可以理解为一个随机变量的期望就是这个变量沿着概率分布的加权平均。其中,离散的概率分布函数简称pmf (probability mass function),而连续的概率的分布函数简称pdf (probability density function)
2.1.2 条件概率
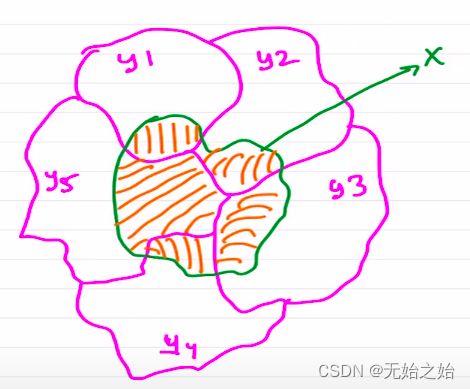
p ( x ∣ y ) p(x|y) p(x∣y):当 y y y事件发生(随机变量确定)时,随机变量 x x x的概率,也被称为条件概率。如下图不难理解,在不同事件发生的时候,x的概率是不同的。也就是说,由于引入了更多的信息(如哪个 y y y事件发生了), x x x时间发生的概率也会随之更新,从而给出相对而言更加准确的预测。
2.1.3 贝叶斯定理 (Baye’s theorem)
贝叶斯定理的公式如下,其中 p ( y ∣ x ) p(y|x) p(y∣x)表示后验概率posterier probability, p ( y ) p(y) p(y)表示先验概率prior probability, p ( x ∣ y ) p ( x ) \frac{p(x|y)}{p(x)} p(x)p(x∣y)表示可能性比例likelihood ratio, p ( x , y ) p(x, y) p(x,y)叫联合概率分布joint probability distribution。
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) p ( x ) = p ( x , y ) p ( x ) \begin{equation} \begin{aligned} p(y|x) &= \frac{p(x|y)p(y)}{p(x)}= \frac{p(x, y)}{p(x)}\\ \end{aligned} \end{equation} p(y∣x)=p(x)p(x∣y)p(y)=p(x)p(x,y)
那么贝叶斯定理具体是怎么应用于生活实践中的呢?总的来说就是模型求逆的过程。首先我们得到一堆有 x x x有 y y y的数据, y y y是天气类型,如晴天,阴天,多云,大雨,暴雨等, x x x为前一天的气象参数,如气压,温度,湿度,风速等相关的信息。我们采集到了今天的气象数据 x x x,明天应该是什么天气?这个问题在贝叶斯定理看来就是求解 p ( y ∣ x ) p(y|x) p(y∣x)的问题。我们可以通过历史数据,统计出不同天气出现的概率 p ( y ) p(y) p(y),以及出现不同天气时,前一天的气象参数出现的概率 p ( x ∣ y ) p(x|y) p(x∣y)。这时候,距离获得 p ( y ∣ x ) p(y|x) p(y∣x)仅仅一步之遥,也就是利用下面的全概率定理求解出不同气象参数出现的概率 p ( x ) p(x) p(x)。
2.1.4 全概率定理(Theorem of total probability)
假设 y i y_i yi(i=1,…,N)为N个互斥事件,那么 x x x事件发生的概率为:
p ( x ) = ∑ i N p ( x ∣ y i ) p ( y i ) p(x)=\sum_i^N p(x|y_i)p(y_i) p(x)=i∑Np(x∣yi)p(yi)
因此,上面的贝叶斯公式也可以写为:
p ( y ∣ x ) = p ( x ∣ y ) p ( y ) ∑ i N p ( x ∣ y i ) p ( y i ) \begin{equation} p(y|x) = \frac{p(x|y)p(y)}{\sum_i^N p(x|y_i)p(y_i)} \end{equation} p(y∣x)=∑iNp(x∣yi)p(yi)p(x∣y)p(y)
2.2 矩阵迹计算技巧
- 如果 x x x是一个标量,那么他的期望等于他的迹, E [ x ] = E [ t r ( x ) ] \mathbb{E}[x]=\mathbb{E}[tr(x)] E[x]=E[tr(x)]
- 设 A , B , C A, B, C A,B,C维度兼容的矩阵,那么矩阵的运算满足,期望和迹可交换,迹中的三个连乘矩阵可按序循环交换:
t r ( A B ) = t r ( B A ) t r ( A B C ) = t r ( B C A ) = t r ( C A B ) E [ t r ( x ) ] = t r ( E [ x ] ) \begin{equation} \begin{aligned} tr(AB) =&~tr(BA)\\ tr(ABC) =&~tr(BCA) = tr(CAB) \\ \mathbb{E}[tr(x)] =&~tr(\mathbb{E}[x]) \end{aligned} \end{equation} tr(AB)=tr(ABC)=E[tr(x)]= tr(BA) tr(BCA)=tr(CAB) tr(E[x]) - 期望计算的变换
E [ x T A x ] = E [ t r ( x T A x ) ] = E [ t r ( A x x T ) ] = t r ( E [ A x x T ] ) \mathbb{E}[x^TAx] =~\mathbb{E}[tr(x^TAx)] = \mathbb{E}[tr(Axx^T)] = tr(\mathbb{E}[Axx^T]) E[xTAx]= E[tr(xTAx)]=E[tr(AxxT)]=tr(E[AxxT])
2.3 KL散度 (Kullback-Leibler Divergence)
2.3.1 介绍
正常人看到KL都会想要问一句,什么是KL散度?从名字上面确实是看不出KL表达的是什么意思的,因为K->Kullback, L->Leibler是KL散度提出者名字的首字母,而散度divergence,可以理解为散开的程度。KL散度是计算两个概率分布之间的距离的度量。也就是说,两个概率分布相差约大,这个计算值因该越大,反之则越小,下面是计算公式:
D K L ( P ∣ ∣ Q ) = ∑ x P ( x ) l o g ( P ( x ) Q ( x ) ) \begin{equation} \mathbb{D}_{KL}\left(P||Q\right) = \sum_x P(x)log\left(\frac{P(x)}{Q(x)}\right) \end{equation} DKL(P∣∣Q)=x∑P(x)log(Q(x)P(x))
- 例子: 假设有离散事件 x x x的可能取值为{0, 1, 2}, 概率分布 P ( x ) P(x) P(x)中 P ( 0 ) = 0.36 , P ( 1 ) = 0.48 , P ( 2 ) = 0.16 P(0)=0.36, P(1)=0.48, P(2)=0.16 P(0)=0.36,P(1)=0.48,P(2)=0.16, 概率分布 Q ( x ) Q(x) Q(x)中 Q ( 0 ) = Q ( 1 ) = Q ( 2 ) = 1 3 Q(0)=Q(1)=Q(2)=\frac{1}{3} Q(0)=Q(1)=Q(2)=31. 则 P P P和 Q Q Q的KL散度是多少?
我们已经是有计算机且会简单写点Python的成年人了,当然编程安排一下:
'''
Author : Dianye Huang
Date : 2022-08-23 10:04:45
LastEditors : Dianye Huang
LastEditTime : 2022-08-23 10:21:41
Description :
'''
import math
class MetricZoo(object):
def __init__(self) -> None:
pass
@staticmethod
def D_KL(P:list, Q:list):
'''
Description:
Kullback-Leibler Divegence which computes the distance
between two probability distributions.
@ param : P{list} -- list of distribution
@ param : Q{list} -- list of distribution
@ return: dkl{float} -- a scalar
'''
dkl = 0
for p, q in zip(P, Q):
dkl += p*math.log(p/q) # in math module, log -> ln
return dkl
if __name__ == '__main__':
mz = MetricZoo()
P = [0.36, 0.48, 0.16]
Q = [1/3]*3
KL_P_Q = round(mz.D_KL(P, Q), 5)
KL_Q_P = round(mz.D_KL(Q, P), 5)
print(f'D_KL(P||Q): {KL_P_Q}')
print(f'D_KL(Q||P): {KL_Q_P}')
''' ----- output
D_KL(P||Q): 0.0853
D_KL(Q||P): 0.09746
'''
2.3.2 KL散度的属性(properties):
- D K L ( P ∣ ∣ Q ) ≥ 0 \mathbb{D}_{KL} (P||Q) \ge 0 DKL(P∣∣Q)≥0, D K L ( Q ∣ ∣ P ) ≥ 0 \mathbb{D}_{KL} (Q||P) \ge 0 DKL(Q∣∣P)≥0
- D K L ( P ∣ ∣ Q ) ≠ D K L ( Q ∣ ∣ P ) \mathbb{D}_{KL} (P||Q) \neq \mathbb{D}_{KL} (Q||P) DKL(P∣∣Q)=DKL(Q∣∣P), 不满足对称性, 如上面代码的例子
2.3.3 多变量正态分布之间的KL散度计算
条件:
计算两个多变量正态分布(multi-variate normal distributions) p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)之间的KL散度。
p ( x ) = N ( x ; μ 1 , Σ 1 ) q ( x ) = N ( x ; μ 2 , Σ 2 ) N ( x ; μ , Σ ) = 1 ( 2 π ) k ∣ Σ ∣ e x p ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) \begin{equation} \begin{aligned} p(x) &= \mathcal{N}(x; \mu_1, \Sigma_1) \\ q(x) &= \mathcal{N}(x; \mu_2, \Sigma_2) \\ \mathcal{N}(x;\mu, \Sigma) &= \frac{1}{\sqrt{(2\pi)^k|\Sigma|}}exp\left(-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\right) \end{aligned} \end{equation} p(x)q(x)N(x;μ,Σ)=N(x;μ1,Σ1)=N(x;μ2,Σ2)=(2π)k∣Σ∣1exp(−21(x−μ)TΣ−1(x−μ))
其中, μ 1 \mu_1 μ1, μ 2 \mu_2 μ2为均值, Σ 1 \Sigma_1 Σ1, Σ 2 \Sigma_2 Σ2为协方差矩阵, x ∈ R k x\in\mathbb{R}^k x∈Rk为满足分布的随机变量, ∣ Σ ∣ |\Sigma| ∣Σ∣ 表示 Σ \Sigma Σ的行列式。
结论:
p ( x ) p(x) p(x)和 q ( x ) q(x) q(x)的KL散度为:
D K L ( p ( x ) ∣ ∣ q ( x ) ) = 1 2 [ l o g ( ∣ Σ 2 ∣ ∣ Σ 1 ∣ ) − k + t r ( Σ 2 − 1 Σ 1 ) + ( μ 2 − μ 1 ) T Σ 2 − 1 ( μ 2 − μ 1 ) ] \begin{equation} \begin{aligned} \mathbb{D}_{KL}\left(p(x)||q(x)\right) =\frac{1}{2}\left[log\left(\frac{|\Sigma_2|}{|\Sigma_1|}\right) - k + tr\left(\Sigma_2^{-1}\Sigma_1\right)+(\mu_2-\mu_1)^T\Sigma_2^{-1}(\mu_2-\mu_1)\right] \end{aligned} \end{equation} DKL(p(x)∣∣q(x))=21[log(∣Σ1∣∣Σ2∣)−k+tr(Σ2−1Σ1)+(μ2−μ1)TΣ2−1(μ2−μ1)]
证明:
直接将两个概率分布的表达式套入KL散度的公式中,然后展开简化后即可得到结论的公式,这里需要应用到很多矩阵迹的运算技巧,在上一节的预备知识中可以查到。
l o g P ( x ) = − k 2 l o g ( 2 π ) − 1 2 l o g ( ∣ Σ 1 ∣ ) − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) l o g Q ( x ) = − k 2 l o g ( 2 π ) − 1 2 l o g ( ∣ Σ 2 ∣ ) − 1 2 ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) μ 1 = E p [ x ] = ∑ x P ( x ) x Σ 1 = E p [ ( x − μ 1 ) ( x − μ 1 ) T ] \begin{equation} \begin{aligned} log~P(x)=&-\frac{k}{2}log(2\pi)\ - \frac{1}{2}log(|\Sigma_1|)-\frac{1}{2}(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)\\ log~Q(x)=&-\frac{k}{2}log(2\pi)\ - \frac{1}{2}log(|\Sigma_2|)-\frac{1}{2}(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2)\\ \mu_1 =& \mathbb{E}_p[x] = \sum_x P(x)x\\ \Sigma_1 = & \mathbb{E}_p[(x-\mu_1)(x-\mu_1)^T] \end{aligned} \end{equation} log P(x)=log Q(x)=μ1=Σ1=−2klog(2π) −21log(∣Σ1∣)−21(x−μ1)TΣ1−1(x−μ1)−2klog(2π) −21log(∣Σ2∣)−21(x−μ2)TΣ2−1(x−μ2)Ep[x]=x∑P(x)xEp[(x−μ1)(x−μ1)T]
带入上式,可得:
D K L ( P ∣ ∣ Q ) = ∑ x P ( x ) l o g ( P ( x ) Q ( x ) ) = ∑ x P ( x ) ( l o g P ( x ) − l o g Q ( x ) ) = ∑ x P ( x ) ( − k 2 l o g ( 2 π ) − 1 2 l o g ( ∣ Σ 1 ∣ ) − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) + k 2 l o g ( 2 π ) + 1 2 l o g ( ∣ Σ 2 ∣ ) + 1 2 ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) ) ) = ∑ x P ( x ) ( 1 2 l o g ( ∣ Σ 2 ∣ ∣ Σ 1 ∣ ) − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) + 1 2 ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) ) \begin{equation} \begin{aligned} \mathbb{D}_{KL}\left(P||Q\right) =& \sum_x P(x)log\left(\frac{P(x)}{Q(x)}\right) \\ =&\sum_x P(x)\left(log~P(x) - log~Q(x)\right)\\ =&\sum_x P(x)\bigg(-\frac{k}{2}log(2\pi)\ - \frac{1}{2}log(|\Sigma_1|)-\frac{1}{2}(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1) \\ &+\frac{k}{2}log(2\pi)\ + \frac{1}{2}log(|\Sigma_2|)+\frac{1}{2}(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2)) \bigg)\\ =&\sum_x P(x)\bigg(\frac{1}{2}log\left(\frac{|\Sigma_2|}{|\Sigma_1|}\right)-\frac{1}{2}(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)+\frac{1}{2}(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2) \bigg)\\ \end{aligned} \end{equation} DKL(P∣∣Q)====x∑P(x)log(Q(x)P(x))x∑P(x)(log P(x)−log Q(x))x∑P(x)(−2klog(2π) −21log(∣Σ1∣)−21(x−μ1)TΣ1−1(x−μ1)+2klog(2π) +21log(∣Σ2∣)+21(x−μ2)TΣ2−1(x−μ2)))x∑P(x)(21log(∣Σ1∣∣Σ2∣)−21(x−μ1)TΣ1−1(x−μ1)+21(x−μ2)TΣ2−1(x−μ2))
接下来的简化大法就需要用到矩阵迹的运算公式了,精华都在这张PPT中:
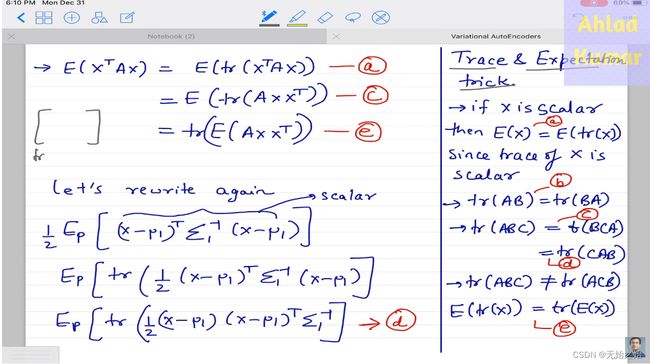
D K L ( P ∣ ∣ Q ) = ∑ x P ( x ) ( 1 2 l o g ( ∣ Σ 2 ∣ ∣ Σ 1 ∣ ) − 1 2 ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) + 1 2 ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) ) = 1 2 l o g ( ∣ Σ 2 ∣ ∣ Σ 1 ∣ ) − 1 2 E p [ ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] + 1 2 E p [ ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) ] \begin{equation} \begin{aligned} \mathbb{D}_{KL}\left(P||Q\right) =&\sum_x P(x)\bigg(\frac{1}{2}log\left(\frac{|\Sigma_2|}{|\Sigma_1|}\right)-\frac{1}{2}(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)+\frac{1}{2}(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2) \bigg)\\ =&\frac{1}{2}log\left(\frac{|\Sigma_2|}{|\Sigma_1|}\right) - \frac{1}{2}\mathbb{E}_p\left[(x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)\right] + \frac{1}{2}\mathbb{E}_p\left[(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2)\right]\\ \end{aligned} \end{equation} DKL(P∣∣Q)==x∑P(x)(21log(∣Σ1∣∣Σ2∣)−21(x−μ1)TΣ1−1(x−μ1)+21(x−μ2)TΣ2−1(x−μ2))21log(∣Σ1∣∣Σ2∣)−21Ep[(x−μ1)TΣ1−1(x−μ1)]+21Ep[(x−μ2)TΣ2−1(x−μ2)]
其中,第一项期望展开后为:
E p [ − ( x − μ 1 ) T Σ 1 − 1 ( x − μ 1 ) ] = E p [ t r ( ( x − μ 1 ) ( x − μ 1 ) T Σ 1 − 1 ) ] = t r ( E p [ ( x − μ 1 ) ( x − μ 1 ) T ] Σ 1 − 1 ) = t r ( Σ 1 Σ 1 − 1 ) = t r ( I k ) = k \begin{equation} \begin{aligned} &\mathbb{E}_p\left[- (x-\mu_1)^T\Sigma_1^{-1}(x-\mu_1)\right] \\ =& ~\mathbb{E}_p\left[tr\left((x-\mu_1) (x-\mu_1)^T\Sigma_1^{-1}\right)\right] \\ =& ~tr\left(\mathbb{E}_p\left[(x-\mu_1) (x-\mu_1)^T\right]\Sigma_1^{-1}\right)\\ =& ~tr\left(\Sigma_1\Sigma_1^{-1}\right)\\ =& ~tr(I_k)\\ =& ~k \end{aligned} \end{equation} =====Ep[−(x−μ1)TΣ1−1(x−μ1)] Ep[tr((x−μ1)(x−μ1)TΣ1−1)] tr(Ep[(x−μ1)(x−μ1)T]Σ1−1) tr(Σ1Σ1−1) tr(Ik) k
第二项期望展开后为:
1 2 E p [ ( x − μ 2 ) T Σ 2 − 1 ( x − μ 2 ) ] = E p { 1 2 [ ( x − μ 1 ) + ( μ 1 − μ 2 ) ] T Σ 2 − 1 [ ( x − μ 1 ) + ( μ 1 − μ 2 ) ] } = E p { 1 2 ( x − μ 1 ) T Σ 2 − 1 ( x − μ 1 ) + ( x − μ 1 ) T Σ 2 − 1 ( μ 1 − μ 2 ) + 1 2 ( μ 1 − μ 2 ) T Σ 2 − 1 ( μ 1 − μ 2 ) } = t r { E p [ 1 2 Σ 2 − 1 ( x − μ 1 ) ( x − μ 1 ) T ] } + t r { ( E p [ x ] − μ 1 ) T Σ 2 − 1 ( μ 1 − μ 2 ) } + 1 2 ( μ 1 − μ 2 ) T Σ 2 − 1 ( μ 1 − μ 2 ) = t r { Σ 2 − 1 Σ 1 2 } + 0 + 1 2 ( μ 1 − μ 2 ) T Σ 2 − 1 ( μ 1 − μ 2 ) \begin{equation} \begin{aligned} &\frac{1}{2}\mathbb{E}_p\left[(x-\mu_2)^T\Sigma_2^{-1}(x-\mu_2)\right] \\ =& \mathbb{E}_p\left\{ \frac{1}{2}\left[(x-\mu_1) + (\mu_1-\mu_2)\right]^T\Sigma_2^{-1}\left[(x-\mu_1) + (\mu_1-\mu_2)\right]\right\} \\ =& \mathbb{E}_p \left\{\frac{1}{2} (x-\mu_1) ^T\Sigma^{-1}_2(x-\mu_1) + (x-\mu_1)^T\Sigma_2^{-1}(\mu_1-\mu_2) + \frac{1}{2} (\mu_1-\mu_2)^T\Sigma^{-1}_2(\mu_1-\mu_2) \right\}\\ =&tr\left\{\mathbb{E}_p \left[\frac{1}{2}\Sigma^{-1}_2(x-\mu_1)(x-\mu_1) ^T\right]\right\} + tr\left\{\left(\mathbb{E}_p[x]-\mu_1\right)^T\Sigma_2^{-1}(\mu_1-\mu_2) \right\} + \frac{1}{2}(\mu_1-\mu_2)^T\Sigma^{-1}_2(\mu_1-\mu_2)\\ =& tr\left\{\frac{\Sigma_2^{-1}\Sigma_1}{2}\right\} + 0 + \frac{1}{2}(\mu_1-\mu_2)^T\Sigma^{-1}_2(\mu_1-\mu_2)\\ \end{aligned} \end{equation} ====21Ep[(x−μ2)TΣ2−1(x−μ2)]Ep{21[(x−μ1)+(μ1−μ2)]TΣ2−1[(x−μ1)+(μ1−μ2)]}Ep{21(x−μ1)TΣ2−1(x−μ1)+(x−μ1)TΣ2−1(μ1−μ2)+21(μ1−μ2)TΣ2−1(μ1−μ2)}tr{Ep[21Σ2−1(x−μ1)(x−μ1)T]}+tr{(Ep[x]−μ1)TΣ2−1(μ1−μ2)}+21(μ1−μ2)TΣ2−1(μ1−μ2)tr{2Σ2−1Σ1}+0+21(μ1−μ2)TΣ2−1(μ1−μ2)
带入上面所有的公式,最终可得:
D K L ( P ∣ ∣ Q ) = 1 2 l o g ( ∣ Σ 2 ∣ ∣ Σ 1 ∣ ) − k 2 + t r { Σ 1 − 1 Σ 2 − 1 2 } + 1 2 ( μ 1 − μ 2 ) T Σ 2 − 1 ( μ 1 − μ 2 ) = 1 2 [ l o g ( ∣ Σ 2 ∣ ∣ Σ 1 ∣ ) − k + t r ( Σ 2 − 1 Σ 1 ) + ( μ 2 − μ 1 ) T Σ 2 − 1 ( μ 2 − μ 1 ) ] \begin{equation} \begin{aligned} \mathbb{D}_{KL}\left(P||Q\right) =& \frac{1}{2}log\left(\frac{|\Sigma_2|}{|\Sigma_1|}\right) - \frac{k}{2}+ tr\left\{\frac{\Sigma_1^{-1}\Sigma_2^{-1}}{2}\right\} + \frac{1}{2}(\mu_1-\mu_2)^T\Sigma^{-1}_2(\mu_1-\mu_2) \\ =&\frac{1}{2}\left[log\left(\frac{|\Sigma_2|}{|\Sigma_1|}\right) - k + tr\left(\Sigma_2^{-1}\Sigma_1\right) + (\mu_2-\mu_1)^T\Sigma^{-1}_2(\mu_2-\mu_1)\right] \end{aligned} \end{equation} DKL(P∣∣Q)==21log(∣Σ1∣∣Σ2∣)−2k+tr{2Σ1−1Σ2−1}+21(μ1−μ2)TΣ2−1(μ1−μ2)21[log(∣Σ1∣∣Σ2∣)−k+tr(Σ2−1Σ1)+(μ2−μ1)TΣ2−1(μ2−μ1)]
3. 总结
这篇博客主要记录了如何VAE的一些预备知识,尤其是记录了两个多变量正态分布的KL散度的计算的详细推导。后面的笔记将主要关注VAE提出的动机和主要思想,VAE网络权值优化的公式推导,VAE的编程实现,最后再过渡到cVAE。
最后,祝诸君周中愉快!
2022年8月24日
Dianye Huang