论文阅读笔记（RethinkDIP):Rethinking Deep Image Prior for Denoising

Rethinking Deep Image Prior for Denoising

论文地址：https://arxiv.org/abs/2108.12841

代码地址：GitHub - gistvision/DIP-denosing: Code and models for “Rethinking Deep Image Prior for Denoising” (ICCV 2021)

引用格式：

@inproceedings{jo2021rethinking,
  title={Rethinking Deep Image Prior for Denoising},
  author={Jo, Yeonsik and Chun, Se Young and Choi, Jonghyun},
  booktitle={Proceedings of the IEEE/CVF International Conference on Computer Vision},
  pages={5087--5096},
  year={2021}
}

Abstract

DIP局限性：

1. 对噪声过拟合
2. 没有迭代停止标准

改进点：

1. DF（Degrees of freedom）监控优化过程
2. 过零点停止标准（Zero-crossing stopping criterion）
3. 随机时间集成STE（Stochastic temporal ensembling）
4. 将任务扩充到possion噪声
5. 增加评价标准：学习感知图像块相似度(Learned Perceptual Image Patch Similarity, LPIPS)

Preliminaries

问题描述：

沿用了DIP的思路，$y$为噪声图像，$x$为干净图像，$n$为噪声。

$y=x+n$

参数优化：$\hat{\theta }=\underset{\theta }{\mathrm{argmin}}\mathcal{L}(h(\dot{n};\theta ),y)$

【我的理解此处的$\dot{n}$为DIP中的随机变量$z$】

Effective degrees of freedom(DF):

模型对训练数据的拟合量。

输入：$y$ , $ h(.)$

$DF(h)=\frac{1}{{\sigma }^2}{\sum }_{i=1}^{n}Cov(h_i(.),y_i)$

其中，$Cov$为协方差，$\sigma$为噪声的标准差。

使用Stein’s lemma简化协方差计算：

$\frac{1}{{\sigma }^2}{\sum }_{i=1}^{n}Cov(h_i(.),y_i)=\mathbb{E}[{\sum }_{i=1}^n\frac{\partial h_i(y)}{\partial y_i}]$

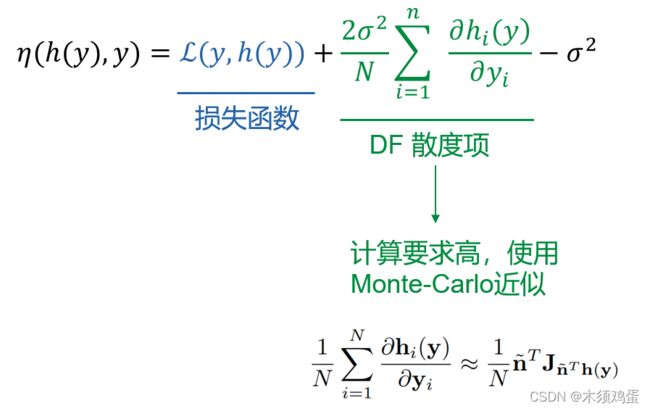
引入Stein’s unbiased risk estimator (SURE)对loss函数进行无偏估计，抑制DF：

$\eta (h(y),y)=L(y,h(y))+\frac{2{\sigma }^2}{N}{\sum }_{i=1}^n\frac{\partial h_i(y)}{\partial y_i}-{\sigma }^2$

分成损失函数与散度项的组合，由于散度项的计算要求依然很高所以使用Monte-Carlo近似。

过零点停止标准(Zero-crossing stopping criterion)：

现象：散度项在收敛前上升，在收敛后发散到$-\infty$。

措施：目标函数偏离零时停止迭代。

随机时间集成(Stochastic temporal ensembling):

• 噪声正则化：在迭代中为输入添加噪声。
  • $\hat{\theta }=\underset{\theta }{\mathrm{argmin}}\mathcal{L}(h(\dot{n}+\gamma ),y)$
  • $\gamma$为噪声向量，$\gamma \sim N(0,{\sigma }_{\gamma }^{2}I)$
• 指数移动平均：对上次迭代获得的恢复图像进行平均。集成操作

将以上两种方法融合得到STE：

$\eta (h(y_2),y_1)=\mathcal{L}(h(y_2),y1)+\frac{2{\sigma }^2}{N}{\sum }_{i=1}^n\frac{\partial h_i(y_2)}{\partial (y_2{)}_i}-{\sigma }^2$

其中，$y_1=y,y_2=y_1+\gamma$，$\sigma$为$y_1$ 的已知噪声水平。$\mathcal{L}(h(y_2),y1)$为数据项，$\frac{2{\sigma }^2}{N}{\sum }_{i=1}^n\frac{\partial h_i(y_2)}{\partial (y_2{)}_i}$为正则项。

关于DF的补充：

DF与模型$h$的估计类似（测试误差与训练误差之间的差异）：

$\rho (h)=\mathbb{E}[\mathcal{L}(\tilde{y},h(.))-\mathcal{L}(y,h(.))]$

其中，$\mathcal{L}$为MSE Loss，$\tilde{y}$和$y$为不同$n$的噪声图像。

在其他研究中表示$\rho (h)=2{\sum }_{i=1}^{n}Cov(h_i(.),y_i)$

由于$DF(h)=\frac{1}{{\sigma }^2}{\sum }_{i=1}^{n}Cov(h_i(.),y_i)$

因此，$2{\sigma }^2\cdot DF(h)=\rho (h)$

引入DF的简单估计和单个ground truth得到$D{F}_{GT}$:

$2{\sigma }^2\cdot D{F}_{GT}(h)\approx \mathcal{L}(x,h(.))-\mathcal{L}(y,h(.))+{\sigma }^2$

DF越大代表过度拟合了输入$y$。若DIP的结果靠近干净图像$x$，则$D{F}_{GT}$接近于0；若DIP的结果越靠近噪声图像$y$，DF结果越大。【使用这个性质可以分析DIP的优化过程】

思考

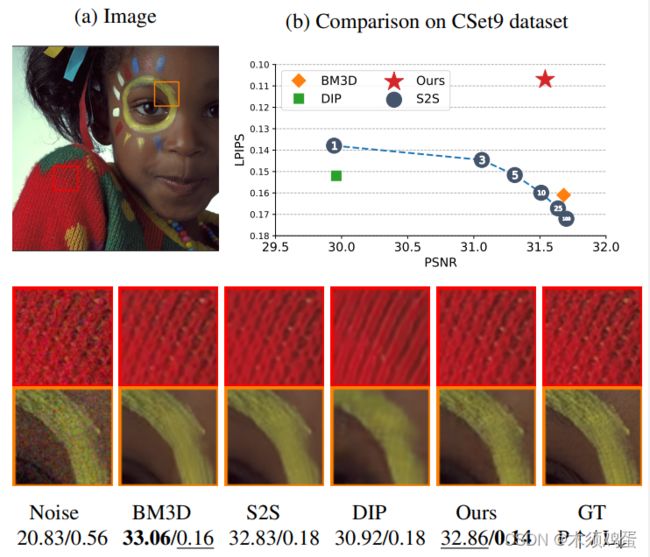
在论文中的Figure1中，选择作为展示的图片，BM3D的去噪效果在PSNR的比较上反而是最佳的，甚至超过了Self2Self。只是在新增加的评价标准LPIPS上本方法最佳。

在实验结果对比中也有体现了类似的现象：

【对于这些新算法需要更多一点辩证的思维来看待，不能完全信任所描述的结果。】

DIP 类方法基于单幅图像，需要对不同 的图像重新训练模型，这样并不符合实际的应用场景。