WGAN (Wasserstein GAN)
Paper: https://arxiv.org/abs/1701.07875
Github:
https://github.com/eriklindernoren/PyTorch-GAN
https://github.com/martinarjovsky/WassersteinGAN
一. 前言
传统GAN存在的问题: 存在训练困难、生成器和判断器的loss无法指示训练过程、生成样本缺乏多样性等问题。
WGAN解决的问题:
- 彻底解决GAN训练不稳定的问题,不再需要小心平衡生成器和判断器的训练程度
- 基本解决了collapse mode的问题,确保了生成样本的多样性
- 训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程,这个数值越小代表GAN训练得越好,代表生成器产生的图像质量越高
- 以上一切好处不需要精心设计的网络结构,最简单的多层全连接网络就可做到
作者花了俩篇论文,第一篇论文中《Towards Principled Methods for Training Generative Adversarial Networks》从理论上分析了原始GAN的问题所在,从而针对性地给出了改进要点;第二篇论文《Wasserstein GAN》里面,又再这个改进点出发,最终给出了改进的算法实现流程,而改进后后相比原始GAN的算法实现流程只改了四点:
- 判断器最后一层去掉Sigmoid
- 生成器和判断器的loss不取log
- 每次更新判断器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行
- 先更新discriminator中的权重,在 n c r i t i c n_{critic} ncritic内不更新generator的权重
- 在更新discriminator的权重的时候,每一步更新完后将权重clip到(-c,c)之中
二.原始的GAN究竟出了什么问题?
原始GAN判断器最小化如下损失函数,尽可能把真实样本分为正例子,生成样本分为负例:
− E x ∼ P r [ log D ( x ) ] − E x ∼ P g [ log ( 1 − D ( x ) ) ] - \mathbb { E } _ { x \sim P _ { r } } [ \log D ( x ) ] - \mathbb { E } _ { x \sim P _ { g } } [ \log ( 1 - D ( x ) ) ] −Ex∼Pr[logD(x)]−Ex∼Pg[log(1−D(x))] (1)
其中 P r P_{r} Pr是真实样本分布, P g P_{g} Pg是由生成器产生的样本分布。对于生成器,Goodfellow一开始提出来一个损失函数,后来又提出了一个改进的损失函数,分别是:
E x ∼ P g [ log ( 1 − D ( x ) ) ] \mathbb { E } _ { x \sim P _ { g } } [ \log ( 1 - D ( x ) ) ] Ex∼Pg[log(1−D(x))] (2)
E x ∼ P g [ − log D ( x ) ] \mathbb { E } _ { x \sim P _ { g } } [ - \log D ( x ) ] Ex∼Pg[−logD(x)] (3)
后者在WGAN俩篇论文中称为“the-log D alternative” 或 “the-log D trick”。WGAN分别分析了这两种形式的原始GAN各自的问题所在,下面分别说明。
第一种原始GAN形式的问题
一句话概括:判别器越好,生成器梯度消失越严重。WGAN前作从两个角度进行了论证,第一个角度是从生成器的等价损失函数切入的。
首先从公式1可以得到,在生成器G固定参数时最优的判别器D应该是什么。对于一个具体的样本x,它可能来自真实分布也可能来自生成分布,它对公式1损失函数的贡献是:
− P r ( x ) log D ( x ) − P g ( x ) log [ 1 − D ( x ) ] - P _ { r } ( x ) \log D ( x ) - P _ { g } ( x ) \log [ 1 - D ( x ) ] −Pr(x)logD(x)−Pg(x)log[1−D(x)]
令其关于 D ( x ) D(x) D(x)的导数为0,得
− P r ( x ) D ( x ) + P g ( x ) 1 − D ( x ) = 0 - \frac { P _ { r } ( x ) } { D ( x ) } + \frac { P _ { g } ( x ) } { 1 - D ( x ) } = 0 −D(x)Pr(x)+1−D(x)Pg(x)=0
化简得最优判断器为:
D ∗ ( x ) = P r ( x ) P r ( x ) + P g ( x ) D ^ { * } ( x ) = \frac { P _ { r } ( x ) } { P _ { r } ( x ) + P _ { g } ( x ) } D∗(x)=Pr(x)+Pg(x)Pr(x) (4)
这个结果从直观上很容易理解,就是看一个样本x来自真实分布和生成分布的可能性的相对比例。如果 P r ( x ) = 0 P_{r}(x)=0 Pr(x)=0且 P g ( x ) ! = 0 P_{g}(x)!=0 Pg(x)!=0,最优判断器就应该非常自信地给出概率0;如果 P r ( x ) = P g ( x ) P_{r}(x)=P_{g}(x) Pr(x)=Pg(x),说明该样本是真是假的可能性刚好一半一半,此时最优判别器也应该给出概率0.5。
然而GAN训练有一个trick,就是别把判别器训练得太好,否则在实验中生成器会完全学不动(loss降不下去),为了探究背后的原因,我们就可以看看在极端情况——判别器最优时,生成器的损失函数变成什么。给公式2加上一个不依赖于生成器的项,使之变成
E x ∼ P r [ log D ( x ) ] + E x ∼ P g [ log ( 1 − D ( x ) ) ] \mathbb { E } _ { x \sim P _ { r } } [ \log D ( x ) ] + \mathbb { E } _ { x \sim P _ { g } } [ \log ( 1 - D ( x ) ) ] Ex∼Pr[logD(x)]+Ex∼Pg[log(1−D(x))]
注意,最小化这个损失函数等价于最小化公式2,而且它刚好是判别器损失函数的反。代入最优判别器即公式4,再进行简单的变换可以得到
E x ∼ P r log P r ( x ) 1 2 [ P r ( x ) + P g ( x ) ] + E x ∼ P g log P g ( x ) 1 2 [ P r ( x ) + P g ( x ) ] − 2 log 2 \mathbb { E } _ { x \sim P _ { r } } \log \frac { P _ { r } ( x ) } { \frac { 1 } { 2 } \left[ P _ { r } ( x ) + P _ { g } ( x ) \right] } + \mathbb { E } _ { x \sim P _ { g } } \log \frac { P _ { g } ( x ) } { \frac { 1 } { 2 } \left[ P _ { r } ( x ) + P _ { g } ( x ) \right] } - 2 \log 2 Ex∼Prlog21[Pr(x)+Pg(x)]Pr(x)+Ex∼Pglog21[Pr(x)+Pg(x)]Pg(x)−2log2 (公式5)
变换成这个样子是为了引入Kullback–Leibler divergence(简称KL散度)和Jensen-Shannon divergence(简称JS散度)这两个重要的相似度衡量指标,后面的主角之一Wasserstein距离,就是要来吊打它们两个的。所以接下来介绍这两个重要的配角——KL散度和JS散度:
KL散度,又称KL距离,相对熵。
K L ( P 1 ∥ P 2 ) = E x ∼ P 1 log P 1 P 2 K L \left( P _ { 1 } \| P _ { 2 } \right) = \mathbb { E } _ { x \sim P _ { 1 } } \log \frac { P _ { 1 } } { P _ { 2 } } KL(P1∥P2)=Ex∼P1logP2P1 (公式6)
即 K L ( P 1 ∥ P 2 ) = ∑ P 1 ( x ) log P 1 ( x ) P 2 ( x ) \mathrm { KL} ( \mathrm { P_{1} } \| \mathrm { P_{2} } ) = \sum P _{1}( x ) \log \frac { P_{1} ( x ) } { P_{2} ( x ) } KL(P1∥P2)=∑P1(x)logP2(x)P1(x),当 P ( x ) P(x) P(x)和 Q ( x ) Q(x) Q(x)的相似度越高,KL散度越小
JS散度,也称JS距离,是KL散度的一种变形。JS散度的值域范围是[0,1],相同则是0,相反为1。相较于KL,对相似度的判别更确切了。
J S ( P 1 ∥ P 2 ) = 1 2 K L ( P 1 ∥ P 1 + P 2 2 ) + 1 2 K L ( P 2 ∥ P 1 + P 2 2 ) J S \left( P _ { 1 } \| P _ { 2 } \right) = \frac { 1 } { 2 } K L \left( P _ { 1 } \| \frac { P _ { 1 } + P _ { 2 } } { 2 } \right) + \frac { 1 } { 2 } K L \left( P _ { 2 } \| \frac { P _ { 1 } + P _ { 2 } } { 2 } \right) JS(P1∥P2)=21KL(P1∥2P1+P2)+21KL(P2∥2P1+P2) (公式7)
于是公式5就可以继续写成
2 J S ( P r ∥ P g ) − 2 log 2 2 J S \left( P _ { r } \| P _ { g } \right) - 2 \log 2 2JS(Pr∥Pg)−2log2 (公式8)
于是得到结论:
根据原始GAN定义的判别器loss,我们可以得到最优判别器的形式;而在最优判别器的下,我们可以把原始GAN定义的生成器loss等价变换为最小化真实分布 P r P_{r} Pr与生成分布 P g P_{g} Pg之间的JS散度。我们越训练判别器,它就越接近最优,最小化生成器的loss也就会越近似于最小化 P r P_{r} Pr和 P g P_{g} Pg之间的JS散度。
而问题就出在了这个JS散度上,我们会希望如果俩个分布之间越接近它们的JS散度越小,我们通过优化JS散度就能将 P { g } P_{g} P{g}“拉向” P r P_{r} Pr,最终以假乱真。这个希望在两个分布有所重叠的时候是成立的,但是如果两个分布完全没有重叠的部分,或者它们重叠的部分可忽略(下面解释什么叫可忽略),它们的JS散度是多少呢?
答案是 l o g 2 log 2 log2,因为对于任意一个x只有四种可能:
P 1 ( x ) = 0 P1(x)=0 P1(x)=0且 P 2 ( x ) = 0 P_{2}(x)=0 P2(x)=0
P 1 ( x ) ≠ 0 P1(x)\neq 0 P1(x)̸=0且 P 2 ( x ) ≠ 0 P_{2}(x) \neq 0 P2(x)̸=0
P 1 ( x ) = 0 P1(x)=0 P1(x)=0且 P 2 ( x ) ≠ 0 P_{2}(x) \neq 0 P2(x)̸=0
P 1 ( x ) ≠ 0 P1(x) \neq 0 P1(x)̸=0且 P 2 ( x ) = 0 P_{2}(x)=0 P2(x)=0
第一种对计算JS散度无贡献,第二种情况由于重叠部分可忽略所以贡献也为0,第三种情况对公式7右边第一个项的贡献是 log P 2 1 2 ( P 2 + 0 ) = log 2 \log \frac { P _ { 2 } } { \frac { 1 } { 2 } \left( P _ { 2 } + 0 \right) } = \log 2 log21(P2+0)P2=log2, 第四种情况与之类似,所以最终 J S ( P 1 ∥ P 2 ) = − log 2 J S \left( P _ { 1 } \| P _ { 2 } \right) = -\log 2 JS(P1∥P2)=−log2
换句话说,无论 P r P_{r} Pr跟 P g P_{g} Pg 是远在天边,还是近在眼前,只要它们俩没有一点重叠或者重叠部分可忽略,JS散度就固定是常数 − log 2 -\log 2 −log2,而这对于梯度下降方法意味着——梯度为0!此时对于最优判别器来说,生成器肯定是得不到一丁点梯度信息的;即使对于接近最优的判别器来说,生成器也有很大机会面临梯度消失的问题。
但是 P r P_{r} Pr与 P g P_{g} Pg不重叠或重叠部分可忽略的可能性有多大?不严谨的答案是:非常大。比较严谨的答案是:当 P r P_{r} Pr与 P g P_{g} Pg的支撑集(support)是高维空间中的低维流形(manifold)时, P r P_{r} Pr与 P g P_{g} Pg重叠部分测度(measure)为0的概率为1。
虽然论文给出的是严格的数学表述,但是直观上其实很容易理解。首先简单介绍一下这几个概念:
- 支撑集(support)其实就是函数的非零部分子集,比如ReLU函数的支撑集就是(0, + ∞ \infty ∞),一个概率分布的支撑集就是所有概率密度非零部分的集合。
- 流形(manifold)是高维空间中曲线、曲面概念的拓广,我们可以在低维上直观理解这个概念,比如我们说三维空间中的一个曲面是一个二维流形,因为它的本质维度(intrinsic dimension)只有2,一个点在这个二维流形上移动只有两个方向的自由度。同理,三维空间或者二维空间中的一条曲线都是一个一维流形。
- 测度(measure)是高维空间中长度、面积、体积概念的拓广,可以理解为“超体积”。
回过头来看第一句话,“当P_r与P_g的支撑集是高维空间中的低维流形时”,基本上是成立的。回过头来看第一句话,“当P_r与P_g的支撑集是高维空间中的低维流形时”,基本上是成立的。原因是GAN中的生成器一般是从某个低维(比如100维)的随机分布中采样出一个编码向量,再经过一个神经网络生成出一个高维样本(比如64x64的图片就有4096维)。当生成器的参数固定时,生成样本的概率分布虽然是定义在4096维的空间上,但它本身所有可能产生的变化已经被那个100维的随机分布限定了,其本质维度就是100,再考虑到神经网络带来的映射降维,最终可能比100还小,所以生成样本分布的支撑集就在4096维空间中构成一个最多100维的低维流形,“撑不满”整个高维空间。
“撑不满”就会导致真实分布与生成分布难以“碰到面”,这很容易在二维空间中理解:一方面,二维平面中随机取两条曲线,它们之间刚好存在重叠线段的概率为0;另一方面,虽然它们很大可能会存在交叉点,但是相比于两条曲线而言,交叉点比曲线低一个维度,长度(测度)为0,可忽略。三维空间中也是类似的,随机取两个曲面,它们之间最多就是比较有可能存在交叉线,但是交叉线比曲面低一个维度,面积(测度)是0,可忽略。从低维空间拓展到高维空间,就有了如下逻辑:因为一开始生成器随机初始化,所以 P g P_{g} Pg几乎不可能与 P r P_{r} Pr有什么关联,所以它们的支撑集之间的重叠部分要么不存在,要么就比 P r P_{r} Pr和 P g P_{g} Pg的最小维度还要低至少一个维度,故而测度为0。所谓“重叠部分测度为0”,就是上文所言“不重叠或者重叠部分可忽略”的意思。
我们就得到了WGAN前作中关于生成器梯度消失的第一个论证:在(近似)最优判别器下,最小化生成器的loss等价于最小化P_r与P_g之间的JS散度,而由于 P r P_{r} Pr与 P g P_{g} Pg几乎不可能有不可忽略的重叠,所以无论它们相距多远JS散度都是常数 − l o g 2 -log 2 −log2,最终导致生成器的梯度(近似)为0,梯度消失。
有了这些理论分析,原始GAN不稳定的原因就彻底清楚了:判别器训练得太好,生成器梯度消失,生成器loss降不下去;判别器训练得不好,生成器梯度不准,四处乱跑。只有判别器训练得不好不坏才行,但是这个火候又很难把握,甚至在同一轮训练的前后不同阶段这个火候都可能不一样,所以GAN才那么难训练。
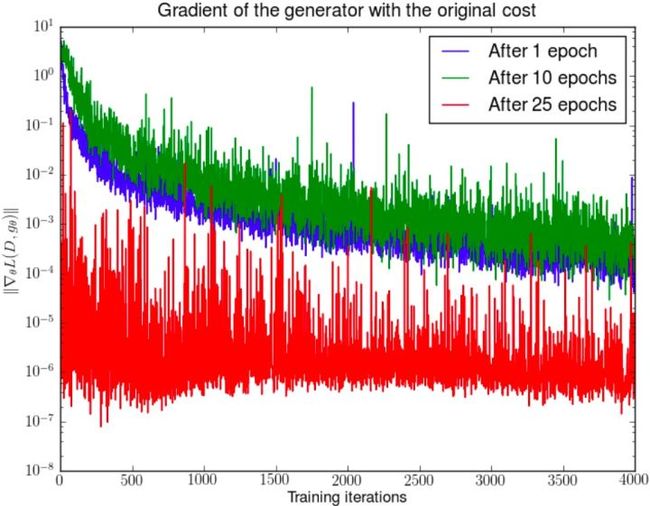
WGAN前作Figure 2。先分别将DCGAN训练1,20,25个epoch,然后固定生成器不动,判别器重新随机初始化从头开始训练,对于第一种形式的生成器loss产生的梯度可以打印出其尺度的变化曲线,可以看到随着判别器的训练,生成器的梯度均迅速衰减。注意y轴是对数坐标轴。
第二种原始GAN形式的问题
一句话概括:最小化第二种生成器loss函数,会等价于最小化一个不合理的距离衡量,导致两个问题,一是梯度不稳定,二是collapse mode即多样性不足。WGAN前作又是从两个角度进行了论证,下面只说第一个角度。
如前文所说,Ian Goodfellow提出的“- log D trick”是把生成器loss改成
E x ∼ P g [ − log D ( x ) ] \mathbb { E } _ { x \sim P _ { g } } [ - \log D ( x ) ] Ex∼Pg[−logD(x)] (公式3)
上文已经推导已经得到在最优判断器 D ∗ D ^ { * } D∗下
E x ∼ P r [ log D ∗ ( x ) ] + E x ∼ P g [ log ( 1 − D ∗ ( x ) ) ] = 2 J S ( P r ∥ P g ) − 2 log 2 \mathbb { E } _ { x \sim P _ { r } } \left[ \log D ^ { * } ( x ) \right] + \mathbb { E } _ { x \sim P _ { g } } \left[ \log \left( 1 - D ^ { * } ( x ) \right) \right] = 2 J S \left( P _ { r } \| P _ { g } \right) - 2 \log 2 Ex∼Pr[logD∗(x)]+Ex∼Pg[log(1−D∗(x))]=2JS(Pr∥Pg)−2log2 (公式9)
我们可以把KL散度(注意下面是先g后r)变换成含 D ∗ D^{*} D∗的形式:
K L ( P g ∥ P r ) = E x ∼ P g [ log P g ( x ) P r ( x ) ] = E x ∼ P g [ log P g ( x ) / ( P r ( x ) + P g ( x ) ) P r ( x ) / ( P r ( x ) + P g ( x ) ) ] = E x ∼ P g [ log 1 − D ∗ ( x ) D ∗ ( x ) ] = E x ∼ P g log [ 1 − D ∗ ( x ) ] − E x ∼ P g log D ∗ ( x ) \begin{aligned} K L \left( P _ { g } \| P _ { r } \right) & = \mathbb { E } _ { x \sim P _ { g } } \left[ \log \frac { P _ { g } ( x ) } { P _ { r } ( x ) } \right] \\ & = \mathbb { E } _ { x \sim P _ { g } } \left[ \log \frac { P _ { g } ( x ) / \left( P _ { r } ( x ) + P _ { g } ( x ) \right) } { P _ { r } ( x ) / \left( P _ { r } ( x ) + P _ { g } ( x ) \right) } \right] \\ & = \mathbb { E } _ { x \sim P _ { g } } \left[ \log \frac { 1 - D ^ { * } ( x ) } { D ^ { * } ( x ) } \right] \\ & = \mathbb { E } _ { x \sim P _ { g } } \log \left[ 1 - D ^ { * } ( x ) \right] - \mathbb { E } _ { x \sim P _ { g } } \log D ^ { * } ( x ) \end{aligned} KL(Pg∥Pr)=Ex∼Pg[logPr(x)Pg(x)]=Ex∼Pg[logPr(x)/(Pr(x)+Pg(x))Pg(x)/(Pr(x)+Pg(x))]=Ex∼Pg[logD∗(x)1−D∗(x)]=Ex∼Pglog[1−D∗(x)]−Ex∼PglogD∗(x) (公式10)
由公式3,9,10可得最小化目标的等价变形
E x ∼ P g [ − log D ∗ ( x ) ] = K L ( P g ∥ P r ) − E x ∼ P g log [ 1 − D ∗ ( x ) ] = K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) + 2 log 2 + E x ∼ P r [ log D ∗ ( x ) ] \begin{aligned} \mathbb { E } _ { x \sim P _ { g } } \left[ - \log D ^ { * } ( x ) \right] & = K L \left( P _ { g } \| P _ { r } \right) - \mathbb { E } _ { x \sim P _ { g } } \log \left[ 1 - D ^ { * } ( x ) \right] \\ & = K L \left( P _ { g } \| P _ { r } \right) - 2 J S \left( P _ { r } \| P _ { g } \right) + 2 \log 2 + \mathbb { E } _ { x \sim P _ { r } } \left[ \log D ^ { * } ( x ) \right] \end{aligned} Ex∼Pg[−logD∗(x)]=KL(Pg∥Pr)−Ex∼Pglog[1−D∗(x)]=KL(Pg∥Pr)−2JS(Pr∥Pg)+2log2+Ex∼Pr[logD∗(x)]
注意上式最后两项不依赖于生成器G,最终得到最小化公式3等价于最小化
K L ( P g ∥ P r ) − 2 J S ( P r ∥ P g ) K L \left( P _ { g } \| P _ { r } \right) - 2 J S \left( P _ { r } \| P _ { g } \right) KL(Pg∥Pr)−2JS(Pr∥Pg) (公式11)
这个等价最小化目标存在两个严重的问题。
第一是它同时要最小化生成分布与真实分布的KL散度,却又要最大化两者的JS散度,一个要拉近,一个却要推远!这在直观上非常荒谬,在数值上则会导致梯度不稳定,这是后面那个JS散度项的毛病。
第二,即便是前面那个正常的KL散度项也有毛病。因为KL散度不是一个对称的衡量, K L ( P g ∥ P r ) K L \left( P _ { g } \| P _ { r } \right) KL(Pg∥Pr)与 K L ( P r ∥ P g ) K L \left( P_{ r } \| P _ { g } \right) KL(Pr∥Pg)是有差别的。以前者为例:
- 当 P g ( x ) → 0 P _ { g } ( x ) \rightarrow 0 Pg(x)→0而 P r ( x ) → 1 P _ { r } ( x ) \rightarrow 1 Pr(x)→1时, P g ( x ) log P g ( x ) P r ( x ) → 0 P _ { g } ( x ) \log \frac { P _ { g } ( x ) } { P _ { r } ( x ) } \rightarrow 0 Pg(x)logPr(x)Pg(x)→0,对 K L ( P g ∥ P r ) K L \left( P _ { g } \| P _ { r } \right) KL(Pg∥Pr)贡献趋近于0
- 当 P g ( x ) → 1 P _ { g } ( x ) \rightarrow 1 Pg(x)→1而 P r ( x ) → 0 P _ { r } ( x ) \rightarrow 0 Pr(x)→0时, P g ( x ) log P g ( x ) P r ( x ) → + ∞ P _ { g } ( x ) \log \frac { P _ { g } ( x ) } { P _ { r } ( x ) } \rightarrow + \infty Pg(x)logPr(x)Pg(x)→+∞, 对 K L ( P g ∥ P r ) K L \left( P _ { g } \| P _ { r } \right) KL(Pg∥Pr)贡献趋于无穷
换言之, K L ( P g ∥ P r ) K L \left( P _ { g } \| P _ { r } \right) KL(Pg∥Pr)对于上面俩种错误的惩罚是不一样的,第一种错误对应的是“生成器没能生成真实的样本”,惩罚微小;第二种错误对应的是“生成器生成了不真实的样本”,惩罚巨大。第一种错误对应的是缺乏多样性,第二种错误对应的是缺乏准确性。这一放一打之下,生成器宁可多生成一些重复但是很“安全”的样本,也不愿意去生成多样性的样本,因为那样一不小心就会产生第二种错误,得不偿失。这种现象就是大家常说的collapse mode。
第二部分小结:在原始GAN的(近似)最优判别器下,第一种生成器loss面临梯度消失问题,第二种生成器loss面临优化目标荒谬、梯度不稳定、对多样性与准确性惩罚不平衡导致mode collapse这几个问题。
实验辅证如下:
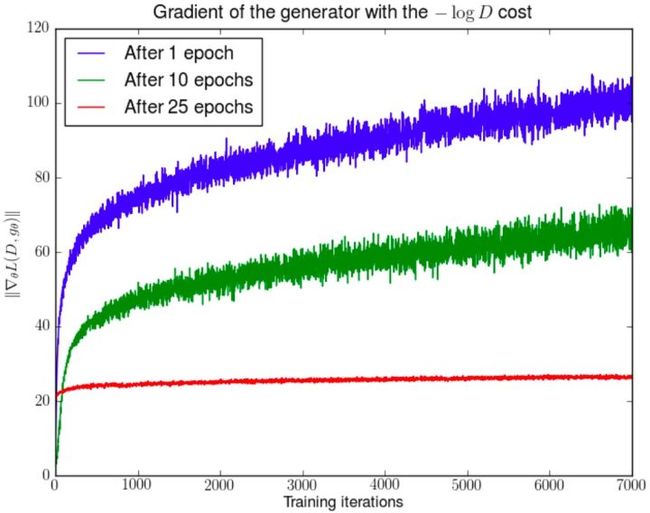
WGAN前作Figure 3。先分别将DCGAN训练1,20,25个epoch,然后固定生成器不动,判别器重新随机初始化从头开始训练,对于第二种形式的生成器loss产生的梯度可以打印出其尺度的变化曲线,可以看到随着判别器的训练,蓝色和绿色曲线中生成器的梯度迅速增长,说明梯度不稳定,红线对应的是DCGAN相对收敛的状态,梯度才比较稳定。
第三部分:WGAN之前的一个过渡解决方案
原始GAN问题的根源可以归结为两点,一是等价优化的距离衡量(KL散度、JS散度)不合理,二是生成器随机初始化后的生成分布很难与真实分布有不可忽略的重叠。
WGAN前作其实已经针对第二点提出了一个解决方案,就是对生成样本和真实样本加噪声,直观上说,使得原本的两个低维流形“弥散”到整个高维空间,强行让它们产生不可忽略的重叠。而一旦存在重叠,JS散度就能真正发挥作用,此时如果两个分布越靠近,它们“弥散”出来的部分重叠得越多,JS散度也会越小而不会一直是一个常数,于是(在第一种原始GAN形式下)梯度消失的问题就解决了。在训练过程中,我们可以对所加的噪声进行退火(annealing),慢慢减小其方差,到后面两个低维流形“本体”都已经有重叠时,就算把噪声完全拿掉,JS散度也能照样发挥作用,继续产生有意义的梯度把两个低维流形拉近,直到它们接近完全重合。以上是对原文的直观解释。
在这个解决方案下我们可以放心地把判别器训练到接近最优,不必担心梯度消失的问题。而当判别器最优时,对公式9取反可得判别器的最小loss为
min L D ( P r + ϵ , P g + ϵ ) = − E x ∼ P r + ϵ [ log D ∗ ( x ) ] − E x ∼ P g + ϵ [ log ( 1 − D ∗ ( x ) ) ] = 2 log 2 − 2 J S ( P r + ϵ ∥ P g + ϵ ) \begin{aligned} \min L _ { D } \left( P _ { r + \epsilon } , P _ { g + \epsilon } \right) & = - \mathbb { E } _ { x \sim P _ { r + \epsilon } } \left[ \log D ^ { * } ( x ) \right] - \mathbb { E } _ { x \sim P _ { g + \epsilon } } \left[ \log \left( 1 - D ^ { * } ( x ) \right) \right] \\ & = 2 \log 2 - 2 J S \left( P _ { r + \epsilon } \| P _ { g + \epsilon } \right) \end{aligned} minLD(Pr+ϵ,Pg+ϵ)=−Ex∼Pr+ϵ[logD∗(x)]−Ex∼Pg+ϵ[log(1−D∗(x))]=2log2−2JS(Pr+ϵ∥Pg+ϵ)
其中 P r + ϵ P _ { r + \epsilon } Pr+ϵ和 P g + ϵ P _ { g + \epsilon } Pg+ϵ分别是加噪后的真实分布与生成分布。反过来说,从最优判别器的loss可以反推出当前两个加噪分布的JS散度。两个加噪分布的JS散度可以在某种程度上代表两个原本分布的距离,也就是说可以通过最优判别器的loss反映训练进程!……真的有这样的好事吗?
并没有,因为加噪JS散度的具体数值受到噪声的方差影响,随着噪声的退火,前后的数值就没法比较了,所以它不能成为P_r和P_g距离的本质性衡量。
因为本文的重点是WGAN本身,所以WGAN前作的加噪方案简单介绍到这里,感兴趣的读者可以阅读原文了解更多细节。加噪方案是针对原始GAN问题的第二点根源提出的,解决了训练不稳定的问题,不需要小心平衡判别器训练的火候,可以放心地把判别器训练到接近最优,但是仍然没能够提供一个衡量训练进程的数值指标。但是WGAN本作就从第一点根源出发,用Wasserstein距离代替JS散度,同时完成了稳定训练和进程指标的问题!
第四部分:Wasserstein距离的优越性质
Wasserstein距离又叫Earth-Mover(EM)距离,定义如下:
W ( P r , P g ) = inf γ ∼ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] W \left( P _ { r } , P _ { g } \right) = \inf _ { \gamma \sim \Pi \left( P _ { r } , P _ { g } \right) } \mathbb { E } _ { ( x , y ) \sim \gamma } [ \| x - y \| ] W(Pr,Pg)=infγ∼Π(Pr,Pg)E(x,y)∼γ[∥x−y∥] (公式12)
解释如下: Π ( P r , P g ) \Pi \left( P _ { r } , P _ { g } \right) Π(Pr,Pg) 是 P r P_{r} Pr和 P g P_{g} Pg组合起来的所有可能的联合分布的集合,反过来说, Π ( P r , P g ) \Pi \left( P _ { r } , P _ { g } \right) Π(Pr,Pg)中每个分布的边缘分布都是 P r P_{r} Pr和 P g P_{g} Pg。对于每一个可能的联合分布 γ \gamma γ而言,可以从中采样 ( x , y ) ∼ γ ( x , y ) \sim \gamma (x,y)∼γ得到一个真是样本x和一个生成样本y,并计算出这对样本的距离 ∣ ∣ x − y ∣ ∣ | | x - y | | ∣∣x−y∣∣,所以可以计算该联合分布 γ \gamma γ下样本对距离的期望值 E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \mathbb { E } _ { ( x , y ) \sim \gamma } [ \| x - y \| ] E(x,y)∼γ[∥x−y∥]。在所有可能的联合分布中能够对这个期望值取到的下界 inf γ ∼ Π ( P r , P g ) E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \inf _ { \gamma \sim \Pi \left( P _ { r } , P _ { g } \right) } \mathbb { E } _ { ( x , y ) \sim \gamma } [ \| x - y \| ] infγ∼Π(Pr,Pg)E(x,y)∼γ[∥x−y∥],就定义为Wasserstein距离。
直观上可以把 E ( x , y ) ∼ γ [ ∥ x − y ∥ ] \mathbb { E } _ { ( x , y ) \sim \gamma } [ \| x - y \| ] E(x,y)∼γ[∥x−y∥]理解为在 γ \gamma γ这个“路径规划下”把 P g P_{g} Pg这堆"沙土"挪到 P r P_{r} Pr”位置“上所需的”消耗“, 而 W ( P r , P g ) W(P_{r},P_{g}) W(Pr,Pg)就是”最优路径规划“下的”最小消耗“,所以才叫Earth-Mover(推土机)距离。
Wasserstein距离相比KL散度、JS散度的优越性在于,即便两个分布没有重叠,Wasserstein距离仍然能够反映它们的远近。
WGAN本作通过简单的例子展示了这一点。考虑如下二维空间中的两个分布 P 1 P_{1} P1和 P 2 P_{2} P2, P 1 P_{1} P1在线段AB上均匀分布, P 2 P_{2} P2在线段CD上均匀分布,通过控制参数 θ \theta θ可以控制着两个分布的距离远近。

此时容易得到(读者可自行验证)
K L ( P 1 ∥ P 2 ) = K L ( P 1 ∥ P 2 ) = { + ∞ if θ ≠ 0 0 if θ = 0 K L \left( P _ { 1 } \| P _ { 2 } \right) = K L \left( P _ { 1 } \| P _ { 2 } \right) = \left\{ \begin{array} { l l } { + \infty } & { \text { if } \theta \neq 0 } \\ { 0 } & { \text { if } \theta = 0 } \end{array} \right. KL(P1∥P2)=KL(P1∥P2)={+∞0 if θ̸=0 if θ=0 (突变)
J S ( P 1 ∥ P 2 ) = { log 2 if θ ≠ 0 0 if θ − 0 J S \left( P _ { 1 } \| P _ { 2 } \right) = \left\{ \begin{array} { l l } { \log 2 } & { \text { if } \theta \neq 0 } \\ { 0 } & { \text { if } \theta - 0 } \end{array} \right. JS(P1∥P2)={log20 if θ̸=0 if θ−0(突变)
W ( P 0 , P 1 ) = ∣ θ ∣ W \left( P _ { 0 } , P _ { 1 } \right) = | \theta | W(P0,P1)=∣θ∣(平滑)
KL散度和JS散度是突变的,要么最大要么最小,Wasserstein距离却是平滑的,如果我们要用梯度下降法优化 θ \theta θ这个参数,前两者根本提供不了梯度,Wasserstein距离却可以。类似地,在高维空间中如果两个分布不重叠或者重叠部分可忽略,则KL和JS既反映不了远近,也提供不了梯度,但是Wasserstein却可以提供有意义的梯度。
第五部分:从Wasserstein距离到WGAN
既然Wasserstein距离有如此优越的性质,如果我们能够把它定义为生成器的loss,不就可以产生有意义的梯度来更新生成器,使得生成分布被拉向真实分布吗?
因为Wasserstein距离定义(公式12)中的 inf γ ∼ Π ( P r , P g ) \inf _ { \gamma \sim \Pi \left( P _ { r } , P _ { g } \right) } infγ∼Π(Pr,Pg)没法直接求解,但是作者用了一个已有的定理把它变换为如下形式:
W ( P r , P g ) = 1 K sup ∥ f ∥ L ≤ K E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] W \left( P _ { r } , P _ { g } \right) = \frac { 1 } { K } \sup _ { \| f \| _ { L } \leq K } \mathbb { E } _ { x \sim P _ { r } } [ f ( x ) ] - \mathbb { E } _ { x \sim P _ { g } } [ f ( x ) ] W(Pr,Pg)=K1sup∥f∥L≤KEx∼Pr[f(x)]−Ex∼Pg[f(x)] (公式13)
证明过程被作者丢到论文附录中了,我们也姑且不管,先看看上式究竟说了什么。
首先需要介绍一个概念——Lipschitz连续。它其实就是在一个连续函数f上面额外施加了一个限制,要求存在一个常数 K ≥ 0 K\geq 0 K≥0使得定义域内的任意两个元素 x 1 x_{1} x1和 x 2 x_{2} x2都满足
∣ f ( x 1 ) − f ( x 2 ) ∣ ≤ K ∣ x 1 − x 2 ∣ \left| f \left( x _ { 1 } \right) - f \left( x _ { 2 } \right) \right| \leq K \left| x _ { 1 } - x _ { 2 } \right| ∣f(x1)−f(x2)∣≤K∣x1−x2∣
简单理解,比如说 f f f的定义域是实数集合,那上面的要求就等价于f的导函数绝对值不超过 K K K。再比如说 log ( x ) \log (x) log(x)就不是Lipschitz连续,因为它的导函数没有上界。Lipschitz连续条件限制了一个连续函数的最大局部变动幅度。
-----这部分完全看不懂-----
公式13的意思就是在要求函数f的Lipschitz常数 ∣ ∣ f ∣ ∣ L ||f||_L ∣∣f∣∣L不超过K的条件下,对所有可能满足条件的f取到 E x ∼ P r [ f ( x ) ] − E x ∼ P g [ f ( x ) ] \mathbb{E}_{x \sim P_r} [f(x)] - \mathbb{E}_{x \sim P_g} [f(x)] Ex∼Pr[f(x)]−Ex∼Pg[f(x)]的上界,然后再除以K。特别地,我们可以用一组参数w来定义一系列可能的函数f_w,此时求解公式13可以近似变成求解如下形式
K ⋅ W ( P r , P g ) ≈ max w : ∣ f w ∣ L ≤ K E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] K \cdot W \left( P _ { r } , P _ { g } \right) \approx \max _ { w : \left| f _ { w } \right| L \leq K } \mathbb { E } _ { x \sim P _ { r } } \left[ f _ { w } ( x ) \right] - \mathbb { E } _ { x \sim P _ { g } } \left[ f _ { w } ( x ) \right] K⋅W(Pr,Pg)≈maxw:∣fw∣L≤KEx∼Pr[fw(x)]−Ex∼Pg[fw(x)] (公式14)
再用上我们搞深度学习的人最熟悉的那一套,不就可以把f用一个带参数w的神经网络来表示嘛!由于神经网络的拟合能力足够强大,我们有理由相信,这样定义出来的一系列 f w f_w fw虽然无法囊括所有可能,但是也足以高度近似公式13要求的那个 s u p ∣ ∣ f ∣ ∣ L ≤ K sup_{||f||_L \leq K} sup∣∣f∣∣L≤K 了。
最后,还不能忘了满足公式14中 ∣ ∣ f w ∣ ∣ L ≤ K ||f_w||_L \leq K ∣∣fw∣∣L≤K这个限制。我们其实不关心具体的K是多少,只要它不是正无穷就行,因为它只是会使得梯度变大K倍,并不会影响梯度的方向。所以作者采取了一个非常简单的做法,就是限制神经网络 f θ f_\theta fθ的所有参数w_i的不超过某个范围[-c, c],比如 w i ∈ [ − 0.01 , 0.01 ] w_i \in [- 0.01, 0.01] wi∈[−0.01,0.01],此时关于输入样本x的导数 ∂ f w ∂ x \frac{\partial f_w}{\partial x} ∂x∂fw也不会超过某个范围,所以一定存在某个不知道的常数K使得f_w的局部变动幅度不会超过它,Lipschitz连续条件得以满足。具体在算法实现中,只需要每次更新完w后把它clip回这个范围就可以了。
-------------------
到此为止,我们可以构造一个含参数w、最后一层不是非线性激活层的判别器网络f_w,在限制w不超过某个范围的条件下,使得
L = E x ∼ P r [ f w ( x ) ] − E x ∼ P g [ f w ( x ) ] L = \mathbb { E } _ { x \sim P _ { r } } \left[ f _ { w } ( x ) \right] - \mathbb { E } _ { x \sim P _ { g } } \left[ f _ { w } ( x ) \right] L=Ex∼Pr[fw(x)]−Ex∼Pg[fw(x)] (公式15)
尽可能取到最大,此时L就会近似真实分布与生成分布之间的Wasserstein距离(忽略常数倍数K)。注意原始GAN的判别器做的是真假二分类任务,所以最后一层是sigmoid,但是现在WGAN中的判别器f_w做的是近似拟合Wasserstein距离,属于回归任务,所以要把最后一层的sigmoid拿掉。
接下来生成器要近似地最小化Wasserstein距离,可以最小化L,由于Wasserstein距离的优良性质,我们不需要担心生成器梯度消失的问题。再考虑到L的第一项与生成器无关,就得到了WGAN的两个loss。
− E x ∼ P g [ f w ( x ) ] - \mathbb { E } _ { x \sim P _ { g } } \left[ f _ { w } ( x ) \right] −Ex∼Pg[fw(x)] (公式16,WGAN生成器loss函数)
E x ∼ P g [ f w ( x ) ] − E x ∼ P r [ f w ( x ) ] \mathbb { E } _ { x \sim P _ { g } } \left[ f _ { w } ( x ) \right] - \mathbb { E } _ { x \sim P _ { r } } \left[ f _ { w } ( x ) \right] Ex∼Pg[fw(x)]−Ex∼Pr[fw(x)] (公式17,WGAN判别器loss函数)
公式15是公式17的反,可以指示训练进程,其数值越小,表示真实分布与生成分布的Wasserstein距离越小,GAN训练得越好。
上文说过,WGAN与原始GAN第一种形式相比,只改了四点:
- 判别器最后一层去掉sigmoid
- 生成器和判别器的loss不取log
- 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
- 不要用基于动量的优化算法(包括momentum和Adam),推荐RMSProp,SGD也行
前三点都是从理论分析中得到的,已经介绍完毕;第四点却是作者从实验中发现的,属于trick,相对比较“玄”。作者发现如果使用Adam,判别器的loss有时候会崩掉,当它崩掉时,Adam给出的更新方向与梯度方向夹角的cos值就变成负数,更新方向与梯度方向南辕北辙,这意味着判别器的loss梯度是不稳定的,所以不适合用Adam这类基于动量的优化算法。作者改用RMSProp之后,问题就解决了,因为RMSProp适合梯度不稳定的情况。
对WGAN作者做了不少实验验证,本文只提比较重要的三点:
- 判别器所近似的Wasserstein距离与生成器的生成图片质量高度相关;
- WGAN如果用类似DCGAN架构,生成图片的效果与DCGAN差不多,但是厉害的地方在于WGAN不用DCGAN各种特殊的架构设计也能做到不错的效果,比如如果大家一起拿掉Batch Normalization的话,DCGAN就崩了;如果WGAN和原始GAN都使用多层全连接网络(MLP),不用CNN,WGAN质量会变差些,但是原始GAN不仅质量变得更差,而且还出现了collapse mode,即多样性不足。
- 在所有WGAN的实验中未观察到collapse mode,作者也只说应该是解决了。
第六部分:总结
WGAN前作分析了Ian Goodfellow提出的原始GAN两种形式各自的问题,第一种形式等价在最优判别器下等价于最小化生成分布与真实分布之间的JS散度,由于随机生成分布很难与真实分布有不可忽略的重叠以及JS散度的突变特性,使得生成器面临梯度消失的问题;第二种形式在最优判别器下等价于既要最小化生成分布与真实分布直接的KL散度,又要最大化其JS散度,相互矛盾,导致梯度不稳定,而且KL散度的不对称性使得生成器宁可丧失多样性也不愿丧失准确性,导致collapse mode现象。
WGAN前作针对分布重叠问题提出了一个过渡解决方案,通过对生成样本和真实样本加噪声使得两个分布产生重叠,理论上可以解决训练不稳定的问题,可以放心训练判别器到接近最优,但是未能提供一个指示训练进程的可靠指标,也未做实验验证。
WGAN本作引入了Wasserstein距离,由于它相对KL散度与JS散度具有优越的平滑特性,理论上可以解决梯度消失问题。接着通过数学变换将Wasserstein距离写成可求解的形式,利用一个参数数值范围受限的判别器神经网络来最大化这个形式,就可以近似Wasserstein距离。在此近似最优判别器下优化生成器使得Wasserstein距离缩小,就能有效拉近生成分布与真实分布。WGAN既解决了训练不稳定的问题,也提供了一个可靠的训练进程指标,而且该指标确实与生成样本的质量高度相关。作者对WGAN进行了实验验证。
转自:https://zhuanlan.zhihu.com/p/25071913
