递推最小二乘法RLS的轮胎侧偏刚度估计(原书缺失代码已补全)

目录

1 参数辨识

1.1 最小二乘法

1.2 递推最小二乘法 RLS

1.3 具有遗忘因子 λ 的递推最小二乘法

2 轮胎线性侧偏刚度估计

2.1 RLS 算法分析

2.2 联合仿真平台的设计

carsim 设置车辆参数

 carsim 设置工况

carsim 设置 IO 模块

Simulink 搭建

2.3 MATLAB 代码分析

主函数框架

初始化函数

mdlOutputs()：变量定义

Carsim 数据传输、预测侧偏角 α 、求解侧偏刚度 Cα

Carsim 数据传输子函数

前轮侧偏刚度估计（RLS主体，原书代码缺失部分）

后轮侧偏刚度估计（RLS主体）

2.4 仿真结果分析

侧偏刚度 Cf、Cr 

侧偏角对比（实际 VS 预测）

车轮横向摩擦力

车轮侧向力误差

误差方差：Pk 

车辆运动状态

Carsim 仿真动画

结论

---

1 参数辨识

背景知识补充。

1.1 最小二乘法

问题描述：

最小二乘法数学模型

先给出未知参数 θ 求解公式：

最小二乘法公式

 推导过程： 

最小二乘法公式证明

缺点：1、需要大量的历史数据，导致占用存储。

           2、无法实时更新。

1.2 递推最小二乘法 RLS

问题描述：如果得到一组新的输入输出数据，怎样利用旧估计，完成新估计，即避免重复使用历史输入输出数据，而一步得到最新估计。

递推公式：

RLS 估计公式

给定初值

 公式证明

1.3 具有遗忘因子 λ 的递推最小二乘法

问题描述

RLS 存在的缺点

 遗忘因子 λ 的加入 

加入遗忘因子的RLS

 递推公式：

具有遗忘因子的递推最小二乘法递推公式

2 轮胎线性侧偏刚度估计

基于车辆动力学模型进行模型预测控制需要用到车辆的状态信息、惯性参数、参考道路信息以及轮胎线性侧偏刚度等。其中，车辆状态信息包括纵向速度、侧向速度、前轮偏角等，车辆惯性参数包括车身质量、车体转动惯量、质心到前后轴的距离位置等，参考道路信息包括路面倾角、道路曲率等。

轮胎线性侧偏刚度是对车辆模型进行线性化的重要参数，反映了车辆在轮胎线性区域内的操作稳定性，而且随行驶工况、路面条件的不同，此参数发生变化。因此对轮胎线性侧偏刚度进行实时估计可以提高无人驾驶车辆对不同附着系数路面的适应性。下面根据车辆的状态信息和惯性参数的历史数据，采用递推最小二乘法估计轮胎的线性侧偏刚度。

2.1 RLS 算法分析

递推最小二乘法公式（这部分可以不看）

公式（5.24）说明（可以不看）：

2.2 联合仿真平台的设计

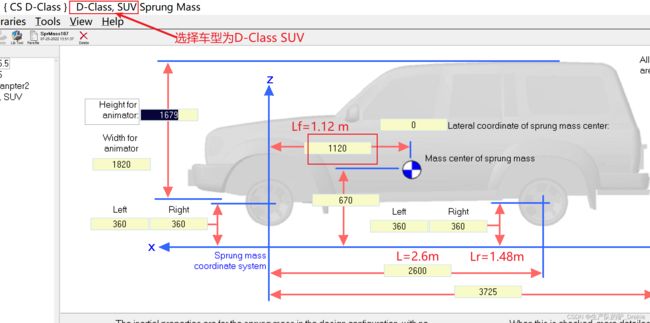
carsim 设置车辆参数

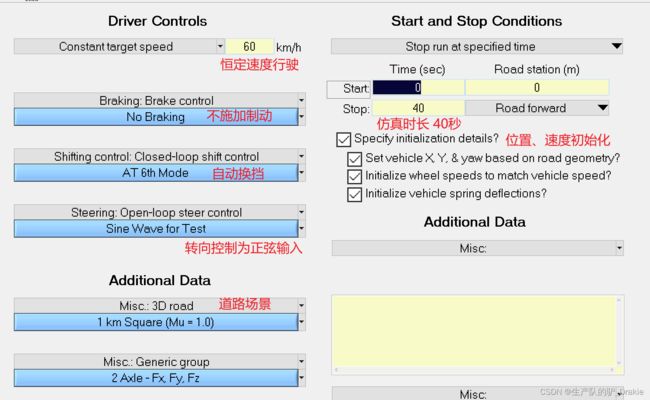
 carsim 设置工况

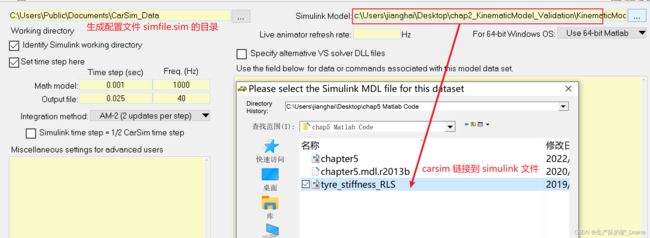
carsim 设置 IO 模块

求解器设置：

 输出变量设置（共13个），添加顺序与 matlab 中对变量 u 的访问顺序保持一致。

修正 7、8 顺序：

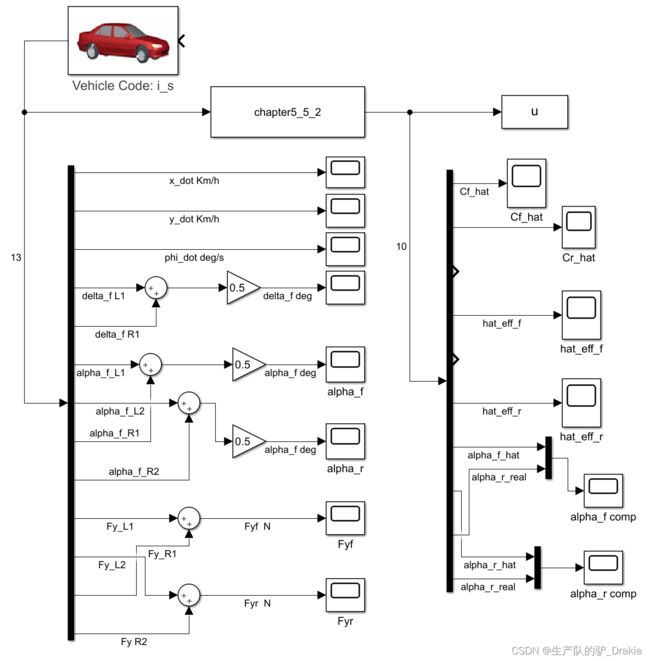
Simulink 搭建

注意事项：轮胎侧偏角为左右轮胎的平均侧偏角，需要乘0.5，轮胎纵向力为左右轮胎的合成，不需要乘0.5。

2.3 MATLAB 代码分析

主函数框架

function [sys,x0,str,ts] =chapter5_5_2(t,x,u,flag)
    switch flag,
        case 0
            [sys,x0,str,ts] = mdlInitializeSizes;
        case 2
            sys = mdlUpdates(t,x,u);
        case 3
            sys = mdlOutputs(t,x,u);
        case {1,4,9}
            sys = [];            
        otherwise
            error(['unhandled flag = ',num2str(flag)]);
    end
end

初始化函数

function [sys,x0,str,ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates  = 0;
sizes.NumDiscStates  = 6; 
sizes.NumOutputs     = 10; % 10 个输出
sizes.NumInputs      = 13; % 13 个输入（来自 carsim）
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = zeros(sizes.NumDiscStates,1);
str = [];
ts  = [0.05 0];
    global InitialGapflag; 
    InitialGapflag = 0;
    global VehicleParams;
    VehicleParams.Lf  = 1.12; % 前轴距
    VehicleParams.Lr  = 1.48; % 后轴距
    [y, c] = func_RLSEstimation_Cf('initial', 0.95, 1, 10); % λ=0.95，θ数目为1，Pk 初值为 10
    [y, c] = func_RLSEstimation_Cr('initial', 0.95, 1, 10);
end

mdlOutputs()：变量定义

function sys = mdlOutputs(t,x,u)
global InitialGapflag;
global VehicleParams;
Cf_Hat      = 0; % Cf 估计值，输出可视
Cr_Hat      = 0;
Pk_f        = 0; % Pk 协方差，输出可视
Pk_r        = 0;
Fyf_err     = 0; % Fy 误差值，输出可视
Fyr_err     = 0;  
alpha_f_Hat    = 0;
alpha_r_Hat    = 0; 
alpha_f_Direct = 0;
alpha_r_Direct = 0;
if InitialGapflag < 3 % 防止carsim 传输的前几个值为空
    InitialGapflag  = InitialGapflag + 1;

Carsim 数据传输、预测侧偏角 α 、求解侧偏刚度 Cα

else 
    InitialGapflag  = InitialGapflag + 1;
    [Carsim_export] = func_CarsimData_Parse(u);   
    Vx              = Carsim_export.x_dot; 
    Vy              = Carsim_export.y_dot; 
    yawrate         = Carsim_export.phi_dot; % rad/s
    delta_f         = Carsim_export.delta_f; % 前轮转角 rad
    Fyf_Direct      = Carsim_export.Fyf;
    Fyr_Direct      = Carsim_export.Fyr;   
    alpha_f_Direct  = Carsim_export.alphaf; % 来自 carsim 的前轮侧偏角
    alpha_r_Direct  = Carsim_export.alphar; % 来自 carsim 的后轮侧偏角
    % 前轮
    alpha_f_Hat = (Vy + yawrate * VehicleParams.Lf)/Vx - delta_f;
    [Fyf_Hat, Cf_Hat, Pk_f] = func_RLSEstimation_Cf(alpha_f_Hat, Fyf_Direct);
    Fyf_err = Fyf_Hat - Fyf_Direct; % 横向摩擦力的误差比较
    % 后轮
    alpha_r_Hat = (Vy - yawrate * VehicleParams.Lr)/Vx;
    [Fyr_Hat, Cr_Hat, Pk_r] = func_RLSEstimation_Cr(alpha_r_Hat, Fyr_Direct);
    Fyr_err = Fyr_Hat - Fyr_Direct;
end
sys = [Cf_Hat; Cr_Hat; Pk_f; Fyf_err; Pk_r; Fyr_err; alpha_f_Hat; alpha_r_Hat; alpha_f_Direct; alpha_r_Direct];
end

其中 αf 和 αr 的求解是通过如下公式：

侧偏角 公式

Carsim 数据传输子函数

function [Sparsed_Carsim_Data] = func_CarsimData_Parse(CarsimData)     
    Sparsed_Carsim_Data.x_dot   = CarsimData(1)/3.6; %Unit:km/h-->m/s，保留1位小数  
    Sparsed_Carsim_Data.y_dot   = CarsimData(2)/3.6; %Unit:km/h-->m/s，保留1位小数   
    Sparsed_Carsim_Data.phi_dot = (round(10*CarsimData(3))/10)*pi/180; %Unit：deg/s-->rad/s，保留1位小数      
    Sparsed_Carsim_Data.delta_f     = (round(10*0.5*(CarsimData(4)+ CarsimData(5)))/10)*pi/180; % 左、右前轮转角 % deg-->rad，对应carsim Steer_L1 R1
    Sparsed_Carsim_Data.alphaf     = (round(10*0.5 * (CarsimData(6)+ CarsimData(8)))/10)*pi/180; % 左、右前轮侧偏角 对应 carsim Alpha_L1 R1 deg-->rad，保留1位小数   
    Sparsed_Carsim_Data.alphar     = (round(10*0.5 * (CarsimData(7)+ CarsimData(9)))/10)*pi/180; % 左、右后轮侧偏角 对应 carsim Alpha_L2 R2 deg-->rad，保留1位小数  
    Fy_l1      = round(10*CarsimData(10))/10; %Unit:N，保留1位小数  
    Fy_l2      = round(10*CarsimData(11))/10; %Unit:N，保留1位小数  
    Fy_r1      = round(10*CarsimData(12))/10; %Unit:N，保留1位小数  
    Fy_r2      = round(10*CarsimData(13))/10; %Unit:N，保留1位小数  
    Sparsed_Carsim_Data.Fyf  = Fy_l1 + Fy_r1;
    Sparsed_Carsim_Data.Fyr  = Fy_l2 + Fy_r2;
end

前轮侧偏刚度估计（RLS主体，原书代码缺失部分）

回顾具有遗忘因子的递推最小二乘公式

具有 λ 的 RLS 的递推公式

 更新 K(k+1)、P(k+1)，求解 θ(k+1)

function[Fyf_hat, Cf_hat,Pkf]  = func_RLSEstimation_Cf(alpha_f_hat,Fyf_direct, Param_Num, Pkf_init)
    % Fyf_hat 是 Fy 估算值
    % Cf_hat 是前轮侧偏刚度 Cf 的估算值
    % Pkf 是 Pk
    % alpha_f_hat  ：已知量（来自模型预测）
    % Fyf_direct   ：已知量（来自 Carsim ）
    % Param_Num    ：待估计的参数数量，这里只有 Cf，所以 Param_Num =1
    % Pkf_init     ：Pk 初始值
    persistent alpha_f Cf lambda_f Pk_f % 定义静态变量，在Simulink整个运行期间都有值
    %% 初始化：静态变量赋值
    if (ischar(alpha_f_hat) && strcmp(alpha_f_hat,'initial')) 
        alpha_f = zeros(Param_Num,1);   % 定义 alpha_f 的维度为1
        Cf = zeros(Param_Num,1);        % 定义 Cf      的维度为 1
        lambda_f = Fyf_direct;             % λ= 0.95，Fy_direct 作为形参传递 λ
        Pk_f = Pkf_init * eye(Param_Num);  % Pk = 10,初始值
        Fyf_hat = 0; % initial 阶段返回值为0
        Cf_hat = 0;
    else
    %% 带λ的 RLS算法主体:
        alpha_f= alpha_f_hat; % 初值选取，Pk 已经在initial 阶段赋了初值
        % RLS 的3个公式
        Kf = Pk_f * alpha_f / (lambda_f + alpha_f' * Pk_f * alpha_f);
        Pkf_next = (Pk_f - Kf * alpha_f' * Pk_f) / lambda_f;
        Cf = Cf + Kf * (Fyf_direct - alpha_f' * Cf);
        Pk_f = Pkf_next; % Pk 更新，作为下一时刻初值
        % 输出变量
        Fyf_hat   = alpha_f'* Cf;
        Cf_hat = Cf; % 最终值
        Pkf = Pk_f;
    end
end

后轮侧偏刚度估计（RLS主体）

function[Fyr_hat, Cr_hat,Pkr]  = func_RLSEstimation_Cr(alpha_r_hat,Fyr_direct, Param_Num, Pkr_init)
    persistent alpha_r Cr lambda_r Pk_r
    if (ischar(alpha_r_hat) && strcmp(alpha_r_hat,'initial')) 
        alpha_r = zeros(Param_Num,1);
        Cr = zeros(Param_Num,1);
        lambda_r = Fyr_direct;
        Pk_r = Pkr_init * eye(Param_Num);
        Fyr_hat = 0;
        Cr_hat = 0;
    else
        alpha_r= alpha_r_hat;
        Kr = Pk_r * alpha_r / (lambda_r + alpha_r' * Pk_r * alpha_r);
        Pkr_next = (Pk_r - Kr * alpha_r' * Pk_r) / lambda_r;
        Cr = Cr + Kr * (Fyr_direct - alpha_r' * Cr);
        Pk_r = Pkr_next;
        Fyr_hat   = alpha_r'* Cr;
        Cr_hat = Cr;
        Pkr = Pk_r;
    end
end

2.4 仿真结果分析

侧偏刚度 Cf、Cr 

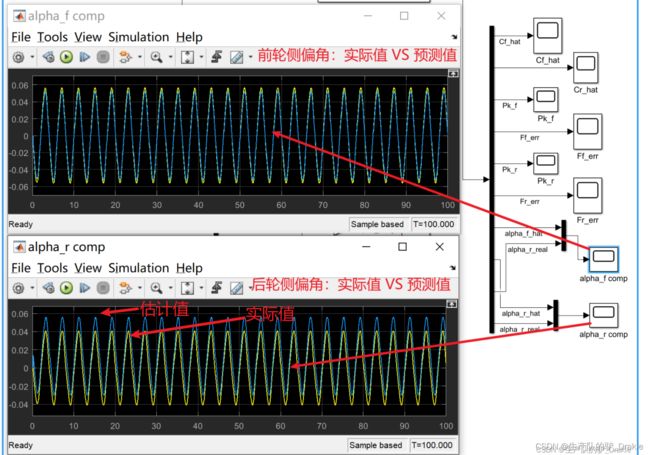
侧偏角对比（实际 VS 预测）

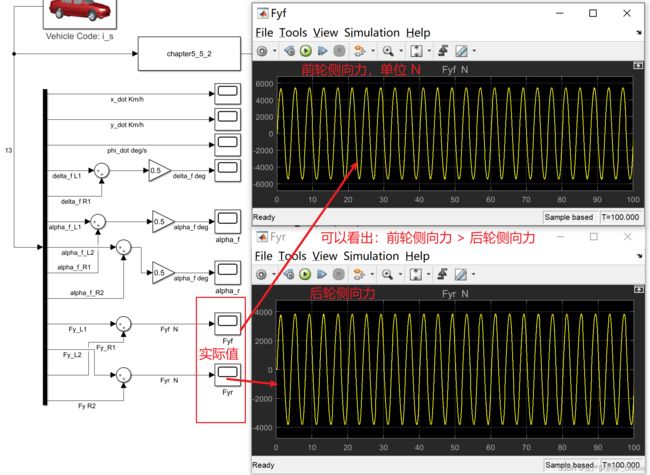
车轮横向摩擦力

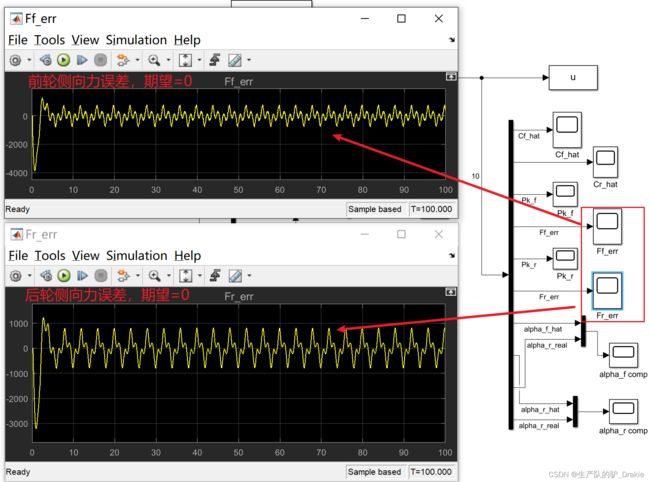
车轮侧向力误差

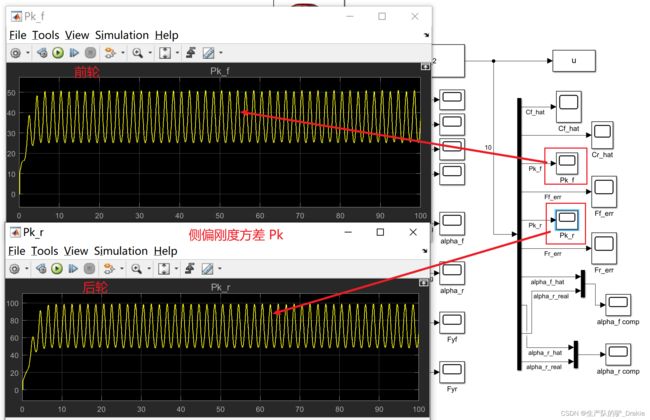
误差方差：Pk 

车辆运动状态

Carsim 仿真动画

结论

从车辆前轮和后轮的侧偏刚度估计结果可以看出，估计值快速地达到收敛状态。

侧向力峰值 Ff = 5000 N

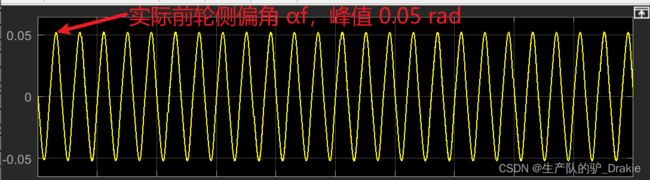
侧偏角峰值 αf = 0.05 rad

侧偏刚度估算值恰好为 5000 / 0.05 ≈ 10000，即为如下值：

 所以本算法能够很好地提供轮胎侧偏刚度估计。另外发现轮胎的侧偏刚度保持在一个恒定值附近波动，因此在车辆动力学中可以被当作固定值处理。