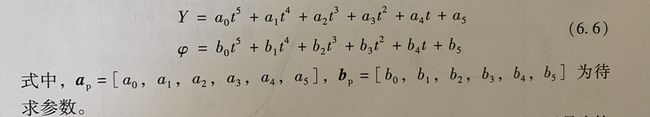带避障功能的MPC局部路径规划+跟踪控制学习笔记
目录
1 轨迹跟踪MPC设计
1.1 非线性模型预测控制算法
1.1.1 非线性MPC概述
1.1.2 基于动力学的车辆点质量模型(非线性、连续)
1.1.3 离散化为预测模型
1.1.4 避障功能函数及MPC目标函数
1.1.5 5次多项式拟合
1.2 代码实现
S 函数框架
初始化子函数
MPC算法子函数
参考路径:全局路径
添加障碍物位置信息
截取 Np 时域内的局部路径作为参考路径
设置待求解未知量 ay 的约束条件
fmincon() 求解 Nc 时域内的最优 ay 序列
根据ay序列及点质量模型,预测推导 Np 时域内的局部路径
polyfit() 拟合 Y_predict 和 φ_predict 的5次多项式、输出系数
子函数:预测状态和未知量 ay 的函数关系
3 MPC 轨迹跟踪控制器
3.1 MPC 算法设计
3.2 代码实现
mdlInitializeSizes()
系统参数、车辆及路况参数设定
来自 Carsim 的状态,及规划层曲线参数的传入
通过polyval() 生成局部参考路径
构建基于 Δu 的 kesi(k+1) 增广系统
构建 PSI THETA GAMMA PHI 矩阵
Q R H E f 矩阵
控制量约束、控制增量约束、输出约束
quadprog() 求解、输出
4 Carsim / Simulink联合仿真
4.1 Carsim 设计
4.3 不同车速跟踪验证
中低速:36 Km/h,跟踪效果良好
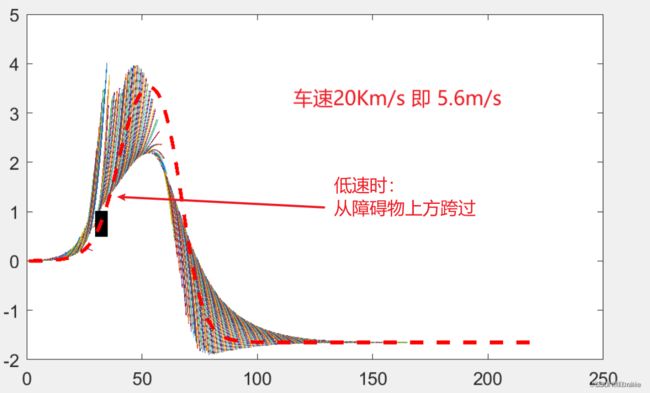
低速:20 Km/h,可以跟踪,效果较差
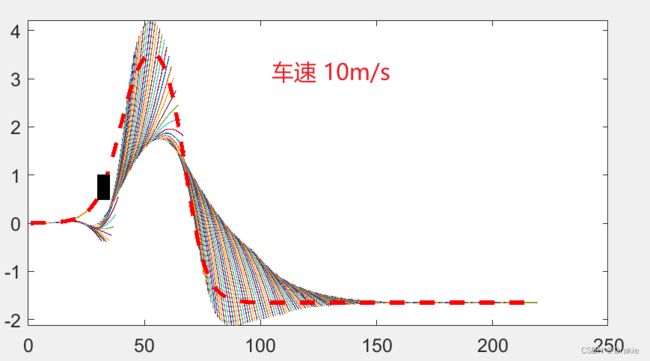
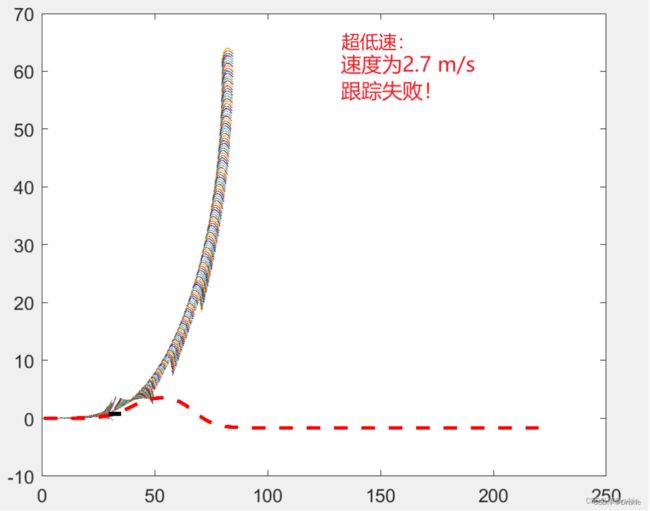
超低速:10 Km/s,跟踪失败
超低速跟踪失败原因分析:
中高速:72 Km/h,跟踪良好
高速:108 Km/h,跟踪良好(不考虑侧倾稳定性)
调整障碍物位置,观察避障效果
避障系数 S 的影响
Carsim 动画效果展示
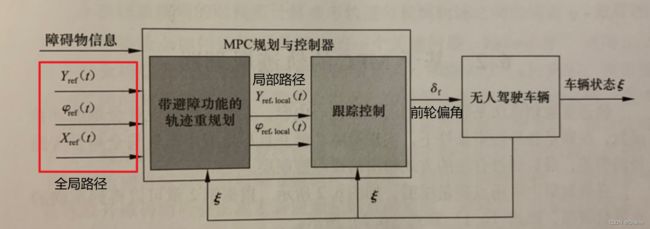
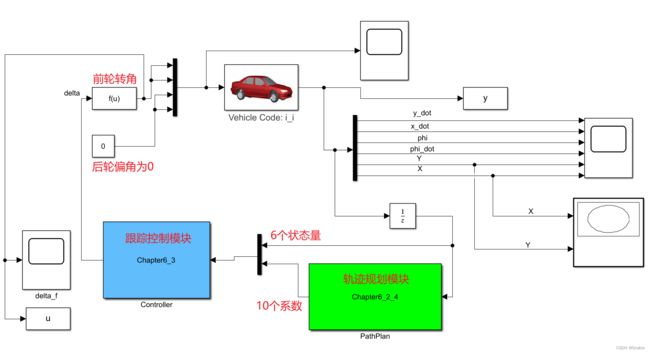
本文介绍无人驾驶车辆结合路径规划层的轨迹跟踪控制器。首先介绍了基于车辆点质量模型的MPC轨迹规划控制器,规划出满足车辆动力学约束并实现避障的可行轨迹;然后 介绍了在车辆动力学模型基础上MPC路径跟踪控制器,并给出了S函数代码,以及利用Simulink/Carsim实现联合仿真。加入局部规划层的轨迹跟踪控制系统主要由轨迹规划模块、跟踪控制模块构成,结构如下:
轨迹规划模块根据全局参考路径、以及来自传感器的障碍物信息,通过非线性MPC算法规划出局部参考路径点,再拟合成5次多项式,并将系数打包发送给跟踪控制模块。
跟踪控制模块接收到来自规划层的局部参考路径5次多项式系数,逆向得出局部路径参考点,从而通过MPC算法设计出最优控制量,即下一时刻的前轮偏角。
1 轨迹跟踪MPC设计
由于规划规划层算法计算量庞大,因此对车辆模型部分使用忽略尺寸信息的点质量模型。另外由于规划层一个周期内可规划出若干个控制周期的路径,因此控制周期比轨迹跟踪的要行,本节选为跟踪控制周期的2倍。
1.1 非线性模型预测控制算法
1.1.1 非线性MPC概述
1.1.2 基于动力学的车辆点质量模型(非线性、连续)
由公式(6.1)看出,轨迹规划器的控制量为横向加速度ay,这是和轨迹跟踪控制器最大的区别。规划器的目的是求解出一组Np时域内的最优横向加速度ay,并根据离散化后的点质量模型,结合车辆当前的状态,预测出未来Np时域内的状态量,即局部路径规划。至于前轮偏角,则是轨迹跟踪控制器的任务。
1.1.3 离散化为预测模型
在非线性模型预测控制中,通过非线性模型,当前的状态量和控制时域内的控制量序列,可以对未来的状态量进行预测。显然这是一个迭代过程,由于控制序列不可知,就需要找到一个显式的迭代方程,对微分方程进行近似求解。在实际工程中,使用较为广泛的数值解法有欧拉法、4阶龙格库塔算法。本节采用较为单步前向欧拉法:
1.1.4 避障功能函数及MPC目标函数
1、避障功能函数:设计的思路是通过障碍物与目标点的距离偏差来调节惩罚函数值的大小,即距离越近,函数值越大。权重系数Sobs增加时会使规划结果趋于保守;而当车辆没有接收到障碍物信息时,权重系数不会对规划结果产生任何影响。当车辆状态测量或者估计存在较大的误差时,可以采用较大的权重系数,但同时也带来了跟踪偏差增加的问题,具体形式如公式(6.4)。
2、目标函数:轨迹规划层的控制目标是尽量减少与全局参考路径的偏差,并且实现对障碍物的避让。对障碍物的避让以惩罚函数的方式实现。具体形式如公式(6.5)
由于规划层的实时性要求比控制层低,点质量模型相对于非线性动力学模型也进行了较大程度的简化,具备更高求解精度的非线模型预测控制算法完全能够满足轨迹规划的要求,而非线性目标函数的采用也能给后续惩罚函数的设计带来便利。因此对公式(6.5)不再线性化,而是直接基于非线性模型求解。
1.1.5 5次多项式拟合
在轨迹规划算法中,将目标函数设定为有限时域内与参考点距离偏差最小,所规划出的轨迹是以预测时域内的离散点给出的。随着预测时域的增加,这些局部参考轨迹点的数量也会增加。直接将这些点输入控制层,占用了过多的控制器输入接口,不利于控制器的规范化设计。另外由于规划层与控制层的控制周期不一致,控制层很难根据离散点的参考轨迹完成轨迹跟踪的任务。
综合上述因素,有必要对轨迹规划算法所规划出的局部参考路径进行处理,实现规划层与控制层的顺利对接。曲线拟合是对离散点的处理的主要方式,由于车辆位置连续要求曲线是连续的,横摆角连续要求曲线是一阶连续的,而加速度约束则要求曲线二阶连续,因此本书选择 5 次多项式作为拟合曲线。
1.2 代码实现
轨迹规划器将 carsim 的 6 个参数 [ y_dot x_dot φ φ_dot Y X ] 输出作为输入,将期望轨迹的拟合多项式系数作为输出,包含 Y 和 φ 各自的 5 个系数,这里输出量为 10 个。
S 函数框架
第一部分为主体的 S-Function,实现了程序整体的框架。通过主函数调用不同的功能子函数,如初始化子函数设置函数模块的输入输出变量、状态变量个数等。
function [sys,x0,str,ts] = MPC_TrajPlanner(t,x,u,flag)
switch flag,
case 0
[sys,x0,str,ts] = mdlInitializeSizes;
case 2
sys = mdlUpdates(t,x,u);
case 3
sys = mdlOutputs(t,x,u);
case {1,4,9}
sys = [];
otherwise
error(['unhandled flag = ',num2str(flag)]);
end初始化子函数
function [sys,x0,str,ts] = mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0; % 连续状态变量的个数
sizes.NumDiscStates = 5; % 离散状态变量的个数
sizes.NumOutputs = 10; % 拟合曲线的10个系数,Y和phi的参考轨迹
sizes.NumInputs = 6; % 输入变量的个数
sizes.DirFeedthrough = 1; % 存在直接贯通
sizes.NumSampleTimes = 1; % 模块的采样次数,至少是一个
sys = simsizes(sizes); % 设置完后赋给sys输出
x0 =[0.001;0.0001;0.0001;0.00001;0.00001;]; % 状态初值
str = [];
ts = [0.1 0]; % [period, offset],轨迹规划的周期为 100ms,是跟踪控制周期的2倍MPC算法子函数
% 算法主体
function sys = mdlOutputs(t,x,u)
tic
Nx=5; % 5个状态量
Np =15; % 预测时域
Nc=2; % 控制时域
%% 输入输出对接
T=0.1; % 采样周期,
y_dot=u(1)/3.6; % 当前时刻横向速度 m/s
x_dot=u(2)/3.6+0.0001; % 当前时刻纵向速度 m/s,加0.0001是为了防止分母为零
phi=u(3)*pi/180; % 当前时刻横摆角,degree 转换为 rad
Y=u(5); % 当前时刻 Y 坐标
X=u(6); % 当前时刻 X 坐标参考路径:全局路径
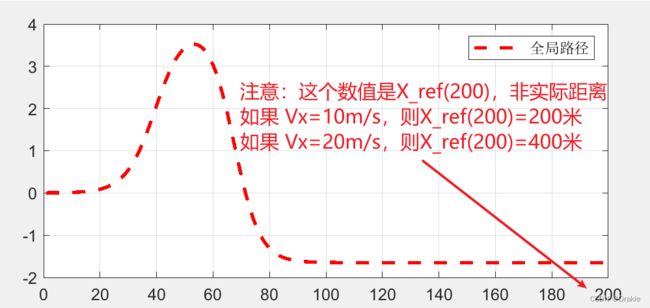
%% 全局路径(双移线)
shape=2.4; % 双移线参数
dx1=25;dx2=21.95; % 双移线参数
dy1=4.05;dy2=5.7; % 双移线参数
Xs1=27.19;Xs2=56.46;% 双移线参数
X_phi=1:1:200; % 速度为10m/s则每个控制周期前进1米;速度为20m/s,则总长为200米
z1=shape/dx1*(X_phi-Xs1)-shape/2;
z2=shape/dx2*(X_phi-Xs2)-shape/2;
Y_ref_global=dy1/2.*(1+tanh(z1))-dy2/2.*(1+tanh(z2));
figure(1);
plot(X_phi, Y_ref_global,'r--','LineWidth',2);
grid;
legend("全局路径");
hold on;图示:
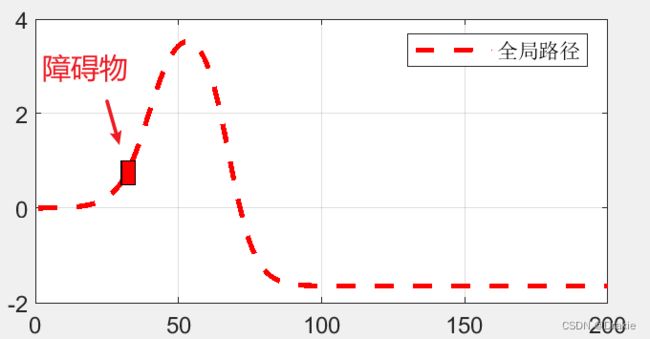
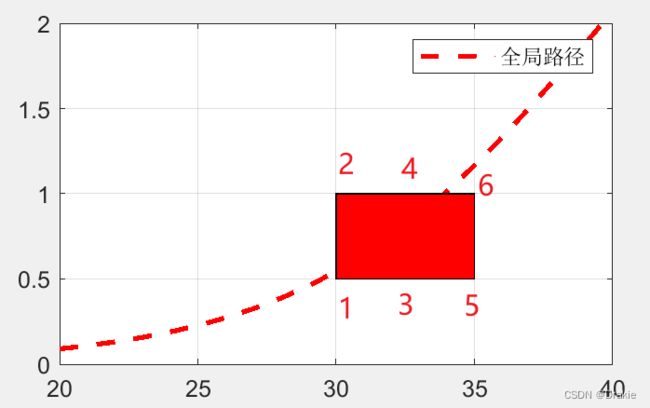
添加障碍物位置信息
%% 障碍物位置
X_obstacle=zeros(Nobs,1);
X_obstacle(1:2)=30; % 障碍物1、2 在X位置 30m 处
X_obstacle(3:4)=35; % 障碍物3、4 在X位置 35m 处
X_obstacle(5:6)=32.5; % 障碍物5、6 在X位置 32.5m 处
Y_obstacle=zeros(Nobs,1);
Y_obstacle(1)=0.5; % 障碍物1 在Y位置 0.5m 处
Y_obstacle(2)=1; % 障碍物2 在Y位置 1m 处
Y_obstacle(3)=0.5; % 障碍物3 在Y位置 0.5m 处
Y_obstacle(4)=1; % 障碍物3 在Y位置 1m 处
Y_obstacle(5)=0.5; % 障碍物3 在Y位置 0.5m 处
Y_obstacle(6)=1; % 障碍物3 在Y位置 1m 处
figure(1);
rectangle('Position',[X_obstacle(1),Y_obstacle(1),5,0.5],'EdgeColor','black', 'FaceColor','red');
hold on;图示 :
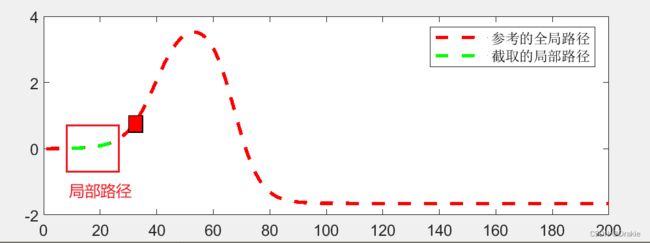
截取 Np 时域内的局部路径作为参考路径
这里的局部路径并不是由MPC规划器求出的最优局部路径,而是 从全局路径上截取的一段Np时域内的局部路径,仅作为参考量 用于求解真正的最优局部路径。
%% 局部路径
State_Initial=zeros(Nx,1);
State_Initial(1,1)=y_dot;
State_Initial(2,1)=x_dot;
State_Initial(3,1)=phi;
State_Initial(4,1)=Y;
State_Initial(5,1)=X;
Yref_local=(Y_ref_global(1,round(State_Initial(5,1))+1:round(State_Initial(5,1))+15))';图示:
设置待求解未知量 ay 的约束条件
这里的约束条件是针对未知量横向加速度的约束。
%% 约束条件 (横向加速度 ay 的约束)
mu=0.4; % 地面摩擦系数
g=9.8; % 重力加速度
lb=zeros(Nc,1); % 约束下限
ub=zeros(Nc,1); % 约束上限
umin = -mu*g; % 来自地面摩擦力
umax = mu*g; %
for i_u=1:Nc
lb(i_u,1)=umin;
ub(i_u,1)=umax;
endfmincon() 求解 Nc 时域内的最优 ay 序列
理想的输出惩罚项 η 应该包含 (Y-Y_ref) 和( φ - φ_ref),这样才能在求解时同时减小与参考轨迹的横向位置误差及横摆角误差。但本节为了简化设计,本节只对横向位置误差(Y-Y_ref)进行约束,即在目标函数中不包含与横摆角 φ_ref 的偏差惩罚项,这种较宽松的惩罚项同样可以达到控制目的,只是小车的实时横摆角 φ(i) 不再跟随参考值 φ_ref。关于建立未知量 ay(i) 和输出量Y_predict(i)的函数关系,需要跳转至子函数My_costfunction() 进行实现。
%% fmincon() 求解每一时刻的最优横向加速度
Q = 100*eye(Np,Np); % QR 调参
R = 20*eye(Nc,Nc);
options = optimset('Algorithm','active-set');
[A,fval,exitflag]=fmincon(@(x)MY_costfunction(x,State_Initial,Np,Nc,Nobs,T,Yref_local,Q,X_obstacle,Y_obstacle),[0;0;],[],[],[],[],lb,ub,[],options);
% A 包含 ay(1)和 ay(2)根据ay序列及点质量模型,预测推导 Np 时域内的局部路径
根据离散化后的非线性点质量模型公式(6.1a),就可以预测未来 Np 时域内的 Y_predict 和 φ_predict,这也是局部路径的含义。这里的 Y_predict 和 φ_predict 就是预测时域内的 Y_ref 和 φ_ref,命名是为了避免和当前时刻参考路径的冲突。
%% 求解局部参考路径
y_dot_predict=zeros(Np,1);
x_dot_predict=zeros(Np,1);
phi_predict=zeros(Np,1);
Y_predict=zeros(Np,1);
X_predict=zeros(Np,1);
for i=1:1:Np
if i < Nc-1
ay(i)=A(1);
y_dot_predict(i,1)=State_Initial(1,1)+T*ay(i);
x_dot_predict(i,1)=State_Initial(2,1);
phi_predict(i,1)=State_Initial(3,1)+T*ay(i)/State_Initial(2,1);
Y_predict(i,1)=State_Initial(4,1)+T*(State_Initial(2,1)*sin(State_Initial(3,1))+State_Initial(1,1)*cos(State_Initial(3,1)));
X_predict(i,1)=State_Initial(5,1)+T*(State_Initial(2,1)*cos(State_Initial(3,1))-State_Initial(1,1)*sin(State_Initial(3,1)));
else
ay(i)=A(2);
y_dot_predict(i,1)=y_dot_predict(i-1,1)+T*ay(i);
x_dot_predict(i,1)=State_Initial(2,1);
phi_predict(i,1)=phi_predict(i-1,1)+T*ay(i)/x_dot_predict(i-1,1);
Y_predict(i,1)=Y_predict(i-1)+T*(State_Initial(2,1)*sin(phi_predict(i-1))+y_dot_predict(i-1)*cos(phi_predict(i-1)));
X_predict(i,1)=X_predict(i-1)+T*(State_Initial(2,1)*cos(phi_predict(i-1))-y_dot_predict(i-1)*sin(phi_predict(i-1)));
end
endpolyfit() 拟合 Y_predict 和 φ_predict 的5次多项式、输出系数
得到未来 Np 时域内的 Y_predict(i) 和 φ_predict(i) 参考值后,分别拟合 Y_predict 与 X 的关系曲线,及 φ_predict 与X 的关系曲线
%% 五次多项式拟合
Paramater_X_Y=polyfit(X_predict,Y_predict,4);
Paramater_X_PHI=polyfit(X_predict,phi_predict,4);
OutPut(1:5)=Paramater_X_Y;
OutPut(6:10)=Paramater_X_PHI;
sys=OutPut;
figure(1);
xx =X_predict(1,1):1:X_predict(Np,1);
yy= Paramater_X_Y(1)*xx.^4+ Paramater_X_Y(2)*xx.^3+ Paramater_X_Y(3)*xx.^2+ Paramater_X_Y(4)*xx+ Paramater_X_Y(5);
plot(xx,yy);
hold on;
toc子函数:预测状态和未知量 ay 的函数关系
function cost = MY_costfunction(x,State_Initial,Np,Nc,Nobs,T,Yref_local,Q,R,X_obstacle,Y_obstacle)
% 这里自变量 x 包括:x(1)、x(2)
%% 状态量初始值
y_dot=State_Initial(1,1);
x_dot=State_Initial(2,1);
phi=State_Initial(3,1);
Y=State_Initial(4,1);
X_start=State_Initial(5,1);
%% 状态量预测
y_dot_predict=zeros(Np,1);
x_dot_predict=zeros(Np,1);
phi_predict=zeros(Np,1);
Y_predict=zeros(Np,1);
X_predict=zeros(Np,1);
J_obst=zeros(Np,1); % i时刻的避障函数
ay=zeros(Np,1);
for i=1:1:Np
if i == Nc-1 % Nc=2
ay(i,1)=x(1); % 待求的 x(1)
y_dot_predict(i,1)=y_dot+T * ay(i,1);
x_dot_predict(i,1)=x_dot;
phi_predict(i,1)=phi+T*ay(i)/x_dot;
Y_predict(i,1)=Y+T*(x_dot*sin(phi)+y_dot*cos(phi));
X_predict(i,1)=X_start+T*(x_dot*cos(phi)-y_dot*sin(phi));
for j=1:1:Nobs % 6 个障碍物的惩罚函数之和,这里速度 Vi恒定,作为系数合并在 Sobs 中
J_obst(i,1)=J_obst(i,1)+1/(((X_predict(i,1))-X_obstacle(j,1))^2+(Y_predict(i,1)-Y_obstacle(j,1))^2+0.000001);
end
else %
ay(i,1)=x(2); % 待求的 x(2)
y_dot_predict(i,1)=y_dot_predict(i-1,1) + T * ay(i,1);
x_dot_predict(i,1)=x_dot;
phi_predict(i,1)=phi_predict(i-1,1)+T * ay(i)/x_dot_predict(i-1,1);
Y_predict(i,1)=Y_predict(i-1) + T * (x_dot*sin(phi_predict(i-1))+y_dot_predict(i-1)*cos(phi_predict(i-1)));
X_predict(i,1)=X_predict(i-1) + T * (x_dot*cos(phi_predict(i-1))-y_dot_predict(i-1)*sin(phi_predict(i-1)));
for p=1:1:Nobs
J_obst(i,1)=J_obst(i,1)+1/(((X_predict(i,1))-X_obstacle(p,1))^2+(Y_predict(i,1)-Y_obstacle(p,1))^2+0.000001);
end
end
Y_error=zeros(Np,1);
Y_error(i,1)=Y_predict(i,1)-Yref_local(i,1);
end
%% 代价函数J
S=100; % 避障函数的权重
cost = Y_error' * Q * Y_error + ay(1:2)' * R * ay(1:2)+ S * sum(J_obst(:));3 MPC 轨迹跟踪控制器
3.1 MPC 算法设计
基于线性时变预测模型的轨迹跟踪控制,算法与双移线轨迹跟踪部分一致,不再赘述。
3.2 代码实现
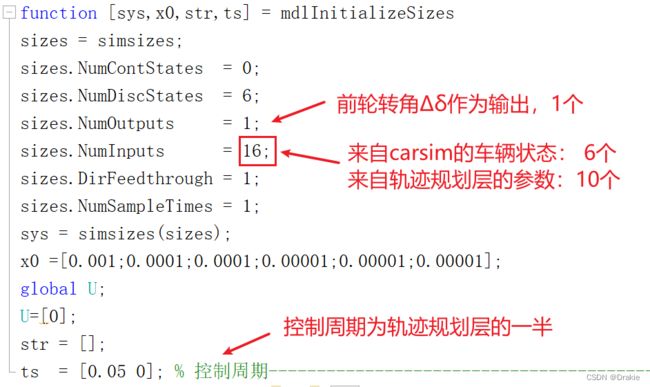
mdlInitializeSizes()
系统参数、车辆及路况参数设定
function sys = mdlOutputs(t,x,u)
%% 系统参数设定
tic % 计时开始
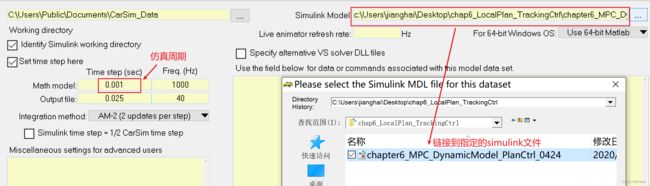
T=0.05; % 控制周期
% 参数定义
Nx=6; % 状态量的个数
Nu=1; % 控制量的个数
Ny=2; % 输出量的个数
Np =15; % 预测步长
Nc=2; % 控制步长
%% 车身及路况参数设定,用于求解雅可比矩阵 a、b,预测模型
Sf=0.2; Sr=0.2; % 前、后轮滑移率,根据路况实时更新
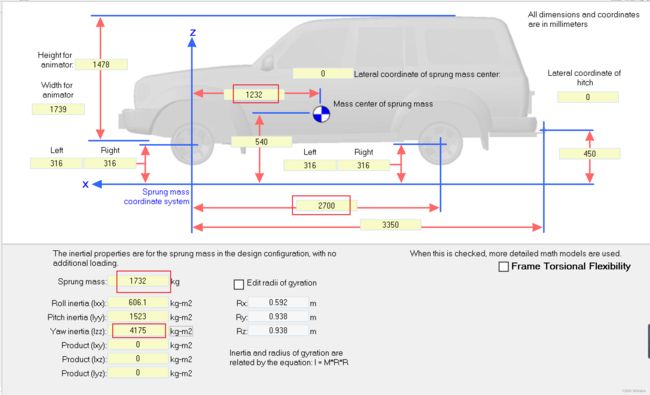
lf=1.232;lr=1.468; % 前、后轮距车辆质心距,车辆固有参数
Ccf=66900;Ccr=62700; % 前、后轮纵向侧偏刚度,车辆固有参数
Clf=66900;Clr=62700; % 前、后轮纵向侧偏刚度,车辆固有参数
m=1723;g=9.8;I=4175; % 车辆质量、重力加速度、绕 Z 轴转动惯量,车辆固有参数来自 Carsim 的状态,及规划层曲线参数的传入
%% 从 Carsim 获取车辆当前状态
y_dot=u(1)/3.6;
x_dot=u(2)/3.6+0.0001;
phi=u(3)*3.141592654/180;
phi_dot=u(4)*3.141592654/180;
Y=u(5);
X=u(6);
%% 从规划层获取 5 次多项式参数
Paramater_X_Y(1,1)=u(7); % Y_ref 的曲线参数
Paramater_X_Y(1,2)=u(8);
Paramater_X_Y(1,3)=u(9);
Paramater_X_Y(1,4)=u(10);
Paramater_X_Y(1,5)=u(11);
Paramater_X_phi(1,1)=u(12); % phi_ref 的曲线参数
Paramater_X_phi(1,2)=u(13);
Paramater_X_phi(1,3)=u(14);
Paramater_X_phi(1,4)=u(15);
Paramater_X_phi(1,5)=u(16);通过polyval() 生成局部参考路径
%% polyval()生成局部参考路径
X_predict=zeros(Np,1); % 预测下一时刻的纵向位置 X
Y_ref=zeros(Np,1); % Np 时域内的参考路径点 Y_ref
phi_ref=zeros(Np,1); % Np 时域内的参考路径点 phi_ref
T_all=10;
for p=1:1:Np
if t+p*T>T_all % 临时设定,总的仿真时间,主要功能是防止计算期望轨迹越界
X_DOT=x_dot*cos(phi)-y_dot*sin(phi);%
X_predict(Np,1)=X+X_DOT*Np*T;
Y_ref(p,1)=polyval(Paramater_X_Y, X_predict(Np,1));
phi_ref(p,1)=polyval(Paramater_X_phi, X_predict(Np,1));
else
X_DOT=x_dot*cos(phi)-y_dot*sin(phi);
X_predict(p,1)=X+X_DOT*p*T;% 下一时刻 X(t)位置为 X+X_dot*t
Y_ref(p,1)=polyval(Paramater_X_Y, X_predict(p,1));
phi_ref(p,1)=polyval(Paramater_X_phi, X_predict(p,1));
end
end构建基于 Δu 的 kesi(k+1) 增广系统
%% 雅可比矩阵 a b
global a b;
global U;
delta_f=U(1);
a=[ 1 - (259200*T)/(1723*x_dot), -T*(phi_dot + (2*((460218*phi_dot)/5 - 62700*y_dot))/(1723*x_dot^2) - (133800*((154*phi_dot)/125 + y_dot))/(1723*x_dot^2)), 0, -T*(x_dot - 96228/(8615*x_dot)), 0, 0
T*(phi_dot - (133800*delta_f)/(1723*x_dot)), (133800*T*delta_f*((154*phi_dot)/125 + y_dot))/(1723*x_dot^2) + 1, 0, T*(y_dot - (824208*delta_f)/(8615*x_dot)), 0, 0
0, 0, 1, T, 0, 0
(33063689036759*T)/(7172595384320*x_dot), T*(((2321344006605451863*phi_dot)/8589934592000 - (6325188028897689*y_dot)/34359738368)/(4175*x_dot^2) + (5663914248162509*((154*phi_dot)/125 + y_dot))/(143451907686400*x_dot^2)), 0, 1 - (813165919007900927*T)/(7172595384320000*x_dot), 0, 0
T*cos(phi), T*sin(phi), T*(x_dot*cos(phi) - y_dot*sin(phi)), 0, 1, 0
-T*sin(phi), T*cos(phi), -T*(y_dot*cos(phi) + x_dot*sin(phi)), 0, 0, 1];
b=[ 133800*T/1723
T*((267600*delta_f)/1723 - (133800*((154*phi_dot)/125 + y_dot))/(1723*x_dot))
0
5663914248162509*T/143451907686400
0
0];
%% 构建基于Δu 的 kesi(k+1)增广状态
kesi=zeros(Nx+Nu,1);
kesi(1)=y_dot;
kesi(2)=x_dot;
kesi(3)=phi;
kesi(4)=phi_dot;
kesi(5)=Y;
kesi(6)=X;
kesi(7)=U(1);
%% kesi(k+1)系统的 A B C 增广系统
A_cell=cell(2,2);
B_cell=cell(2,1);
A_cell{1,1}=a;
A_cell{1,2}=b;
A_cell{2,1}=zeros(Nu,Nx);
A_cell{2,2}=eye(Nu);
B_cell{1,1}=b;
B_cell{2,1}=eye(Nu);
A=cell2mat(A_cell);
B=cell2mat(B_cell);
C=[0 0 1 0 0 0 0;0 0 0 0 1 0 0;];构建 PSI THETA GAMMA PHI 矩阵
%% 根据离散非线性模型预测下一时刻状态量 kesi(k+1,t),
state_k1=zeros(Nx,1);
state_k1(1,1)=y_dot+T*(-x_dot*phi_dot+2*(Ccf*(delta_f-(y_dot+lf*phi_dot)/x_dot)+Ccr*(lr*phi_dot-y_dot)/x_dot)/m);
state_k1(2,1)=x_dot+T*(y_dot*phi_dot+2*(Clf*Sf+Clr*Sr+Ccf*delta_f*(delta_f-(y_dot+phi_dot*lf)/x_dot))/m);
state_k1(3,1)=phi+T*phi_dot;
state_k1(4,1)=phi_dot+T*((2*lf*Ccf*(delta_f-(y_dot+lf*phi_dot)/x_dot)-2*lr*Ccr*(lr*phi_dot-y_dot)/x_dot)/I);
state_k1(5,1)=Y+T*(x_dot*sin(phi)+y_dot*cos(phi));
state_k1(6,1)=X+T*(x_dot*cos(phi)-y_dot*sin(phi));
%% dk 矩阵
d_k=zeros(Nx,1); % d(k,t) 构建
d_k=state_k1-a * kesi(1:6,1)-b * kesi(7,1); % d(k,t) 表达式
d_piao_k=zeros(Nx+Nu,1); % d(k,t) 增广形式d_piao_k
d_piao_k(1:6,1)=d_k;
d_piao_k(7,1)=0;
%% PSI THETA GAMMA PHI 矩阵
PSI_cell=cell(Np,1);
THETA_cell=cell(Np,Nc);
GAMMA_cell=cell(Np,Np);
PHI_cell=cell(Np,1)
for p=1:1:Np;
PHI_cell{p,1}=d_piao_k;%理论上来说,这个是要实时更新的,但是为了简便,这里又一次近似
for q=1:1:Np;
if q<=p;
GAMMA_cell{p,q}=C*A^(p-q);
else
GAMMA_cell{p,q}=zeros(Ny,Nx+Nu);
end
end
end
for j=1:1:Np
PSI_cell{j,1}=C*A^j;
for k=1:1:Nc
if k<=j
THETA_cell{j,k}=C*A^(j-k)*B;
else
THETA_cell{j,k}=zeros(Ny,Nu);
end
end
end
PSI=cell2mat(PSI_cell);
THETA=cell2mat(THETA_cell);
GAMMA=cell2mat(GAMMA_cell);
PHI=cell2mat(PHI_cell);Q R H E f 矩阵
%% Q R 矩阵
Q_cell=cell(Np,Np);
for i=1:1:Np;
for j=1:1:Np;
if i==j
Q_cell{i,j}=[2000 0;0 10000;];
else
Q_cell{i,j}=zeros(Ny,Ny);
end
end
end
Q=cell2mat(Q_cell);
R=1.1 * 10^5 * eye(Nu*Nc);
%% H 矩阵
H_cell=cell(2,2);
H_cell{1,1}=THETA'*Q*THETA+R;
H_cell{1,2}=zeros(Nu*Nc,1);
H_cell{2,1}=zeros(1,Nu*Nc);
Row=1000; % 松弛因子
H_cell{2,2}=Row;
H=cell2mat(H_cell);
H=(H+H')/2;
%% E 矩阵
E=zeros(Ny*Np,1);
Yita_ref_cell=cell(Np,1);
for p=1:1:Np
if t+p*T>T_all % 临时设定,总的仿真时间,主要功能是防止计算期望轨迹越界
Yita_ref_cell{p,1}=[phi_ref(p,1);Y_ref(p,1)];
else
Yita_ref_cell{p,1}=[phi_ref(p,1);Y_ref(p,1)];
end
end
Yita_ref=cell2mat(Yita_ref_cell);
E=Yita_ref - PSI * kesi - GAMMA * PHI;
%% f 矩阵
f_cell=cell(1,2);
f_cell{1,1}=2 * E' * Q * THETA;
f_cell{1,2}=0;
f=-cell2mat(f_cell);控制量约束、控制增量约束、输出约束
%% 约束条件
A_t=zeros(Nc,Nc); % 控制量约束
for p=1:1:Nc
for q=1:1:Nc
if q<=p
A_t(p,q)=1;
else
A_t(p,q)=0;
end
end
end
A_I=kron(A_t,eye(Nu));
Ut=kron(ones(Nc,1),U(1));
umin=-0.1744;
umax=0.1744;
delta_umin=-0.0148*0.4;
delta_umax=0.0148*0.4;
Umin=kron(ones(Nc,1),umin);
Umax=kron(ones(Nc,1),umax);
ycmax=[0.21;5];
ycmin=[-0.3;-3];
Ycmax=kron(ones(Np,1),ycmax);
Ycmin=kron(ones(Np,1),ycmin);
A_cons_cell={A_I zeros(Nu*Nc,1);-A_I zeros(Nu*Nc,1);THETA zeros(Ny*Np,1);-THETA zeros(Ny*Np,1)};
b_cons_cell={Umax-Ut;-Umin+Ut;Ycmax-PSI*kesi-GAMMA*PHI;-Ycmin+PSI*kesi+GAMMA*PHI};
A_cons=cell2mat(A_cons_cell);
b_cons=cell2mat(b_cons_cell);
M=10;
delta_Umin=kron(ones(Nc,1),delta_umin);
delta_Umax=kron(ones(Nc,1),delta_umax);
lb=[delta_Umin;0];%(求解方程)状态量下界,包含控制时域内控制增量和松弛因子
ub=[delta_Umax;M];%(求解方程)状态量上界,包含控制时域内控制增量和松弛因子quadprog() 求解、输出
%% quadprog()求解
% options = optimset('Algorithm','active-set');
options = optimset('Algorithm','interior-point-convex');
x_start=zeros(Nc+1,1);%加入一个起始点
[X,fval,exitflag]=quadprog(H,f,A_cons,b_cons,[],[],lb,ub,x_start,options);
%% 计算输出
u_piao=X(1); % 得到控制增量
U(1)=kesi(7,1)+u_piao; % 当前时刻的控制量 = 上一刻时刻控制 + 控制增量
sys= U;
toc4 Carsim / Simulink联合仿真
4.1 Carsim 设计
新建 Dataset
选择车型
修改车身参数
新建仿真工况 Dataset
设置仿真工况
关联到 Simulink
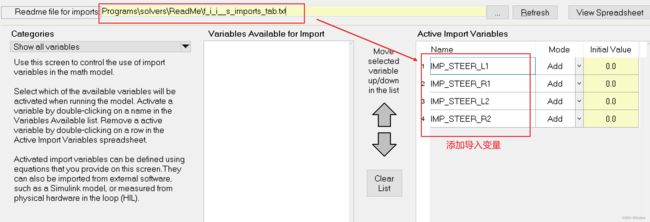
添加导入变量
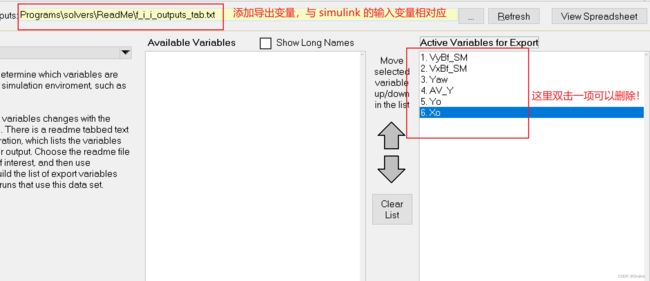
添加导出变量
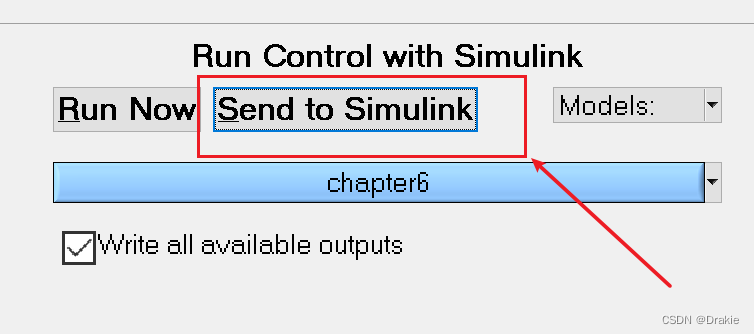
将 Carsim 模型输出到 Simulink
开启 Simulink 模块
4.3 不同车速跟踪验证
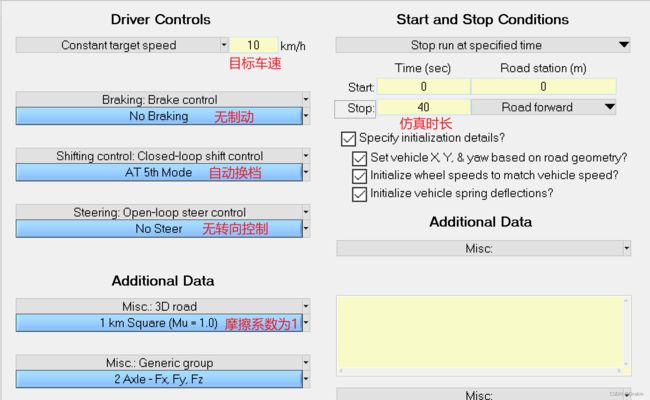
设计仿真工况,测试轨迹跟随控制系统在不同速度下的跟踪能力。依然以双移线轨迹作为车辆的全局参考轨迹,设定工况如下。
轨迹跟踪仿真实验分别在低速、中速、高速几个情况下进行,道路附着条件良好,u = 1。参考轨迹上存在一个障碍物,膨胀后的尺寸为 5 m × 2 m,角点的坐标位置为(30,0.5),也就是第一个 obstacle 的位置。
上层轨迹规划 MPC 所采用的参数为:T=0.1s,Np=15,Nc=2,Q=10,R=5,Sobs=10;
下层跟踪控制 MPC 所采用的参数为:T=0.05s,Np=25,Nc=10,Q=10,R=5,ρ=1000;
中低速:36 Km/h,跟踪效果良好
低速:20 Km/h,可以跟踪,效果较差
超低速:10 Km/s,跟踪失败
超低速跟踪失败原因分析:
对比低速和整车速度的小车轨迹,可以发现低速情况下小车轨迹在障碍物上方,而正常10m/s 情况下,车辆从障碍物下方穿过。这是因为根据车速的不同,在可视时域 Np 即预测时域内,小车寻找到的最远轨迹点不同从而做出不同的选择。
车速越快,则看得越远,即高速前进的小车在起点位置不远处就可以观察到障碍物的位置,从而结合全局参考路径,更合理地选择从障碍物下方穿越,这样既保证了与障碍物的安全距离,更在很大程度上保证了未来Np时域内与参考路径的误差范数最小。
而低速情况下,小车在有限的 Np 时域内观察到的参考轨迹也有限,如果障碍物本身的尺寸比预测时域内小车前进的距离都大,则小车甚至无法同时顾及位置跟踪及障碍物安全距离,由于与避障惩罚系数远大于轨迹跟踪误差系数,小车会优先选择避开障碍物,导致在一定时间内与参考路径渐行渐远,甚至出现无法跟随的现象。
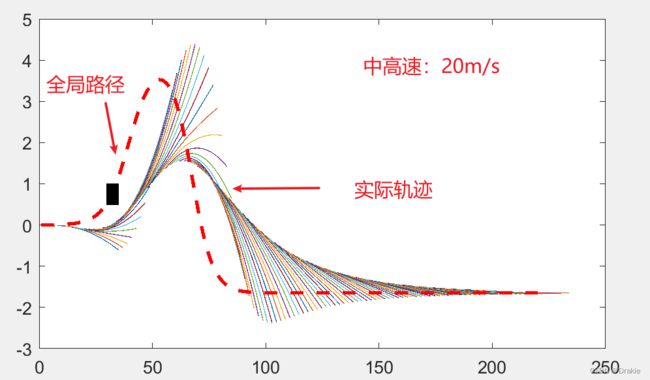
中高速:72 Km/h,跟踪良好
车速为 20m/s,即 72 km/h,可以看到跟踪效果良好
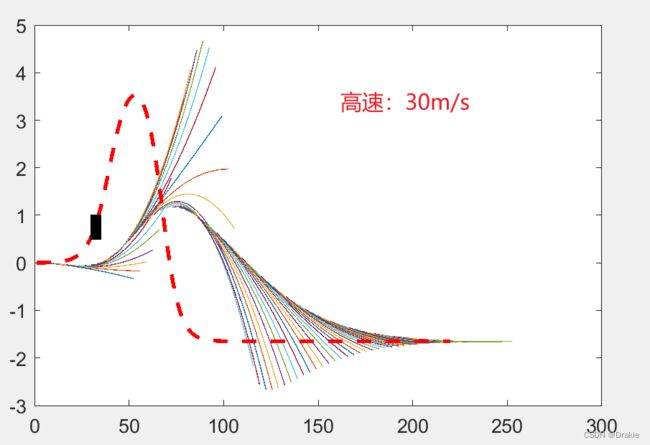
高速:108 Km/h,跟踪良好(不考虑侧倾稳定性)
验证车速为 30m/s,即 108 Km/h 的高速跟踪效果,可以看见局部路径随着速度的提高而变长,从而更合理地规划出局部路径,过高的速度需要考虑轮胎滑移率、侧倾稳定性等,本节没有涉及。
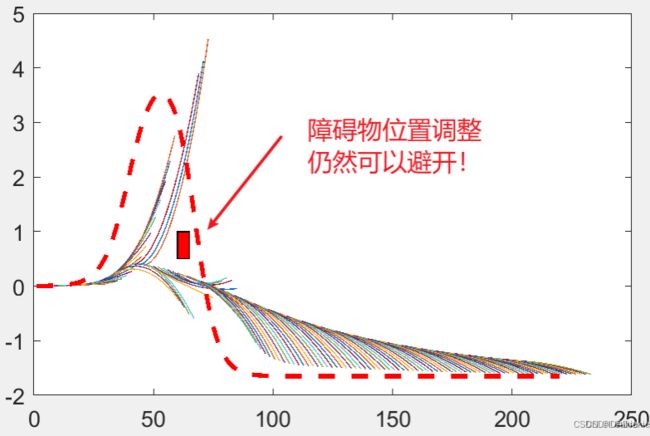
调整障碍物位置,观察避障效果
避障效果:
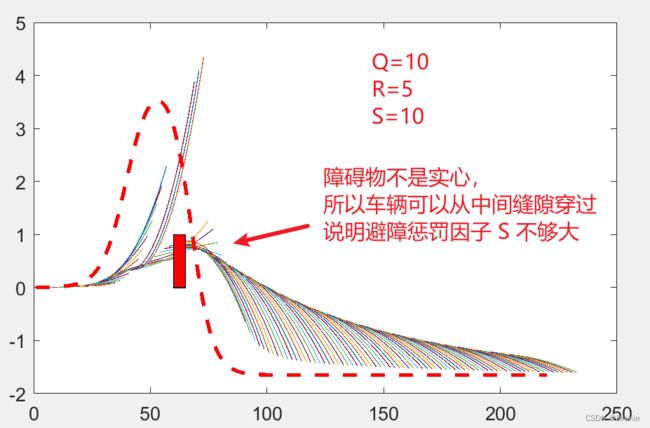
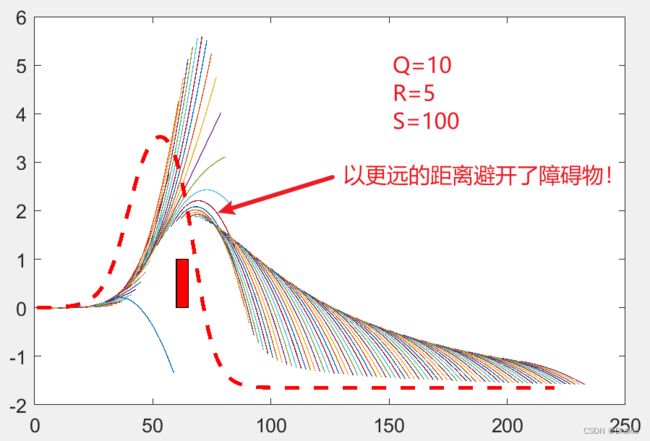
避障系数 S 的影响
调大 S 系数: