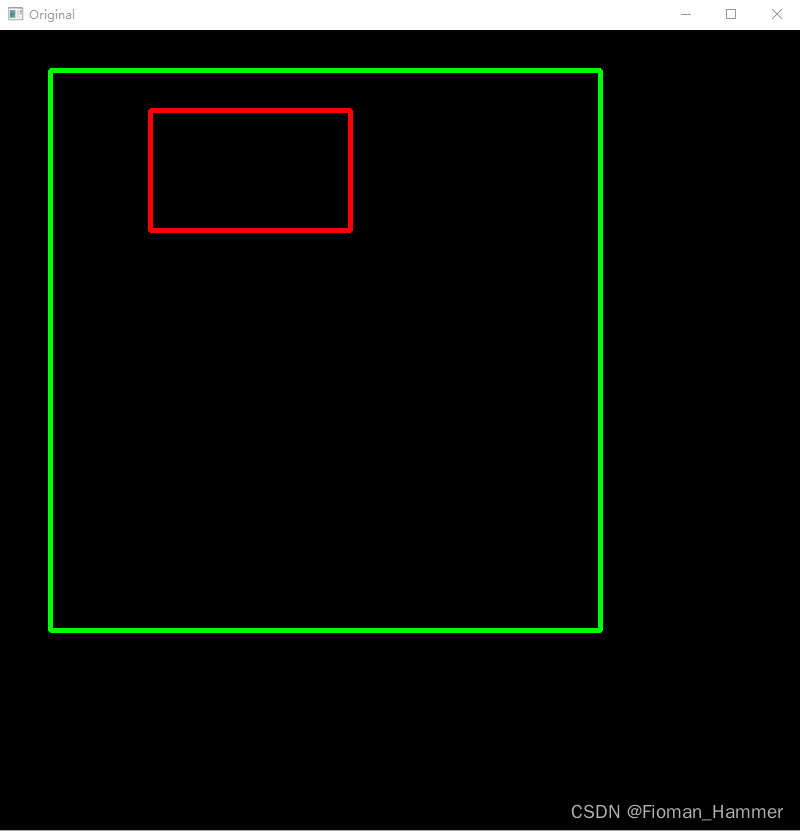
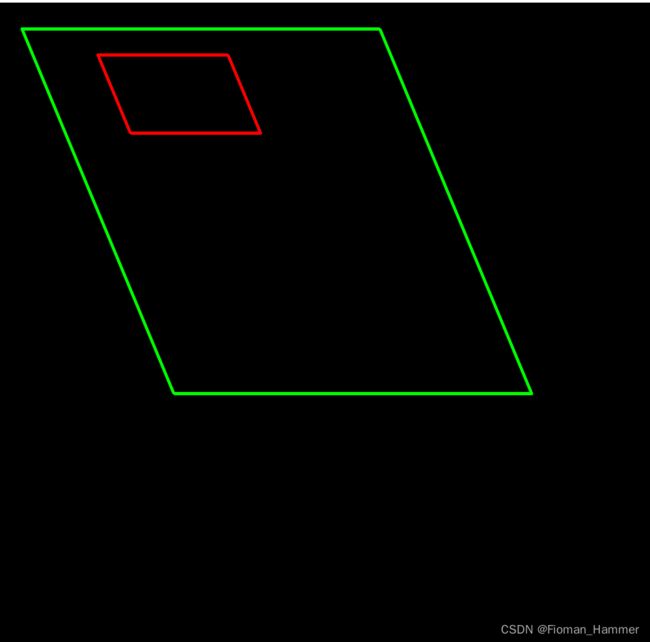
Opencv_10 图像的透视变换

一. 透视变换的原理

透视变换(Perspective Transformation)是将图片投影到一个新的视平面(Viewing Plance),也称为投影映射(Projective Mapping).通用的变换公式为:

透视变换矩阵

(x,y,1)是原点, [X,Y,Z]是变换后的点位

这是一个二维空间变换到三维空间的转换,因为图像在二维平面,故除以Z

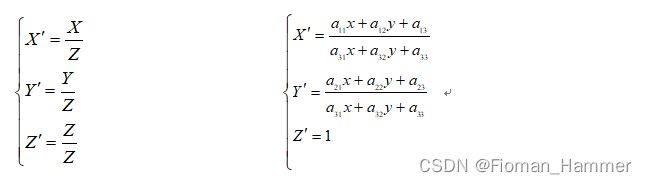
二. 透视变换实现

① 函数原型

Mat getPerspectiveTransform(const Point2f src[], const Point2f dst[], 
							int solveMethod = DECOMP_LU);

参数说明:

• src[]: 原图像中的四个像素坐标
• dst[]: 目标图像中的四个像素点坐标
• solveMethod: 选择计算透视变换矩阵方法的标志,可以选择参数以及含义在下表中

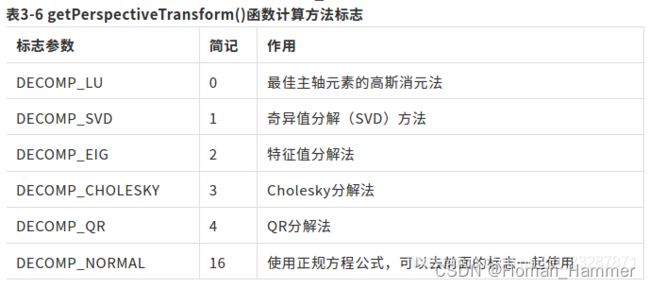
该函数两个输入量都是存放浮点坐标的数组,在生成数组的时候像素点的输入顺序没有要求,但是需要注意像素点的对应关系是一一对应的,函数的返回值是一个3*3的矩阵.最后一个参数是对应点坐标计算透视变换矩阵方法的选择标志,默认使用的是最佳主轴元素的高斯消元法DECOMP_LU

获取到透视变换矩阵以后,就可以进行透视变换了

void warpPerspective( InputArray src, OutputArray dst,
                                   InputArray M, Size dsize,
                                   int flags = INTER_LINEAR,
                                   int borderMode = BORDER_CONSTANT,
                                   const Scalar& borderValue = Scalar());

参数说明:

• src: 输入图像
• dst: 输出图像
• M: 3*3的变换矩阵
• dSize: 输出图像的尺寸
• flags: 插值方法标志
• boardMode: 像素边界填充方式的标志
• boardValue: 填充边界使用的数值,默认情况下是0

② 透视变换实现

#include"MyOpencv.h"
#include 

int main(void)
{
	Mat imageSrc = Mat::zeros(Size(800, 800), CV_8UC3);
	// 画一个多边形
	vector<Point> pts;
	pts.push_back(Point(50, 40));
	pts.push_back(Point(600, 40));
	pts.push_back(Point(600, 600));
	pts.push_back(Point(50, 600));

	polylines(imageSrc, pts, true, Scalar(0, 255, 0), 3, LINE_8);

	pts.clear();
	pts.push_back(Point(150, 80));
	pts.push_back(Point(350, 80));
	pts.push_back(Point(350, 200));
	pts.push_back(Point(150, 200));
	polylines(imageSrc, pts, true, Scalar(0, 0, 255), 3, LINE_8);

	Point2f srcPoint[4];
	Point2f dstPoint[4];

	srcPoint[0] = Point2f(150, 80);
	srcPoint[1] = Point2f(350, 80);
	srcPoint[2] = Point2f(350, 200);
	srcPoint[3] = Point2f(150, 200);

	dstPoint[0] = Point2f(150, 80);
	dstPoint[1] = Point2f(350, 80);
	dstPoint[2] = Point2f(400, 200);
	dstPoint[3] = Point2f(200, 200);

	Mat M = getPerspectiveTransform(srcPoint, dstPoint);
	Mat dst;
	warpPerspective(imageSrc, dst, M, Size(1000, 1000));
	imshow("Original", imageSrc);
	imshow("Dst", dst);
	waitKey(0);

	return 0;
} 

结果:

三. 透视变换的案例

将这张图像摆正.用到的技术.

1. 灰度处理,二值化,形态学操作行程连通域
2. 轮廓发现,将目标的轮廓绘制出来
3. 在绘制的轮廓中进行直线检测
4. 找出4个边,求出四个交点
5. 使用透视变换函数,得到结果

#include "MyOpencv.h"
#include 

int main(void)
{
	Mat imageSrc = imread("./test_01.png", IMREAD_GRAYSCALE);
	imshow("Original", imageSrc);
	// 二值化
	Mat binary;
	threshold(imageSrc, binary, 0, 255, THRESH_BINARY | THRESH_OTSU);
	imshow("Binary", binary);

	// 形态学 开操作,可以填充白色小区域
	Mat morphImage;
	Mat kernel = getStructuringElement(MORPH_RECT, Size(5, 5), Point(-1, -1));
	morphologyEx(binary, morphImage, MORPH_OPEN, kernel, Point(-1, -1), 3);
	imshow("Opened", morphImage);

	// 查找轮廓
	vector<vector<Point>> contours;
	vector<Vec4i> hireachy;
	findContours(morphImage, contours, hireachy, RETR_LIST, CHAIN_APPROX_SIMPLE);
	cout << "Contours.size: " << contours.size() << endl;

	// 轮廓绘制
	int width = imageSrc.cols;
	int height = imageSrc.rows;
	Mat drawImage = Mat::zeros(imageSrc.size(), CV_8UC3);

	for (int index = 0; index < contours.size(); index++)
	{
		Rect rect = boundingRect(contours[index]);
		if (rect.width > width / 2 && rect.height > height / 2 
		&& rect.width < width - 5 && rect.height < height - 5)
		{
			drawContours(drawImage, contours, index, Scalar(0, 0, 255), 2, 8,
						 hireachy, 0, Point(0, 0));
		}
	}
	imshow("Contours", drawImage);

	// 直线检测
	vector<Vec4i> lines;
	Mat contoursImage;
	int accu = static_cast<int>(min(width * 0.3, height * 0.3));
	cvtColor(drawImage, contoursImage, COLOR_BGR2GRAY);
	imshow("Contours", contoursImage);

	Mat linesImage = Mat::zeros(imageSrc.size(), CV_8UC3);
	HoughLinesP(contoursImage, lines, 1, CV_PI / 180.0,150,accu,accu);

	for (int index = 0; index < lines.size(); index++)
	{
		Vec4i ln = lines[index];
		line(linesImage, Point(ln[0], ln[1]), Point(ln[2], ln[3]),
		 Scalar(0, 0, 255), 2, 8, 0);
	}

	cout << "Number of lines: " << lines.size() << endl;
	imshow("ImageLines",linesImage);

	// 先确定上下左右四条直线,然后求交点
	Vec4i topLine, bottomLine, leftLine, rightLine;
	int yOffset;
	int xOffset;
	for (int i = 0; i < lines.size(); i++)
	{
		Vec4i line = lines[i];
		yOffset = abs(line[3] - line[1]);
		xOffset = abs(line[0] - line[2]);

		// topLine and bottomLine
		if (yOffset < height * 0.2 )
		{
			if (line[1] < height / 2 && line[3] < height / 2)
			{
				topLine = lines[i];
			}
			else
			{
				bottomLine = lines[i];
			}
		}

		// leftLine and rightLine
		if (xOffset < width * 0.2)
		{
			if (line[0] < width / 2 && line[1] < width / 2)
			{
				leftLine = lines[i];
			}
			else
			{
				rightLine = lines[i];
			}
		}

	}

	cout << "topLine : p1(x,y)= " << topLine[0] << "," << topLine[1] << 
	"; p2(x,y)= " << topLine[2] << "," << topLine[3] << endl;
	cout << "bottomLine : p1(x,y)= " << bottomLine[0] << "," << bottomLine[1] << 
	"; p2(x,y)= " << bottomLine[2] << "," << bottomLine[3] << endl;
	cout << "leftLine : p1(x,y)= " << leftLine[0] << "," << leftLine[1] << 
	"; p2(x,y)= " << leftLine[2] << "," << leftLine[3] << endl;
	cout << "rightLine : p1(x,y)= " << rightLine[0] << "," << rightLine[1] << 
	"; p2(x,y)= " << rightLine[2] << "," << rightLine[3] << endl;


	// 获取两条直线的交点
	Point leftTop, rightTop, rightBottom, leftBottom;

	float leftLineK, leftLineB, topLineK, topLineB, 
	      rightLineK, rightLineB, bottomLineK, bottomLineB;
	leftLineK = float(leftLine[3] - leftLine[1]) / float(leftLine[2] - leftLine[0]);
	leftLineB = leftLine[1] - leftLineK * leftLine[0];

	rightLineK = float(rightLine[3] - rightLine[1]) / float(rightLine[2] - rightLine[0]);
	rightLineB = rightLine[1] - rightLineK * rightLine[0];

	topLineK = float(topLine[3] - topLine[1]) / float(topLine[2] - topLine[0]);
	topLineB = topLine[1] - topLineK * topLine[0];

	bottomLineK = float(bottomLine[3] - bottomLine[1]) /
				  float(bottomLine[2] - bottomLine[0]);
	bottomLineB = bottomLine[1] - bottomLineK * bottomLine[0];
	cout << "leftLineK = " << leftLineK << ", leftLineB = " << leftLineB << endl;
	cout << "rightLineK = " << rightLineK << ", rightLineB = " << rightLineB << endl;
	cout << "topLineK = " << topLineK << ", topLineB = " << topLineB << endl;
	cout << "bottomLineK = " << bottomLineK << ", bottomLineB = " << bottomLineB << endl;


	// 获取交点
	Point p1;
	p1.x = -static_cast<int>((leftLineB - topLineB) / (leftLineK - topLineK));
	p1.y = static_cast<int>(leftLineK * p1.x + leftLineB);

	Point p2;
	p2.x = -static_cast<int>((topLineB - rightLineB) / (topLineK - rightLineK));
	p2.y = static_cast<int>(topLineK * p2.x + topLineB);

	Point p3;
	p3.x = -static_cast<int>((rightLineB - bottomLineB) / (rightLineK - bottomLineK));
	p3.y = static_cast<int>(rightLineK * p3.x + rightLineB);

	Point p4;
	p4.x = -static_cast<int>((bottomLineB - leftLineB) / (bottomLineK - leftLineK));
	p4.y = static_cast<int>(bottomLineK * p4.x + bottomLineB);

	cout << "Point p1: (" << p1.x << "," << p1.y << ")" << endl;
	cout << "Point p2: (" << p2.x << "," << p2.y << ")" << endl;
	cout << "Point p3: (" << p3.x << "," << p3.y << ")" << endl;
	cout << "Point p4: (" << p4.x << "," << p4.y << ")" << endl;

	// 获取两点之间的距离'
	int newWidth, newHeight;

	newWidth = sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y) * (p1.y - p2.y));
	newHeight = sqrt((p1.x - p4.x) * (p1.x - p4.x) + (p1.y - p4.y) * (p1.y - p4.y));

	cout << "newWidth = " << newWidth << ", newHeight = " << newHeight << endl;

	// 透视变换
	Point2f srcPts[4];
	Point2f dstPts[4];
	
	srcPts[0] = p1;
	srcPts[1] = p2;
	srcPts[2] = p3;
	srcPts[3] = p4;

	dstPts[0] = Point(0, 0);
	dstPts[1] = Point(newWidth, 0);
	dstPts[2] = Point(newWidth, newHeight);
	dstPts[3] = Point(0, newHeight);

	Mat M = getPerspectiveTransform(srcPts, dstPts, 0);
	Mat dst;
	warpPerspective(imageSrc, dst, M, Size(newWidth+5, newHeight+5), INTER_LINEAR);
	imshow("Dst", dst);

	waitKey(0);
	return 0;
} 

结果: