分类问题的评价指标(Precision、Recall、Accuracy、F1-Score、Micro-F1、Macro-F1)以及混淆矩阵、ROC曲线
文章目录
- 一、四个基本概念 TP、FP、TN、FN
- 二、精确率(precision)、召回率(recall)、准确率(accuracy)
- 三、F1-Score(F1分数)
- 四、宏平均 Macro-F1 、微平均 Micro-F1、加权平均 Weighted avg
- 五、混淆矩阵(Confusion Matrix)
- 六、ROC 曲线和 AUC(Area Under the Curve,曲线下面积)
一、四个基本概念 TP、FP、TN、FN
真阳性:预测为正,实际为正。把正样本成功预测为正。 TP——True Positive
假阳性:预测为正,实际为负。把负样本错误预测为正。 FP——False Positive ——>误报
真阴性:预测为负、实际为负。把负样本成功预测为负。 TN——True Negative
假阴性:预测与负、实际为正。把正样本错误预测为负。 FN——False Negative ——>漏报
注:一致判真假,预测判阴阳

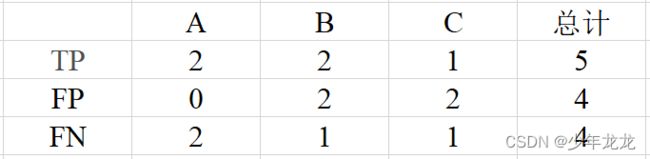
1、真阳性:指预测正确,是哪个类就被分到哪个类。对A而言,TP个数为 2;对B而言,TP个数为 2;对C而言,TP个数为 1。
2、假阳性:就是指预测为某个类,但是实际上不是。对A而言,FP个数为 0;对B而言,FP个数为 2;对C而言,FP个数为 2。(因为"3"和"8"都不是B类,但却分给了B,所以为假阳性)
3、假阴性:对A而言,FN个数为 2;对B而言,FN个数为 1;对C而言,FN个数为 1。(因为"3"和"4"分别预测为B和C,但是实际是A,也就是预测为负,实际为正)
二、精确率(precision)、召回率(recall)、准确率(accuracy)
1、精确率(查准率):计算预测出来的某类样本中,有多少是被正确预测的。即表示的是预测为正的样本中有多少是真正的正样本。针对预测样本而言。
2、召回率(查全率):有多少样本被正确的预测出来了,即该类样本有多少被找出来(召回了多少)。即表示的是样本中的正例有多少被预测正确了。针对原先实际样本而言。
3、准确率:正类和负类预测准确的比例。在正例较少负例较多的不平衡分类问题(疾病;恐怖分子)中,存在着如果把所有数据全部预测为负例,准确率依然会很高的问题,所以引入召回率。
根据多分类结果,可以根据样本的预测结果是否正确来形成混淆矩阵。

(1)加权准确率(Weighted Accuracy,WA)

(2)非加权准确率(Unweighted Accuracy,UA)

精确率:
precision= TP / (TP + FP)
召回率:recall= TP / (TP + FN)
准确率:accuracy= (TP + TN) / (TP+ FP + TN + FN)
F1 Score = 2P*R/(P+R),其中P和R分别为 precision 和recall
注:精确率和召回率分别对应着从主客观两个不同的维度来看TP,也就是对正例的预测效果。它们其实就是分母不同,一个分母是预测为正的样本数,另一个是原来样本中所有的正样本数。
(1)Precision的分母是 (TP+FP),表示的是所有预测为正的例子数。所以Precision代表的是在所有预测为正的例子中,实际上真的为正的比例。预测这个动作代表的是主观,所以Precision表示的是主观上针对正例的预测效果好不好。
(2)Recall的分母是 (TP+FN),表示的是所有实际为正的例子数。所以Recall代表的是在所有实际为正的例子中,预测对了的比例。实际上有多少正例是一个客观存在的事实,所以Recall表示的是客观上针对正例的预测效果好不好。
4、举例计算
(1)某池塘有1400条鲤鱼,300只虾,300只鳖。现在以捕鲤鱼为目的。撒一大网,逮着了700条鲤鱼,200只虾,100只鳖。
解:可以把上述例子看成分类预测问题,对于鲤鱼来说,TP真阳性为700,FP假阳性为300,FN假阴性为700。
Precison = TP/(TP+FP) = 700(700+300) = 70%
Recall = TP/(TP+FN) = 700/(700+700) = 50%
(2)改变上述例子:把池子里所有的鲤鱼、虾和鳖都一网打尽,再观察这些指标的变化。
解:TP为1400,有1400条鲤鱼被预测出来;FP为600,有600个生物不是鲤鱼类,却被归类到鲤鱼;FN为0,鲤鱼都被归类到鲤鱼类去了,并没有归到其他类。
Precision = TP/(TP+FP) = 1400/(1400+600) = 70%
Recall = TP/(TP+FN) = 1400/(1400) = 100%
总结:预测时当然希望Precision和Recall都保持一个较高的水准,但事实上这两者在某些情况下是有矛盾的。比如在极端情况下,倘若只搜索出了一个结果,且是正确的,那么Precision就是100%,但是Recall就很低;而如果把所有结果都返回,那么比如Recall是100%,但是Precision就会很低。因此在不同的场合中需要自己判断希望Precision比较高或是Recall比较高,此时可以引出另一个评价指标 F1-Score(F-Measure)。
三、F1-Score(F1分数)
F1分数(F1 Score)是统计学中用来衡量二分类模型精确度的一种指标,它同时兼顾了分类模型的精确率和召回率。F1分数可以看作是模型精确率和召回率的一种加权平均,它的最大值是1,最小值是0。
数学定义:F1-Score又称为平衡F分数(BalancedScore),它被定义为精确率和召回率的调和平均数。
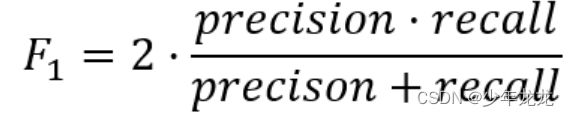
更一般的,定义Fβ分数为:

除了F1分数之外,F0.5分数和F2分数,在统计学中也得到了大量应用,其中,F2分数中,召回率的权重高于精确率,而F0.5分数中,精确率的权重高于召回率。
注:推导F-score理解其精髓

从上式子可以看出F-score只和 FP/TP 、FN/TP 两个东西有关。结合前面所述:
FP/TP影响的是主观判断上TP够不够分量,也就是主观上TP这个值到底够不够大;
FN/TP影响的是客观判断上TP够不够分量,也就是客观上TP这个值到底够不够大;
故而做极限假设,看一下F-score什么时候等于0,什么时候等于1:
(1)F-score = 0 (实际上是无限趋近于0)
主观上TP很小 or 客观上TP很小
即 FP 或 FN 远大于TP,这里做极限假设可以知道F-score趋近于0
(2)F-score = 1
主观上和客观上来说TP都很大,也就是FP和FN都等于0(下限)。
总结:直觉上来说TP越大越好,但是这里的大肯定是一个相对的概念,而F-score 就是分别从两个角度,主观(Predicted)和客观(Actual)上去综合的分析TP够不够大。这也就是平常看到的结论 F-score的值 只有在 Precision 和 Recall 都大的时候 才会大。
四、宏平均 Macro-F1 、微平均 Micro-F1、加权平均 Weighted avg
在一个多标签分类任务中,可以对每个“类”计算F1,显然需要把所有类的F1合并起来考虑。这里有两种合并方式:
(1)第一种计算出所有类别总的Precision和Recall,然后计算F1。
例如依照最上面的表格来计算:Precison=5/(5+4)=0.556,Recall=5/(5+4)=0.556,然后带入F1的公式求出F1,这种方式被称为Micro-F1微平均。
(2)第二种方式是计算出每一个类的Precison和Recall后计算F1,最后将F1平均。
例如上式A类:P=2/(2+0)=1.0,R=2/(2+2)=0.5,F1=(210.5)/1+0.5=0.667。同理求出B类C类的F1,最后求平均值,这种方式叫做Macro-F1宏平均。
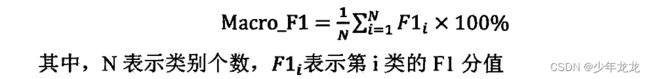
注:微平均 Micro-F1 主要应用在样本数据分布均衡的数据集上,而宏平均Macro-F1 主要应用在样本数据分布不均衡的数据集上,因为它在分类结果中更能照顾小规模样本的权重。
举例计算:
使用 sklearn.metric.classification_report 工具对模型的测试结果进行评价时,会有如下输出结果(support是数据量):
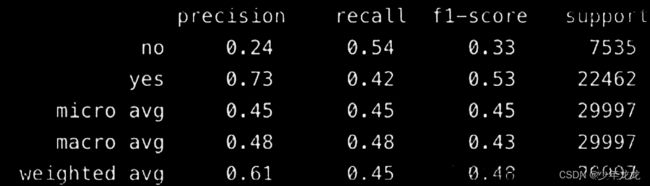
(1)宏平均 macro avg:对每个类别的 精准、召回和F1 加和求平均。
macro avg = (P_no+P_yes)/2=(0.24+0.73)/2 = 0.48
(2)微平均 micro avg:不区分样本类别,计算整体的 精准、召回和F1
micro avg = (P_nosupport_no+P_yessupport_yes)/(support_no+support_yes)=(0.247535+0.73)/(7535+22462)=0.45
(3)加权平均 weighted avg:是对宏平均的一种改进,考虑了每个类别样本数量在总样本中占比。
weighted avg =P_no*(support_no/support_all)+ P_yes*(support_yes/support_all =0.24*(7525/29997)+0.73*(22462/29997)=0.61
五、混淆矩阵(Confusion Matrix)
在机器学习领域,混淆矩阵又称为可能性表格或错误矩阵。它是一种特定的矩阵,用来呈现算法性能的可视化效果,通常是监督学习(非监督学习通常用匹配矩阵:matching matrix)。其每一列代表预测值,每一行代表的是实际的类别。这个名字来源于它可以非常容易的表明多个类别是否有混淆(也就是一个class被预测成另一个class)。一个二分类(正和反)问题的混淆矩阵如下图所示:


在n分类模型中,使用n行n列的矩阵形式来表示精度,纵列代表n个分类,在每行中的n个数据代表分别预测在每个类别的个数,完美的预测应该是一个列序数=行中有数据的索引数的一条斜线。

实例:
假设有一个用来对猫(cats)、狗(dogs)、兔子(rabbits)进行分类的系统,混淆矩阵就是为了进一步分析性能而对该算法测试结果做出的总结。假设总共有 27 只动物:8只猫, 6条狗, 13只兔子。结果的混淆矩阵如下图所示:

在这个混淆矩阵中,实际有 8只猫,但是系统将其中3只预测成了狗;对于 6条狗,其中有 1条被预测成了兔子,2条被预测成了猫。从混淆矩阵中我们可以看出系统对于区分猫和狗存在一些问题,但是区分兔子和其他动物的效果还是不错的。所有正确的预测结果都在主对角线上,所以从混淆矩阵中可以很方便直观的看出哪里有错误,因为他们呈现在对角线外面。
注:在预测分析中,混淆表格(有时候也称为混淆矩阵),是由false positives,falsenegatives,true positives和true negatives组成的两行两列的表格。它允许我们做出更多的分析,而不仅仅是局限在正确率。准确率对于分类器的性能分析来说,并不是一个很好地衡量指标,因为如果数据集不平衡(每一类的数据样本数量相差太大),很可能会出现误导性的结果。例如,如果在一个数据集中有95只猫,但是只有5条狗,那么某些分类器很可能偏向于将所有的样本预测成猫。整体准确率为95%,但是实际上该分类器对猫的识别率是100%,而对狗的识别率是0%。
六、ROC 曲线和 AUC(Area Under the Curve,曲线下面积)
ROC曲线展示了当改变在模型中识别为正例的阈值时,召回率和精度的关系会如何变化。计算公式如下:
![]()
TPR = TP / (TP + FN) TPR 是召回率
FPR = FP / (FP + TN) FPR 是反例被报告为正例的概率
一个典型的 ROC 曲线如下:

黑色对角线表示随机分类器,红色和蓝色曲线表示两种不同的分类模型。对于给定的模型,只能对应一条曲线,但是可以通过调整对正例进行分类的阈值来沿着曲线移动。通常,当降低阈值时,会沿着曲线向右和向上移动。
在阈值为 1.0 的情况下,将位于图的左下方,因为没有将任何数据点识别为正例,这导致没有真正例,也没有假正例(TPR = FPR = 0)。当降低阈值时,将更多的数据点识别为正例,导致更多的真正例,但也有更多的假正例 ( TPR 和 FPR 增加)。最终,在阈值 0.0 处,将所有数据点识别为正,并发现位于 ROC 曲线的右上角 ( TPR = FPR = 1.0 )。
最后,可以通过计算曲线下面积 ( AUC ) 来量化模型的 ROC 曲线,这是一个介于 0 和 1 之间的度量,数值越大,表示分类性能越好。在上图中,蓝色曲线的 AUC 将大于红色曲线的 AUC,这意味着蓝色模型在实现准确度和召回率的权衡方面更好。随机分类器 (黑线) 实现 0.5 的 AUC。
参考资料:
https://zhuanlan.zhihu.com/p/161703182
https://blog.csdn.net/vesper305/article/details/44927047
https://blog.csdn.net/sinat_28576553/article/details/80258619
https://blog.csdn.net/duan19920101/article/details/121726392
https://blog.csdn.net/weixin_43090631/article/details/107208216