FedNCF:Federated Neural Collaborative Filtering | 联邦神经协同过滤
论文信息
- 标题:FedNCF: Federated Neural Collaborative Filtering
- 作者:Vasileios Perifanis ∗ ^* ∗, Pavlos S. Efraimidis
- 发表年份:2022
- doi:10.1016/j.knosys.2022.108441
Abstract
\qquad 在这项工作中,我们提出了最先进的神经协同过滤(NCF)方法的联邦版本,用于物品推荐。该算法名为FedNCF,无需用户暴露或传输原始数据就能进行训练。数据本地化既保护了数据隐私,又符合GDPR等法规。尽管联邦学习可以在不传播本地数据的情况下进行模型训练,但原始客户端更新的传输会引发额外的隐私问题。为了应对这一挑战,我们引入了一种保护隐私的聚合方法,它可以满足用户的安全需求。我们从理论上和实验上论证了现有的聚合算法与潜在因子模型的更新不一致。我们提出了一种改进方法,将聚合步骤分解为矩阵分解和基于神经网络的平均。实验验证表明,FedNCF的推荐质量与原始NCF系统相当,而与现有方法相比,我们提出的聚合能够更快的收敛。我们研究了联邦推荐系统的有效性,并从计算成本的角度评估了隐私保护机制。
Introduction
- 推荐系统广泛应用与个性化预测模型,帮助用户识别感兴趣的物品。系统常会收集各种显式反馈(个人背景、评分等)和隐式反馈(与物品的交互)。提供一个基于过去的交互预测未来的偏好,常常被用于电子商务和在线流媒体服务。最常见的推荐系统采用协同过滤(CF)。
- 在集中式学习的情况下,被GDPR等隐私法规和法律的限制,自从联邦学习的出现促进了在不搜集用户信息的机器学习发展,并且在隐私和快速分布式计算方面都有很大的进步。
- 联邦推荐研究仍有不足,并且联邦算法仍然有泄露隐私的分险。服务器可以通过用户上传的参数与全局模型之间的差异推断用户交互的物品有哪些,因为用户只更新交互物品的嵌入。
- 由于服务器能够从用户上传的物品嵌入推断用户交互的物品,所以本文使用SecAvg进行加密。
Federated neural collaborative filtering
Problem definition
- 本地数据不上传
- 用户的数据是non-iid
Notations and Desription
FedNCF中参数的注释和说明
| Notation | Description |
|---|---|
| M M M | 用户数量 |
| N N N | 物品数量 |
| D D D | 潜在因子维数 |
| u ∈ { 1 , 2 , . . . , M } u \in \{1,2,...,M \} u∈{1,2,...,M} | 用户的id |
| i ∈ { 1 , 2 , . . . , N } i \in \{ 1,2,...,N\} i∈{1,2,...,N} | 物品的id |
| r r j ∈ { 0 , 1 } r_{rj} \in \{0,1 \} rrj∈{0,1} | 用户 i i i和物品 j j j的交互 |
| I I I | 共享物品潜在因子向量 |
| U i U_i Ui | 用户潜在因子向量 |
| N N N | 神经网络权重 |
| P i = { U i , I , R i } \mathcal{P}_i = \{U_i, I, R_i \} Pi={Ui,I,Ri} | 用户偏好集合 |
| C ⊆ P C \subseteq \mathcal{P} C⊆P | 可以获得客户端数量 |
| c ⊆ C c \subseteq C c⊆C | 随机选择的客户端 |
| M I MI MI | 加密物品嵌入权重 |
| M N MN MN | 加密的神经网络权重 |
| M P MP MP | 加密的用户的交互的隐式反馈向量 |
| E E E | 本地更新轮数 |
Definition
- 用户更新后的物品嵌入、神经网络权重、用户交互的物品隐式反馈使用SMC加密上传。
- 交互 r r r进行二值化,使用隐式反馈。
- 用户嵌入向量不上传。
FedNCF架构
FedNCF架构一共有三种算法:FedGMF、FedMLP、FedNeuMF。

-
首先服务器初始化权重 W t = { I t , N t } W_t =\{I_t,N_t \} Wt={It,Nt}
-
然后随机选择 c ⊆ C ⊆ P c \subseteq C \subseteq \mathcal{P} c⊆C⊆P个用户
-
将权重 W t W_t Wt广播到用户 c c c
-
c中每个用户进行epoch轮更新得到参数 U t + 1 , I t + 1 , N t + 1 U_{t+1},I_{t+1},N_{t+1} Ut+1,It+1,Nt+1
-
本地用户更新用户嵌入
-
本地用户上传 I t + 1 , N t + 1 I_{t+1},N_{t+1} It+1,Nt+1
-
服务器聚合参 I t + 1 , N t + 1 = ∑ t − 1 ∣ c ∣ N t + 1 I_{t+1}, N_{t+1}=\begin{matrix} \sum_{t-1}^{|c|} N_{t+1}\end{matrix} It+1,Nt+1=∑t−1∣c∣Nt+1

与前面不同的是在本地用户跟新后的步骤,之前的步骤一样。 -
首先每个用户与其他用户交换随机种子,大家共用一个随机种子矩阵。
-
使用随机种子 s e e d i j seed_{ij} seedij生成随机矩阵 I R i j , IR_{ij}, IRij, N R i j NR{ij} NRij和随机向量 P R i j PR_{ij} PRij,这里每种矩阵或向量都有 ∣ c ∣ − 1 |c|-1 ∣c∣−1个。
-
上传 M I t + 1 , M N t + 1 , M P t + 1 MI_{t+1}, MN_{t+1}, MP_{t+1} MIt+1,MNt+1,MPt+1
-
服务器计算每个物品嵌入被更新的次数 n u m k = ∑ i = 1 ∣ c ∣ M P i k num_k=\begin{matrix}\sum_{i=1}^{|c|}MP_i^k \end{matrix} numk=∑i=1∣c∣MPik, M P i k MP_i^k MPik是一个 c c c维向量,它的每一个值表示表示一个用户的隐式反馈,即0和1,所以加起来为物品 i i i被 m u n k mun_k munk个用户更新,并对 M N i k MN_i^k MNik聚合 ∑ i = 1 ∣ c ∣ M I i k / n u m k \begin{matrix}\sum_{i=1}^{|c|}MI_i^k/num_k \end{matrix} ∑i=1∣c∣MIik/numk。 c c c个用户的数据集数量 n = ∑ i = 1 D n u m k n=\begin{matrix}\sum_{i=1}^{D}num_k\end{matrix} n=∑i=1Dnumk,聚合神经网络参数 N t + 1 = ∑ i = 1 ∣ c ∣ M N t + 1 i / n N_{t+1}=\begin{matrix}\sum_{i=1}^{|c|}MN_{t+1}^i/n\end{matrix} Nt+1=∑i=1∣c∣MNt+1i/n



其中SMC加密过程计算如下,以物品嵌入为例,在聚合的过程中 I R i j 加减的随机矩阵被抵消了,也就是每个用户的参数加减了一个全局和为零的分量 IR_{ij}加减的随机矩阵被抵消了,也就是每个用户的参数加减了一个全局和为零的分量 IRij加减的随机矩阵被抵消了,也就是每个用户的参数加减了一个全局和为零的分量:



Experiments
作者的实验很多,可以大致看下,看看作者在提出方法后都使用哪些实验来丰富论文。
Evaluation settings
- 作者使用了四个数据进行实验,分别为:MovieLens 100k and MovieLens 1M, Lastfm 2k and Foursquare New York (NY)。
- 作者使用最大最小值和数据量的方差和标准差来衡量统计异构(non-iid)。
- 作者采用留一评估法,并且每个正样本采集100个负样本。即在排名时使用1个正样本与100个负样本之间的排名。
- 作者使用HR@K和NDCG@K来评估推荐器的性能。


Implementation details
- 作者使用了pytorch实现,但没有代码。
- 初始化权重使用Xavier进行初始化,在pytorch就是这个
nn.init.xavier_uniform_。 - 共同超参数。潜在因子数量
D=12,MLP的隐藏层共4层h={48,24,12,6}。 - 每个正样本对应
4个负样本。 - 所有参数使用BCE loss 和 Adam跟新,学习率为
0.001,总体训练400轮,每轮中用户本地训练epoch=1。 - 每轮参与者数量
c从{10,20,50,100,200,300,|P|}进行搜索。其中20,120,50,50个参与者比较好。
Aggregation function impact
本小节主要验证MF-FedAvg、FedAvg和SimlpeAvg不同聚合方法对收敛速度和模型效率的影响。这里自然是本文提出的方法更好。


Data federation impact
本小节作者主要用于验证数据异构对推荐模型的影响。
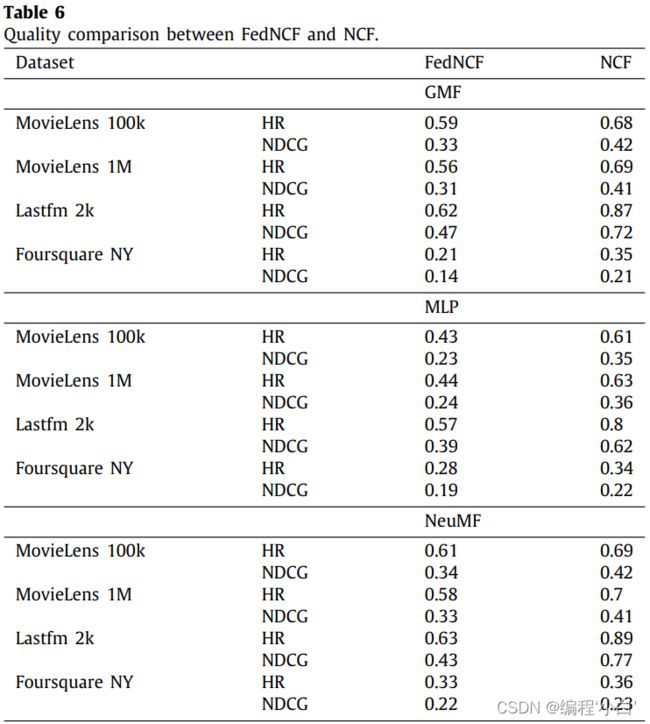
\qquad 与GMF相比,FedMLP和FedNeuMF模型在联邦训练开始时提高了收敛性。然而,FedNeuMF和FedGMF在每个数据集的训练迭代结束时都能提供相似的推荐质量,而FedMLP不能收敛。
\qquad FedMLP的这种行为可以归因于FL的分布式特性。在集中式环境中,MLP模型试图捕捉给定用户配置文件的用户之间的相似性,以提供更高质量的推荐。然而,在我们的设置中,用户概要文件从未被传输,因此,相关性无法充分了解。在FedMLP中,每个用户只拥有其相应的用户向量,因此,每次训练迭代都会导致全局学习目标的不一致,从而阻止收敛。因此,内部同时包含GMF和MLP模型的NeuMF算法利用了MLP模型在训练迭代开始时的快速收敛,然后利用GMF的小步骤提供高质量的推荐。尽管FedNeuMF提供了比FedGMF更好的推荐,在下一节中,我们认为在联邦设置中不适合使用复杂的体系结构,因为像MF这样的简单模型可以提供高质量的推荐,而不会产生沉重的计算开销。
Efficiency comparison
计算开销对比:
\qquad 通过测量浮点数来评估客户端上考虑的三个模型的效率操作(flop)和本地训练后需要传输到协调服务器进行聚合的参数的大小。flop的数量显示了用于本地训练的客户端设备的计算开销,而参数的大小显示了引入的通信开销。
每个模型的计算需求随着局部观测的数量线性增长。例如,MovieLens 100k和1M数据集中观察到的实例的最小数量是20。注意,在训练过程中,观察值随着负反馈的增长而增长。由于两个数据集包含一个具有相同观察数的用户,因此所需的最小flop是相同的(3200)。GMF模型的平均计算成本分别是FedMLP和FedNeuMF的89和90倍。GMF的计算效率还体现在需要传输聚合参数的大小上。模型的参数随项目配置文件中项目的数量线性增长,而GMF对用于聚合的传输参数的大小有较少的通信要求。更准确地说,GMF需要传输的参数几乎是对应的NeuMF模型的一半。
\qquad 将GMF模型与传统MF模型进行比较,所需要的flop数量几乎相等。GMF模型执行用户和物品向量的元素相乘,并将结果提交给单个处理单元,该处理单元使用sigmoid函数进一步转换。传统的MF模型对用户和物品的向量进行点积运算。因此,与MF相比,GMF的额外计算成本只涉及局部轮廓中每个项目的sigmoid函数的最终转换。类似地,为聚合传输的参数数量几乎相同。GMF模型的附加参数只涉及处理单元的权重和偏置。在经过考虑的设置下,与传统MF相比,GMF模型只需要13个额外的浮点值,即0.1 kB。基于对三种考虑的模型的计算成本、通信成本和推荐质量的观察,我们认为,简单技术比复杂模型更可取,因为它们简单,至少在涉及低资源的移动设备的联邦设置中是这样。与混合NeuMF相比,GMF模型提供了几乎相同的关于考虑的度量的建议,并且不会在客户端产生很高的计算和通信成本。因此,在具有较高计算资源(如桌面)的设备上,优先使用NeuMF和复杂模型,而在资源较低的设备上可以有效训练简单模型。因此,我们在联邦CF中确定了质量和复杂性之间的权衡,即在联邦设置中采用复杂模型是不简单的,因为总体计算成本可能令人望而却步。未来,我们计划评估其他协同过滤算法的推荐质量,并衡量推荐和计算成本之间的权衡。

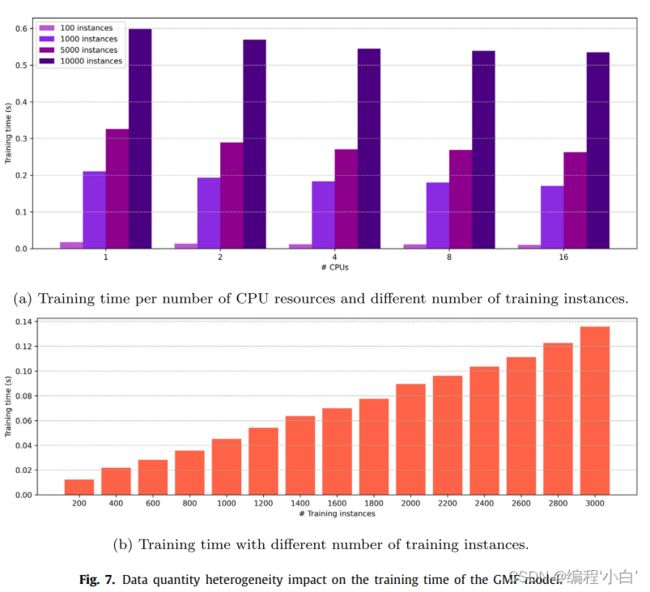
Heterogeneity impact
\qquad 在图7中,报告了不同数据和数据量的异质性对GMF模型训练时间的影响。我们通过考虑{1,2,4,8,16}CPU内核来考虑五种资源情况,通过考虑{100,1000,5000,10 000}实例来考虑四种本地数据集的大小情况。在最坏的情况下,考虑使用一个CPU 10,000个观测值,训练过程在不到一秒的时间内完成,而使用16个CPU核,训练速度加快10%。一般情况下,随着局部数据集大小的增加,计算时间变长,而系统的异构性对计算时间影响不大。仔细观察训练实例数量的影响,可以观察到训练时间随局部观察数的增加而线性增加。例如,2000个样本的计算时间为0.089≈2(0.045),其中0.045是使用5000个实例的训练时间。根据这些观察,联邦过程可能受到每个客户端训练数据量的严重影响,应该进一步研究,以为广义联邦学习提供收敛保证。
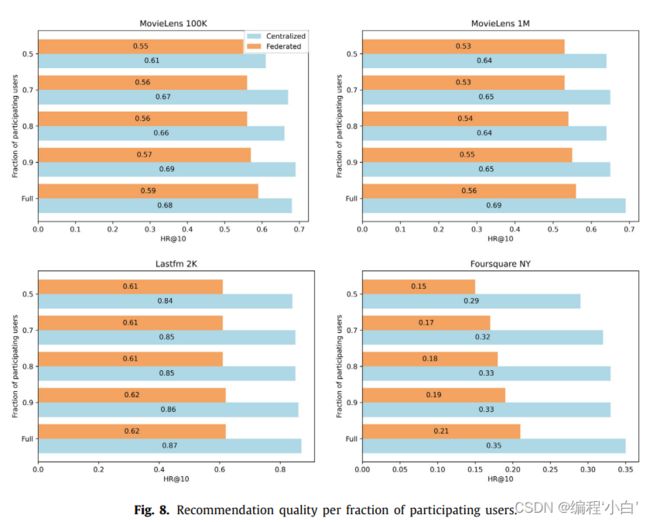
Number of participants impact
\qquad 在本节中,将评估关于参与训练过程的用户数量的集中式和联邦设置的鲁棒性。我们从{0.9,0.8,0.7,0.5}中随机选择一个用户子集参与计算,并删除每个数据集中其余的用户。注意,我们还排除了结束时没有交互的项冷启动问题在CF中被视为一个不同的任务。我们从头开始训练GMF模型,通过随机选择每个数据集参与计算的用户,重复实验5次。
平均结果如图8所示。通过删除参与的客户端,推荐质量几乎与原始设置相同。在集中式和联邦设置中,删除用户后质量会有小幅下降,分别在3%-7%和1%-6%之间。因此,两种技术中的最终模型对参与者的数量保持健壮性。更具体地说,随着用户数量的增加,推荐的质量也会提高。考虑到额外的训练迭代可以进一步在联邦设置中产生更好的建议,并且该技术应用于集中式环境中不可用的数据,可以认为在大规模部署的情况下,FL有超越传统模型的潜力。
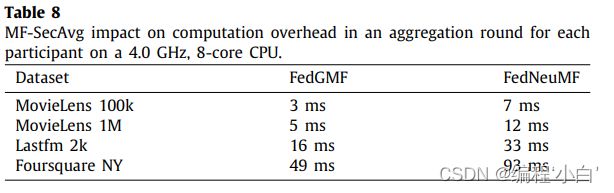
Secure aggregation impact
\qquad 使用MFSecAvg对随机生成矩阵的操作(图3,步骤2和3)将生成与普通聚合方法等效的聚合参数。因此,这个实验的目的是了解引入的计算开销。我们选择FedGMF和FedNeuMF模型进行实验,因为它们分别包含了NCF方法的最小和最大模型。表8显示了在全局轮询后初始化随机权值并在FedGMF和FedNeuMF模型中生成掩码权值所需的平均额外时间。注意,随机种子的协议阶段还有额外的通信成本,但可以忽略不计,如[16]中所述。
额外的计算成本取决于每个数据集中包含的项的数量。在最大的数据集(Foursquare NY)上,使用NeuMF模型的开销只涉及额外93毫秒的计算时间。因此,很容易观察到MF-SecAvg协议对计算开销。这表明,将MFSecAvg集成到联邦推荐系统中,在保护参与者隐私的同时,可以提供较高的计算效率和通信效率。
Conclusion
\qquad 神经协同过滤生成高质量推荐。尽管FL使参与者能够建立独立的模型而不暴露其原始数据,但私有交互仍然可以通过计算的输出泄露给协调机构。为了克服这一挑战,我们提出了一种隐私保护的方法,采用SecAvg协议[16]来满足潜在因素模型的更新过程。我们评估了FedNCF的推荐质量和效率,并讨论了所使用的聚合函数的影响。我们的实验证明了FL在推荐系统中的可行性,并支持来自低资源计算节点的少量贡献(数据保持在本地)可以产生高质量的机器学习模型的概念。改进FL的一个关键未来方向是进一步关注其安全性和隐私分析。尽管由于数据局部性,FL比集中式学习提供了更高的隐私级别,但对信息泄漏的正式估计是至关重要的。虽然[16]等安全聚合协议可以在单轮中确保参与者的隐私,但跨多轮的隐私保证仍然是一个有待解决的问题。