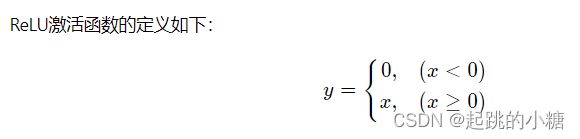02.计算机视觉（上）

• 卷积（Convolution）
• 池化（Pooling）
• ReLU激活函数
• 批归一化（Batch Normalization）
• 丢弃法（Dropout）

 a.卷积算子应用举例

（1）黑白边界检测,使用Conv2D算子

设置宽度方向的卷积核为[1,0,−1][1, 0, -1][1,0,−1]，此卷积核会将宽度方向间隔为1的两个像素点的数值相减。当卷积核在图片上滑动时，如果它所覆盖的像素点位于亮度相同的区域，则左右间隔为1的两个像素点数值的差为0。

 

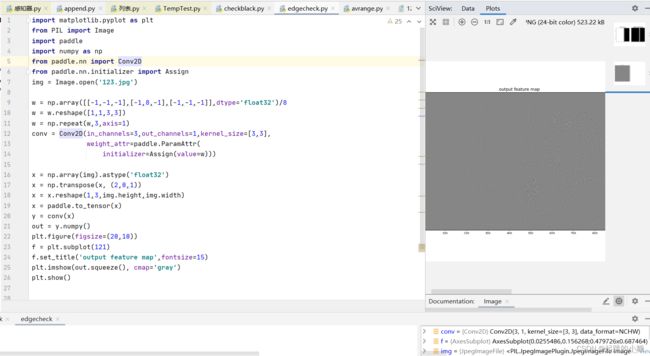
(2）边缘检测

卷积核(3*3卷积核的中间值是8，周围一圈的值是8个-1)对其进行操作，用来检测物体的外形轮廓，观察输出特征图跟原图之间的对应关系

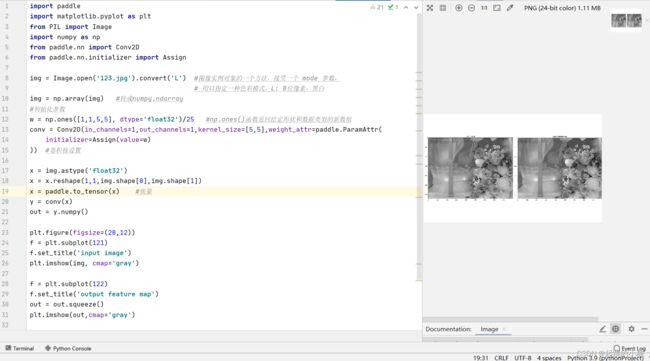
（3）均值模糊

卷积核（5*5的卷积核中每个值均为1）是用当前像素跟它邻域内的像素取平均，这样可以使图像上噪声比较大的点变得更平滑

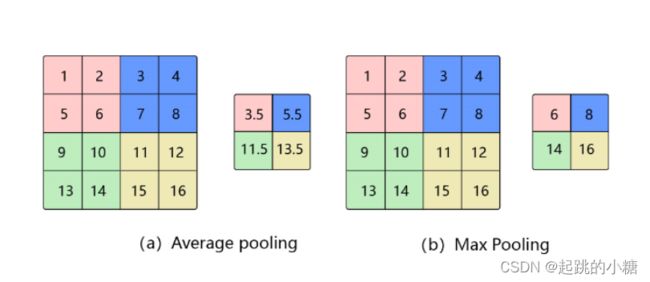
 b.池化（Pooling）

池化是使用某一位置的相邻输出的总体统计特征代替网络在该位置的输出，其好处是当输入数据做出少量平移时，经过池化函数后的大多数输出还能保持不变。

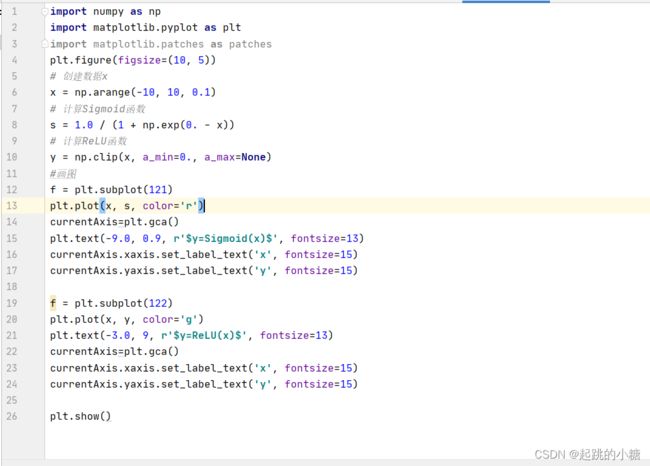
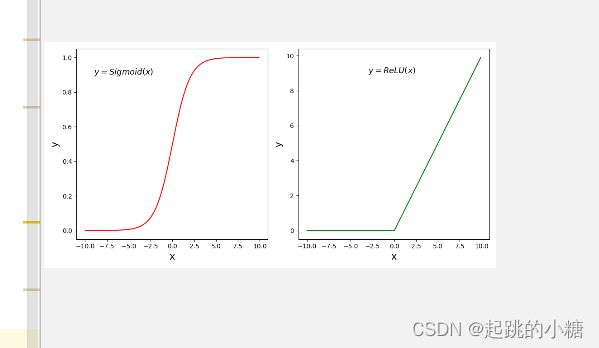
c.ReLU激活函数

 

 

 

 d.批归一化（Batch Normalization）

目的是对神经网络中间层的输出进行标准化处理，使得中间层的输出更加稳定。

1.计算均值

2.计算方差

3. 计算标准化之后的输出

示例一： 当输入数据形状是[N,K][N, K][N,K]时，一般对应全连接层的输出，示例代码如下所示。

这种情况下会分别对K的每一个分量计算N个样本的均值和方差，数据和参数对应如下：

输入 x, [N, K]     输出 y, [N, K]    均值 μB\mu_BμB​，[K, ]

方差 σB2\sigma_B^2σB2​, [K, ]     缩放参数γ\gammaγ, [K, ]

平移参数β\betaβ, [K, ]

# 输入数据形状是 [N, K]时的示例
import numpy as np
import paddle
from paddle.nn import BatchNorm1D
# 创建数据
data = np.array([[1,2,3], [4,5,6], [7,8,9]]).astype('float32')
# 使用BatchNorm1D计算归一化的输出
# 输入数据维度[N, K]，num_features等于K
bn = BatchNorm1D(num_features=3)
x = paddle.to_tensor(data)
y = bn(x)
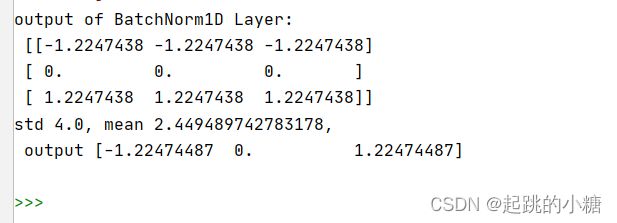
print('output of BatchNorm1D Layer: \n {}'.format(y.numpy()))

# 使用Numpy计算均值、方差和归一化的输出
# 这里对第0个特征进行验证
a = np.array([1,4,7])
a_mean = a.mean()
a_std = a.std()
b = (a - a_mean) / a_std
print('std {}, mean {}, \n output {}'.format(a_mean, a_std, b))

结果：

 示例二： 当输入数据形状是[N,C,H,W]时

import numpy as np
import paddle
from paddle.nn import BatchNorm2D
# 设置随机数种子
np.random.seed(100)
# 创建数据
data = np.random.rand(2,3,3,3).astype('float32')
# 使用BatchNorm2D计算归一化的输出
bn = BatchNorm2D(num_features=3)
x = paddle.to_tensor(data)
y = bn(x)
print('input of BatchNorm2D Layer: \n {}'.format(x.numpy()))
print('output of BatchNorm2D Layer: \n {}'.format(y.numpy()))

# 取出data中第0通道的数据，
# 使用numpy计算均值、方差及归一化的输出
a = data[:, 0, :, :]
a_mean = a.mean()
a_std = a.std()
b = (a - a_mean) / a_std
print('channel 0 of input data: \n {}'.format(a))
print('std {}, mean {}, \n output: \n {}'.format(a_mean, a_std, b))

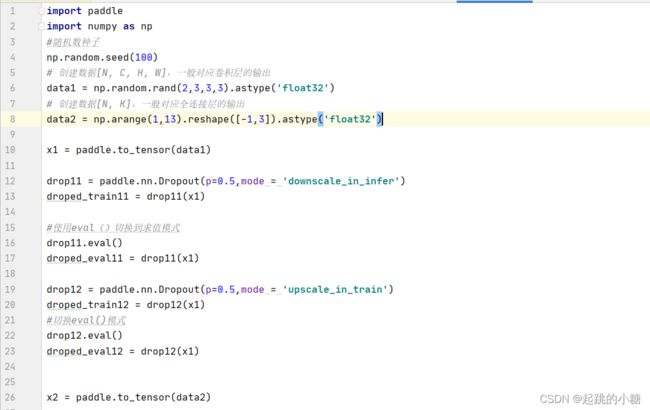
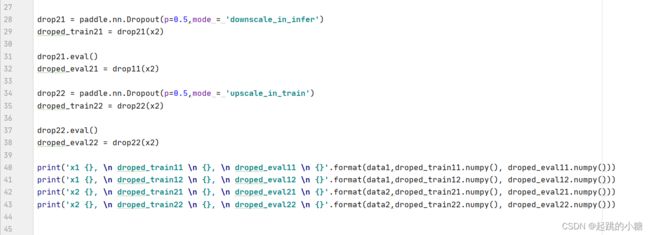
e.丢弃法

在神经网络学习过程中，随机删除一部分神经元。训练时，随机选出一部分神经元，将其输出设置为0，这些神经元将不对外传递信号。

• downscale_in_infer

训练时以比例rrr随机丢弃一部分神经元，不向后传递它们的信号；预测时向后传递所有神经元的信号，但是将每个神经元上的数值乘以 (1−r)(1 - r)(1−r)。

• upscale_in_train

训练时以比例rrr随机丢弃一部分神经元，不向后传递它们的信号，但是将那些被保留的神经元上的数值除以 (1−r)(1 - r)(1−r)；预测时向后传递所有神经元的信号，不做任何处理。

• p (float) ：将输入节点置为0的概率，即丢弃概率，默认值：0.5。该参数对元素的丢弃概率是针对于每一个元素而言，而不是对所有的元素而言。举例说，假设矩阵内有12个数字，经过概率为0.5的dropout未必一定有6个零。

• mode(str) ：丢弃法的实现方式，有'downscale_in_infer'和'upscale_in_train'两种，默认是'upscale_in_train'。

 

 结果：

 

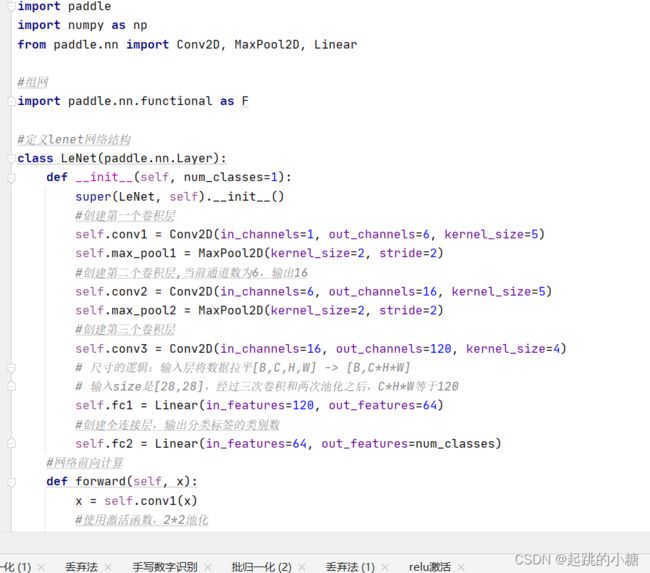
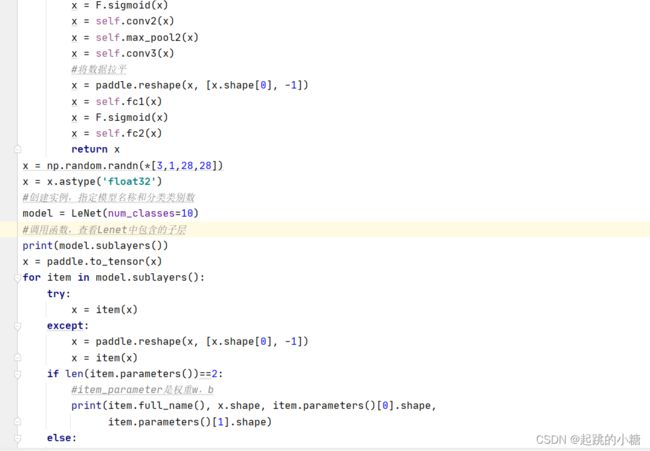
 LeNet手写数字识别