苏神文章解析(6篇)
苏神文章解析
文章目录
- 苏神文章解析
-
- 1.浅谈Transformer的初始化、参数化与标准化
-
- 1.1采样分布:截尾正态分布
- 1.2 正交初始化:Xavier初始化
- 1.3 直接标准化
- 1.4 NTK参数化
- 1.5 残差连接
- 2.模型参数的初始化
-
- 2.1 总结
- 2.2 为啥要正交初始化
- 2.3 Xavier初始化
- 2.4 考虑激活函数
- 3.BN为什么起作用
-
- 3.1 简述
- 3.2 具体推导
- 4. 花式Mask预训练(我悟了)
-
- 4.1 单向语言模型
- 4.2 Transformer专属
- 4.3 乱序语言模型
- 4.4 Seq2Seq
- 4.5 实验
- 4.6 总结
- 5. 词向量与Embedding究竟是怎么回事(有空补)
- 6. 《Attention is All You Need》浅读(有空补)
1.浅谈Transformer的初始化、参数化与标准化
《浅谈Transformer的初始化、参数化与标准化》
1.1采样分布:截尾正态分布
一般情况下,我们都是从指定均值和方差的随机分布中进行采样来初始化。其中常用的随机分布有三个:正态分布(Normal)、均匀分布(Uniform)和截尾正态分布(Truncated Normal)

一般来说,正态分布的采样结果更多样化一些,但它理论上是无界的,如果采样到绝对值过大的结果可能不利于优化;相反均匀分布是有界的,但采样结果通常更单一。于是就出现了结合两者优点的“截尾正态分布”。

1.2 正交初始化:Xavier初始化
从第二节可以得出结论:不考虑激活函数的情况下,正交初始化比较好界定。考虑激活函数得情况就比较麻烦。relu函数可以从N(0,1/2m)采样来初始化W。如果是是其它激活函数,分期起来比较麻烦甚至做不到完全正交初始化。那么可以考虑的方案是微调激活函数(激活函数进行各种变换)
详情见第二节
1.3 直接标准化
相比上一节各种“微调”,更直接的处理方法是各种Normalization方法,如Batch Normalization、Instance Normalization、Layer Normalization等,这类方法直接计算当前数据的均值方差来将输出结果标准化,而不用事先估计积分,有时候我们也称其为“归一化”。
这三种标准化方法大体上都是类似的,除了Batch Normalization多了一步滑动平均预测用的均值方差外,它们只不过是标准化的维度不一样。比如NLP尤其是Transformer模型用得比较多就是Layer Normalization是:
Normalization一般都包含了减均值(center)和除以标准差(scale)两个部分,但近来的一些工作逐渐尝试去掉center这一步,甚至有些工作的结果显示去掉center这一步后性能还略有提升。
比如2019年的论文《Root Mean Square Layer Normalization》比较了去掉center后的Layer Normalization,文章称之为RMS Norm。论文总的结果显示:RMS Norm比Layer Normalization更快,效果也基本一致。
比如2019年的论文《Root Mean Square Layer Normalization》比较了去掉center后的Layer Normalization,文章称之为RMS Norm。
一个直观的猜测是,center操作,类似于全连接层的bias项,储存到的是关于数据的一种先验分布信息,而把这种先验分布信息直接储存在模型中,反而可能会导致模型的迁移能力下降。所以T5不仅去掉了Layer Normalization的center操作,它把每一层的bias项也都去掉了。
1.4 NTK参数化
- Xavier初始化是用“均值为0、方差为1/m的随机分布”初始化。
- NTK参数化:用“均值为0、方差为1的随机分布”来初始化,但是将输出结果除以 m \sqrt{m} m。高斯过程中被称为“NTK参数化”
NTK参数化跟直接用Xavier初始化相比,有什么好处吗?
理论上,利用NTK参数化后,所有参数都可以用方差为1的分布初始化,这意味着每个参数的量级大致都是相同的O(1)级别,于是我们可以设置较大的学习率,比如 1 0 − 2 10^{−2} 10−2,并且如果使用自适应优化器,其更新量大致是 梯 度 梯 度 ⨂ 梯 度 × 学 习 率 \frac{梯度}{\sqrt{梯度\bigotimes 梯度}}\times 学习率 梯度⨂梯度梯度×学习率,那么我们就知道 1 0 − 2 10^{−2} 10−2的学习率每一步对参数的调整程度大致是1%。
总的来说,NTK参数化能让我们更平等地处理每一个参数,并且比较形象地了解到训练的更新幅度,以便我们更好地调整参数。
为什么Attention中除以 d \sqrt{d} d这么重要?
对于两个d维向量q,k,假设它们都采样自“均值为0、方差为1”的分布,那么它们的内积的二阶矩是: E [ ( q , k ) ] 2 = d E[(q,k)]^{2}=d E[(q,k)]2=d。由于均值也为0,所以这也意味着方差也是d。
Attention是内积后softmax,主要设计的运算是 e q ⋅ k e^{q⋅k} eq⋅k,我们可以大致认为内积之后、softmax之前的数值在 − 3 d -3\sqrt{d} −3d到 3 d 3\sqrt{d} 3d这个范围内,由于d通常都至少是64,所以 e 3 d e^{3\sqrt{d}} e3d比较大而 e − 3 d e^{-3\sqrt{d}} e−3d比较小,因此经过softmax之后,Attention的分布非常接近一个one hot分布了,这带来严重的梯度消失问题,导致训练效果差。
相应地,解决方法就有两个:
- 像NTK参数化那样,在内积之后除以 d \sqrt{d} d,使q⋅k的方差变为1,对应 e 3 e^3 e3, e − 3 e^{−3} e−3都不至于过大过小,这样softmax之后也不至于变成one hot而梯度消失了,这也是常规的Transformer如BERT里边的Self Attention的做法
- 另外就是不除以 d \sqrt{d} d,但是初始化q,k的全连接层的时候,其初始化方差要多除以一个d,这同样能使得使q⋅k的初始方差变为1,T5采用了这样的做法。
1.5 残差连接
2.模型参数的初始化
《从几何视角来理解模型参数的初始化策略》
2.1 总结
| 条件 | 初始化 |
|---|---|
| m=n | Xavier初始化:从N(0,1/n)采样来初始化W |
m| 无法做到正交初始化 |
|
| m≥n | 从N(0,1/m)采样来初始化W |
| tanh激活函数 | Xavier初始化直接适用于tanh激活 |
| relu激活函数 | 从N(0,1/2m)采样来初始化W |
2.2 为啥要正交初始化
对于复杂模型来说,参数的初始化显得尤为重要。糟糕的初始化,很多时候已经不单是模型效果变差的问题了,还更有可能是模型根本训练不动或者不收敛。在深度学习中常见的自适应初始化策略是Xavier初始化。
深度学习模型本身上就是一个个全连接层的嵌套,所以为了使模型最后的输出不至于在初始化阶段就过于“膨胀”或者“退化”,一个想法就是让模型在初始化时能保持模长不变。
正交矩阵是指满足 W ⊤ W = I W^⊤W=I W⊤W=I的矩阵,也就是说它的逆等于转置。正交矩阵的重要意义在于它在变换过程中保持了向量的模长不变.用数学公式来表达,就是设 W ∈ R n × n W\in \mathbb{R}^{n\times n} W∈Rn×n是一个正交矩阵,而 x ∈ R n x\in \mathbb{R}^{n} x∈Rn是任意向量,则x的模长等于 W x W_{x} Wx的模长:
∥ W x ∥ 2 = x T W T W x = x T x = x \left \| W_{x} \right \|^{2}=x^{T}W^{T}Wx=x^{T}x=x ∥Wx∥2=xTWTWx=xTx=x
这个想法形成的一个自然的初始化策略就是“以全零初始化b,以随机正交矩阵初始化W”
2.3 Xavier初始化
推论1: 高维空间中的任意两个随机向量几乎都是垂直的
推论2: 从N(0,1/n)中随机选取 n 2 n^2 n2个数,组成一个n×n的矩阵,这个矩阵近似为正交矩阵,且n越大,近似程度越好。
推论3: 从任意的均值为0、方差为1/n的分布p(x)中独立重复采样出来的n×n矩阵,都接近正交矩阵。
Xavier初始化:从N(0,1/n)采样来初始化W。从推论2可以看出,从N(0,1/n)采样而来的n×n矩阵就已经接近正交矩阵了。这种初始化也叫Glorot初始化,作者叫Xavier Glorot~
此外,采样分布也不一定是N(0,1/n),前面推论3说了你可以从任意均值为0、方差为1/n的分布中采样。
上面说的是输入和输出维度都是n的情况,如果输入是n维,输出是m维呢?这时候 W ∈ R m × n W\in \mathbb{R}^{m\times n} W∈Rm×n,保持Wx模长不变的条件依然是 W ⊤ W = I W^⊤W=I W⊤W=I。
- m
- 推论四:当m≥n时,从任意的均值为0、方差为1/m的分布p(x)中独立重复采样出来的m×n矩阵,近似满足 W ⊤ W = I W^⊤W=I W⊤W=I(只需要把采样分布的方差改为1/m就好)。

sigmoid函数:W服从 U [ − 96 n i + n i + 1 , 96 n i + n i + 1 ] U[-\sqrt{\frac{96}{n_{i}+n_{i+1}}},\sqrt{\frac{96}{n_{i}+n_{i+1}}}] U[−ni+ni+196,ni+ni+196]
Relu函数:W服从 U [ − 12 n i + n i + 1 , 12 n i + n i + 1 ] U[-\sqrt{\frac{12}{n_{i}+n_{i+1}}},\sqrt{\frac{12}{n_{i}+n_{i+1}}}] U[−ni+ni+112,ni+ni+112]
2.4 考虑激活函数
以上都是没有考虑激活函数得场景,考虑激活函数有:
- tanh(x) 在x比较小的时候有tanh(x)≈x,所以可以认为 Xavier初始化直接适用于tanh激活;
- relu时可以认为relu(y)会有 大约一半的元素被置零,所以模长大约变为原来的 1 2 \frac{1}{\sqrt{2}} 21,而要保持模长不变,可以让W乘上 2 \sqrt{2} 2,也就是说初始化方差从1/m变成2/m
事实上很难针对每一个激活函数都做好方差的调整,所以一个更通用的做法就是直接在激活函数后面加上一个类似Layer Normalization的操作,直接显式地恢复模长。这时候就轮到各种Normalization技巧登场了。
3.BN为什么起作用
《BN究竟起了什么作用?一个闭门造车的分析》
3.1 简述
BN在深度学习中可以加速训练,甚至有一定的抗过拟合作用,还允许我们用更大的学习率。因为BN使得整个损失函数的landscape更为平滑,从而使得我们可以更平稳地进行训练。
BN降低了神经网络的梯度的L常数,从而使得神经网络的学习更加容易,比如可以使用更大的学习率。而降低梯度的L常数,直观来看就是让损失函数没那么“跌宕起伏”,也就是使得landscape更光滑的意思了。(归一化、L常数请参考《深度学习中的Lipschitz约束:泛化与生成模型》)
推导:
- 假设f(θ)是损失函数,满足L约束。可以推导出梯度下降更新公式:
Δ θ = − η ∇ θ f ( θ ) ( 4 ) Δθ=−η∇θf(θ)(4) Δθ=−η∇θf(θ)(4)
代入不等式2得出:保证损失函数下降,要么学习率η 足够小,要不就要L足够小。 - 神经网络中激活函数是非线性的。根据柯西不等式得出:降低L的最直接方式是降低 ∣ E x ∼ p ( x ) [ x ⊗ x ] ∣ 1 ∣Ex∼p(x)[x⊗x]∣_{1} ∣Ex∼p(x)[x⊗x]∣1。
- 在不会明显降低原来神经网络拟合能力的前提下,降低这一项最好的办法就是对输入x进行变换,即平移和缩放。推出两个结论:
- 结论1: 将输入减去所有样本的均值,能降低梯度的L常数,是一个有利于优化又不降低神经网络拟合能力的操作
- 结论2: 缩放输入x最佳选择是除以标准差。这更像是一个自适应的学习率校正项,可以一定程度上消除了不同层级的输入对参数优化的差异性,使得整个网络的优化更为“同步”,或者说使得神经网络的每一层更为“平权”,从而更充分地利用好了整个神经网络,减少了在某一层过拟合的可能性。当然,如果输入的量级过大时,除以标准差这一项也有助于降低梯度的L常数。
3.2 具体推导
BN,也就是Batch Normalization,是当前深度学习模型(尤其是视觉相关模型)的一个相当重要的技巧,它能加速训练,甚至有一定的抗过拟合作用,还允许我们用更大的学习率,总的来说颇多好处(前提是你跑得起较大的batch size)
早期的解释主要是基于概率分布的,大概意思是将每一层的输入分布都归一化到N(0,1)上,减少了所谓的Internal Covariate Shift,从而稳定乃至加速了训练。
这种解释细思之下其实有问题的:不管哪一层的输入都不可能严格满足正态分布,从而单纯地将均值方差标准化无法实现标准分布N(0,1);其次,就算能做到N(0,1),这种诠释也无法进一步解释其他归一化手段(如Instance Normalization、Layer Normalization)起作用的原因。
2018年的论文《How Does Batch Normalization Help Optimization?》里边,作者明确地提出了上述质疑,否定了原来的一些观点,并提出了自己关于BN的新理解:BN主要作用是使得整个损失函数的landscape更为平滑,从而使得我们可以更平稳地进行训练。
核心不等式:

假设f(θ)是损失函数,而我们的目标是最小化f(θ)。我们自然希望f(θ)每一步都在下降,即 f ( θ + Δ θ ) < f ( θ ) f(θ+Δθ)
Δ θ = − η ∇ θ f ( θ ) ( 4 ) Δθ=−η∇θf(θ)(4) Δθ=−η∇θf(θ)(4)
这里η>0是一个标量,即学习率。式(4)就是梯度下降的更新公式,它是一个严格的不等式,所以它还可以告诉我们关于训练的一些结论。

BN是怎样炼成的 :
BN降低了神经网络的梯度的L常数,从而使得神经网络的学习更加容易,比如可以使用更大的学习率。而降低梯度的L常数,直观来看就是让损失函数没那么“跌宕起伏”,也就是使得landscape更光滑的意思了。
我们之前就讨论过L约束,之前我们讨论的是神经网络关于“输入”满足L约束,这导致了权重的谱正则和谱归一化,本文则是要讨论神经网络(的梯度)关于“参数”满足L约束,这导致了对输入的各种归一化手段,而BN是其中最自然的一种。
柯西不等式
探讨∇θf(θ)满足L约束的程度,并且探讨降低这个L的方法
结论:降低L常数最直接方法是,降低∣∣Ex∼p(x)[x⊗x]∣∣这一项(与参数无关)
式(12)的结果告诉我们,想办法降低L常数个做法就是对输入x进行变换,即平移和缩放。
结论1: 将输入减去所有样本的均值,能降低梯度的L常数,是一个有利于优化又不降低神经网络拟合能力的操作。(降低梯度的L常数前提是:必须不会明显降低原来神经网络拟合能力,否则只需要简单乘个0就可以让L降低到0了,但这并没有意义。)
如果一味追求更小的L,那直接σ→∞就好了,但这样的神经网络已经完全没有拟合能力了;但如果σ太小导致L过大,那又不利于优化。所以我们需要一个标准。
从公式可以看出:一个相对自然的选择是将σ取为输入的标准差。除以标准差更像是一个自适应的学习率校正项,它一定程度上消除了不同层级的输入对参数优化的差异性,使得整个网络的优化更为“同步”,或者说使得神经网络的每一层更为“平权”,从而更充分地利用好了整个神经网络,减少了在某一层过拟合的可能性。当然,如果输入的量级过大时,除以标准差这一项也有助于降低梯度的L常数。
4. 花式Mask预训练(我悟了)
本节选自苏剑林的文章:《从语言模型到Seq2Seq:Transformer如戏,全靠Mask》
背景
从Bert、GPT到XLNet等等,各种应用transformer结构的模型不断涌现,有基于现成的模型做应用的,有试图更好地去解释和可视化这些模型的,还有改进架构、改进预训练方式等以得到更好结果的。总的来说,这些以预训练为基础的工作层出不穷,有种琳琅满目的感觉
4.1 单向语言模型
语言模型可以说是一个无条件的文本生成模型(文本生成模型,可以参考《玩转Keras之seq2seq自动生成标题》)。单向语言模型相当于把训练语料通过下述条件概率分布的方式“记住”了:
p(x1,x2,x3,…,xn)=p(x1)p(x2|x1)p(x3|x1,x2)…p(xn|x1,…,xn−1)
我们一般说的“语言模型”,就是指单向的(更狭义的只是指正向的)语言模型。语言模型的关键点是要防止看到“未来信息”。如上式,预测x1的时候,是没有任何外部输入的;而预测x2的时候,只能输入x1,预测x3的时候,只能输入x1,x2;依此类推。
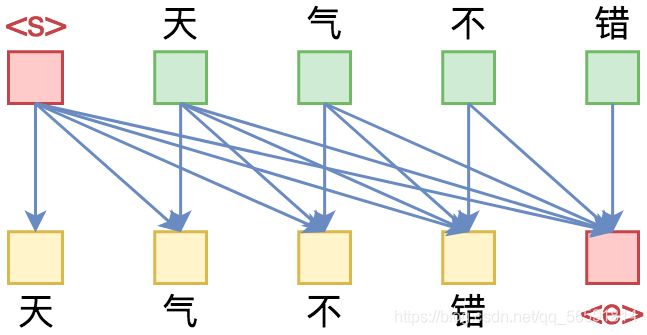
RNN模型是天然适合做语言模型的,因为它本身就是递归的运算;如果用CNN来做的话,则需要对卷积核进行Mask,即需要将卷积核对应右边的部分置零。如果是Transformer呢?那需要一个下三角矩阵形式的Attention矩阵,并将输入输出错开一位训练:

如图所示,Attention矩阵的每一行事实上代表着输出,而每一列代表着输入,而Attention矩阵就表示输出和输入的关联。假定白色方格都代表0,那么第1行表示“北”只能跟起始标记 < s > <s>相关了,而第2行就表示“京”只能跟起始标记 < s > <s>和“北”相关了,依此类推。((Mask的实现方式,也可以参考《“让Keras更酷一些!”:层中层与mask》)
4.2 Transformer专属
事实上,除了单向语言模型及其简单变体掩码语言模型之外,UNILM的Seq2Seq预训练、XLNet的乱序语言模型预训练,基本可以说是专为Transformer架构定制的。说白了,如果是RNN架构,根本就不能用乱序语言模型的方式来预训练。至于Seq2Seq的预训练方式,则必须同时引入两个模型(encoder和decoder),而无法像Transformer架构一样,可以一个模型搞定。
这其中的奥妙主要在Attention矩阵之上。Attention实际上相当于将输入两两地算相似度,这构成了一个 n 2 n^2 n2大小的相似度矩阵(即Attention矩阵,n是句子长度,本节的Attention均指Self Attention),这意味着它的空间占用量是O( n 2 n^2 n2)量级,相比之下,RNN模型、CNN模型只不过是O(n),所以实际上Attention通常更耗显存。
然而,有弊也有利,更大的空间占用也意味着拥有了更多的可能性,我们可以通过往这个O( n 2 n^2 n2)级别的Attention矩阵加入各种先验约束,使得它可以做更灵活的任务。说白了,也就只有纯Attention的模型,才有那么大的“容量”去承载那么多的“花样”。
而加入先验约束的方式,就是对Attention矩阵进行不同形式的Mask,这便是本文要关注的焦点。
4.3 乱序语言模型
乱序语言模型是XLNet提出来的概念,它主要用于XLNet的预训练上。
乱序语言模型跟语言模型一样,都是做条件概率分解,但是乱序语言模型的分解顺序是随机的:
p ( x 1 , x 2 , x 3 , … , x n ) = p ( x 1 ) p ( x 2 ∣ x 1 ) p ( x 3 ∣ x 1 , x 2 ) … p ( x n ∣ x 1 , x 2 , … , x n − 1 ) = p ( x 3 ) p ( x 1 ∣ x 3 ) p ( x 2 ∣ x 3 , x 1 ) … p ( x n ∣ x 3 , x 1 , … , x n − 1 ) = … = p ( x n − 1 ) p ( x 1 ∣ x n − 1 ) p ( x n ∣ x n − 1 , x 1 ) … p ( x 2 ∣ x n − 1 , x 1 , … , x 3 ) p(x1,x2,x3,…,xn) =p(x1)p(x2|x1)p(x3|x1,x2)…p(xn|x1,x2,…,xn−1) =p(x3)p(x1|x3)p(x2|x3,x1)…p(xn|x3,x1,…,xn−1) =… =p(xn−1)p(x1|xn−1)p(xn|xn−1,x1)…p(x2|xn−1,x1,…,x3) p(x1,x2,x3,…,xn)=p(x1)p(x2∣x1)p(x3∣x1,x2)…p(xn∣x1,x2,…,xn−1)=p(x3)p(x1∣x3)p(x2∣x3,x1)…p(xn∣x3,x1,…,xn−1)=…=p(xn−1)p(x1∣xn−1)p(xn∣xn−1,x1)…p(x2∣xn−1,x1,…,x3)
总之,x1,x2,…,xn任意一种“出场顺序”都有可能。原则上来说,每一种顺序都对应着一个模型,所以原则上就有n!个语言模型。而基于Transformer的模型,则可以将这所有顺序都做到一个模型中去!
实现某种特定顺序的语言模型,就将原来的下三角形式的Mask以某种方式打乱。正因为Attention提供了这样的一个n×n的Attention矩阵,我们才有足够多的自由度去以不同的方式去Mask这个矩阵,从而实现多样化的效果。
以“北京欢迎你”的生成为例,假设随机的一种生成顺序为“ < s > <s> → 迎 → 京 → 你 → 欢 → 北 → ”,那么我们只需要用下图中第二个子图的方式去Mask掉Attention矩阵,就可以达到目的了:

跟前面的单向语言模型类似,第4行只有一个蓝色格,表示“迎”只能跟起始标记 < s > <s>相关,而第2行有两个蓝色格,表示“京”只能跟起始标记 < s > <s>和“迎”相关,依此类推。直观来看,这就像是把单向语言模型的下三角形式的Mask“打乱”了。
有人会问,打乱后的Mask似乎没看出什么规律呀,难道每次都要随机生成一个这样的似乎没有什么明显概率的Mask矩阵?事实上有一种更简单的、数学上等效的训练方案,即在输入层面进行打乱。
纯Attention的模型本质上是一个无序的模型,它里边的词序实际上是通过Position Embedding加上去的。也就是说,我们输入的不仅只有token本身,还包括token所在的位置id;再换言之,你觉得你是输入了序列“[北, 京, 欢, 迎, 你]”,实际上你输入的是集合“{(北, 1), (京, 2), (欢, 3), (迎, 4), (你, 5)}”。
既然只是一个集合,跟顺序无关,那么我们完全可以换一种顺序输入,比如刚才的“ < s > <s>→ 迎 → 京 → 你 → 欢 → 北 → < e >
4.4 Seq2Seq
原则上来说,任何NLP问题都可以转化为Seq2Seq来做,它是一个真正意义上的万能模型。所以如果能够做到Seq2Seq,理论上就可以实现任意任务了。
微软的UNILM能将Bert与Seq2Seq优雅的结合起来。能够让我们直接用单个Bert模型就可以做Seq2Seq任务,而不用区分encoder和decoder。而实现这一点几乎不费吹灰之力——只需要一个特别的Mask。
UNILM直接将Seq2Seq当成句子补全来做。假如输入是“你想吃啥”,目标句子是“白切鸡”,那UNILM将这两个句子拼成一个:[CLS] 你 想 吃 啥 [SEP] 白 切 鸡 [SEP]。经过这样转化之后,最简单的方案就是训练一个语言模型,然后输入“[CLS] 你 想 吃 啥 [SEP]”来逐字预测“白 切 鸡”,直到出现“[SEP]”为止,即如下面的左图:
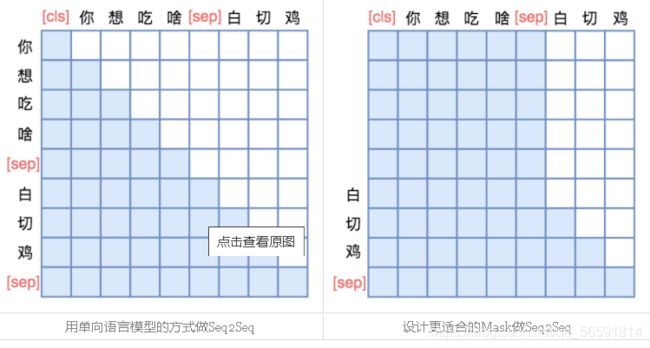
不过左图只是最朴素的方案,它把“你想吃啥”也加入了预测范围了(导致它这部分的Attention是单向的,即对应部分的Mask矩阵是下三角),事实上这是不必要的,属于额外的约束。真正要预测的只是“白切鸡”这部分,所以我们可以把“你想吃啥”这部分的Mask去掉,得到上面的右图的Mask。
UNILM单个Bert模型完成Seq2Seq任务的思路:
添加上述形状的Mask,输入部分的Attention是双向的,输出部分的Attention是单向,满足Seq2Seq的要求,而且没有额外约束。这样做不需要修改模型架构,并且还可以直接沿用Bert的Masked Language Model预训练权重,收敛更快。这符合“一Bert在手,天下我有”的万用模型的初衷,个人认为这是非常优雅的方案。
4.5 实验
事实上,上述的这些Mask方案,基本上都已经被集成在原作者写的bert4keras,读者可以直接用bert4keras加载bert的预训练权重,并且调用上述Mask方案来做相应的任务。具体UNILM实现例子,可以参考原文
4.6 总结
1.原始的seq2seq训练的是一个单向语言模型,语言模型的关键点是要防止看到“未来信息”。这一点可以通过循环神经网络的递归计算来实现,比如RNN。也可以通过CNN来做,只需要对卷积核进行Mask,即需要将卷积核对应右边的部分置零。如果是Transformer呢,那就需要一个下三角矩阵形式的Attention矩阵(表示输入与输出的关联)来实现。
2.不仅如此,通过Attention矩阵的不同Mask方式,还可以实现乱序语言模型和Seq2Seq。
前者只需要乱序原来的下三角形式的Masked-Attention矩阵(也等价于乱序输入序列),后者通过句子补全来做(类似输入一个词,预测接下来会输入的词,即输入法预测)。具体做的时候,只需要mask输入部分就行(感觉就是GPT2)。
3.之所以一个transformer结构能搞出后面那么多花样的玩法(Bert、GPT、XLNet等),关键在于Attention矩阵。Attention实际上相当于将输入两两地算相似度,这构成了一个 n 2 n^2 n2大小的相似度矩阵(复杂度O( n 2 n^2 n2))。比起RNN、CNN模型只是O(n),Attention通常更耗显存。
但正因如此,却也有了更多的可能性。通过往O( n 2 n^2 n2)级别的Attention矩阵加入各种先验约束,使得它可以做更灵活的任务。这种先验约束就是mask玩法。说白了,也就只有纯Attention的模型,才有那么大的“容量”去承载那么多的“花样”。(读到这里,我悟了)。
5. 词向量与Embedding究竟是怎么回事(有空补)
词向量与Embedding究竟是怎么回事
6. 《Attention is All You Need》浅读(有空补)
《Attention is All You Need》浅读(简介+代码)
RNN要逐步递归才能获得全局信息,因此一般要双向RNN才比较好;CNN事实上只能获取局部信息,是通过层叠来增大感受野;Attention的思路最为粗暴,它一步到位获取了全局信息:纯Attention!单靠注意力就可以。yt=f(xt,A,B)
Attention层的好处是能够一步到位捕捉到全局的联系,因为它直接把序列两两比较(代价是计算量变为 O ( n 2 ) O(n^2) O(n2),当然由于是纯矩阵运算,这个计算量相当也不是很严重);相比之下,RNN需要一步步递推才能捕捉到,而CNN则需要通过层叠来扩大感受野,这是Attention层的明显优势。