【深度学习】基本的反向传播准则

这其实是个一直想记录下来的问题，之前看到《深入浅出神经网络与深度学习》这本书中发现对此有一易懂的描述。结合最近跑的例程，来直观地回顾下。

在很多书的介绍中，都会将深度学习中的反向传播看作一个黑盒，使用者只需知道反向传播可用于权重的更新从而训练网络即可。但这种训练的基本机理本质其实构成了对神经网络本身的一种诠释，而这种诠释对于理解神经网络的适用性和拓展性恰恰是关键的，这也是本文决定对此展开的原因。

网络结构和参数定义

推导具体的反向传播机制前，先来给出网络结构的定义。

以一个简单的三层网络结构为例。第一层为输入层，这里假设有三个输入神经元； 第二层为隐藏层（或中间层），意味着网络在进行更复杂的特征特取操作，所谓深层网络，即有多层隐藏层的神经网络，网络的加深将提高其非线性表达能力； 第三层为输出层，这里输出的两个激活值将输入代价函数与预期值作比较输出误差结果。

在上节的感知机模型中，我们已经知晓了连接权重 $w$ 、偏置 $b$ 以及和激活函数 $\sigma$ 相对应的激活值 $a$ 所构成的基本方程。对于由多层感知机构成的神经网络来说，这个对于单个节点的方程仍旧是一致的。采用向量形式，我们将更简洁表达某层激活值的产生：

$$a_l=\sigma (w^l{a}^{l-1}+b^l)其中定义带权输入z^l=w^l{a}^{l-1}+b^l$$

即： 层与层间连接权重与上层激活值的点积加上该层的偏置将得到该层的带权输入$z^l$,而带权输入过激活函数就得到该层的激活值。

补充一个矩阵运算符号阿达马积或舒尔积$\odot$，这将后续简化方程的写法。

假设 $s$ 和 $t$ 是两个维度相同的向量，那么 $s\odot t$ 表示按元素的乘积，即$(s\odot t{)}_j=s_j{t}_j$

举例如下：

$$\left[\begin{array}{c}1\\ 2\end{array}\right]\odot \left[\begin{array}{c}3\\ 4\end{array}\right]=\left[\begin{array}{c}1\ast 3\\ 2\ast 4\end{array}\right]=\left[\begin{array}{c}3\\ 8\end{array}\right]$$

方程的推导

其实反向传播考量的是如何更改权重和偏置以控制代价函数，其终极含义就是计算偏导数$\partial C/\partial w_{jk}^l$ 和 $\partial C/\partial b_j^l$。一个具有启发性的认识——$\partial C/\partial z_j^l$ 是对神经元误差的度量（这里选择$z_j^l$表达误差是为后续方程形式的简化），即定义第 $l$ 层第 $j$ 个神经元上的误差 ${\delta }_j^l$ 定义为：
$${\delta }_j^l\equiv \frac{\partial C}{\partial z_j^l}$$

按照惯例，用${\delta }^l$ 表示与第 $l$ 层相关的误差向量。可以利用反向传播计算每一层 ${\delta }^l$，然后将这些误差与实际需要的量$\partial C/\partial w_{jk}^l$ 和 $\partial C/\partial b_j^l$ 关联起来。

在开始证明过程前，首先给出关于反向传播方程的四个式子，如下：

总结：反向传播方程

$${\delta }^L={\nabla }_{a}C\odot {\sigma }^{\prime }(z^L)输出层误差(1)$$

$${\delta }^l=((w^{l+1}{)}^T{\delta }^{l+1})\odot {\sigma }^{\prime }(z^l)前层传递误差(2)$$

$$\frac{\partial C}{\partial b_j^l}={\delta }_j^l偏置的变化率(3)$$

$$\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}{\delta }_j^l权重的变化率(4)$$

下面开始逐一证明，请记住核心的多元微积分链式法则。

（1）输出层误差

对于输出层误差，其定义为：
$${\delta }_j^L=\frac{\partial C}{\partial z_j^L}$$
其中，L为网络的层数，此即表明这是输出层第 j 个神经元上的误差。实际上，我们可以用输出激活值的偏导数形式重写以上的偏导数，即
$${\delta }_j^L=\sum _k\frac{\partial C}{\partial a_k^L}\frac{\partial a_k^L}{\partial z_j^L}$$
其中求和是对输出层的所有神经元进行的。当然，第 $k$ 个神经元的输出激活值 $a_k^L$ 只取决于 $k=j$ 时第 j 个神经元的输入权重 $z_j^L$ ，所以当 $k\ne j$ 时 $\partial a_k^L/\partial z_j^L$ 不存在（即无影响为0）。因此，方程可以化简为
$${\delta }_j^L=\frac{\partial C}{\partial a_j^L}\frac{\partial a_j^L}{\partial z_j^L}$$
这说明神经元的误差只与，损失函数对该神经元激活值的偏导 和 激活值对该神经元上的带权输入的偏导（此即激活函数在该点的导数值）有关。基于$a_j^L=\sigma (z_j^L)$，右边第2项就可以写成
$${\sigma }_j^L=\frac{\partial C}{\partial a_j^L}{\sigma }^{\prime }(z_j^L)$$
将上式扩展到输出层的每一个神经元，并用阿达马积表示，就可以得到（1）式的形式，即
$${\delta }^L={\nabla }_{a}C\odot {\sigma }^{\prime }(z^L)$$

（2）前层传递误差

这应该是最能说明反向传播算法中“反向”两字含义的式子，即从后向前传递了误差。具体来看，考虑的是用下一层误差${\delta }^{l+1}$的形式来表示误差${\delta }^l$。类似地，我们用${\delta }_k^{l+1}=\partial C/\partial z_k^{l+1}$重写${\delta }_j^l=\partial C/\partial z_j^l$。这同样可以用链式法则实现，即
$$\begin{array}{rl}{\delta }_j^l& =\frac{\partial C}{\partial z_j^l}\\ & =\sum _k\frac{\partial C}{\partial z_k^{l+1}}\frac{\partial z_k^{l+1}}{\partial z_j^l}\\ & =\sum _k\frac{\partial z_k^{l+1}}{\partial z_j^l}{\delta }_k^{l+1}\end{array}$$
最后一行交换了右边的两项，并代入了${\delta }_k^{l+1}$的定义，相应也就实现了代入下层误差。为了对最后一行求值，展开
$$z_k^{l+1}=\sum _j{w}_{kj}^{l+1}{a}_j^l+b_k^{l+1}=\sum _j{w}_{kj}^{l+1}\sigma \left(z_j^l\right)+b_k^{l+1}$$
对其求微分可得
$$\frac{\partial z_k^{l+1}}{\partial z_j^l}=w_{kj}^{l+1}{\sigma }^{\prime }\left(z_j^l\right)$$
将其反代回一开始的式子，就有
$${\delta }_j^l=\sum _k{w}_{kj}^{l+1}{\delta }_k^{l+1}{\sigma }^{\prime }\left(z_j^l\right)$$
这也就是（2）的分量形式，引入阿达马积的运算符后，可写出由后层向前层传递误差的向量形式，即
$${\delta }^l=((w^{l+1}{)}^T{\delta }^{l+1})\odot {\sigma }^{\prime }(z^l)$$

（3）偏置的变化率

类似前两步的证明，我们可以想到此时的证明仍旧是应用链式法则进行展开。考虑到
$${\delta }_j^l=\frac{\partial C}{\partial z_j^l}=\frac{\partial C}{\partial b_j^l}\frac{\partial b_j^l}{\partial z_j^l}$$
其中，可以将$z_j^l$展开
$$z_j^l=\sum _k{w}_{jk}^l{a}_k^{l-1}+b_j^l$$
两边同时对$b_j^l$求偏导，由于$w_{jk}^l$与$b_j^l$无关，因各自都是能够自由变化的变量。故
$$\frac{\partial z_j^l}{\partial b_j^l}=1$$
于是，就有（3）式的得证。
$$\frac{\partial C}{\partial b_j^l}={\delta }_j^l$$

（4）权重的变化率

与（3）中证明类似，我们有
$${\delta }_j^l=\frac{\partial C}{\partial z_j^l}=\frac{\partial C}{\partial w_{jk}^l}\frac{\partial w_{jk}^l}{\partial z_j^l}$$
同样，将$z_k^l$展开
$$z_j^l=\sum _k{w}_{jk}^l{a}_k^{l-1}+b_j^l$$
两边同时对$w_{jk}^l$求偏导，$w_{jk}^l$不仅与$b_j^l$无关，而且与其他的权重也无关，仅与它自身有关，于是就有：
$$\frac{\partial z_j^l}{\partial w_{jk}^l}=a_k^{l-1}$$
变换后，就有（4）式的得证
$$\frac{\partial C}{\partial w_{jk}^l}=a_k^{l-1}{\delta }_j^l$$

小结

通过上述证明过程，我们容易看出，我们是如何通过反向传播算法将误差逐层回传，并更新权重和偏置的数学原理。

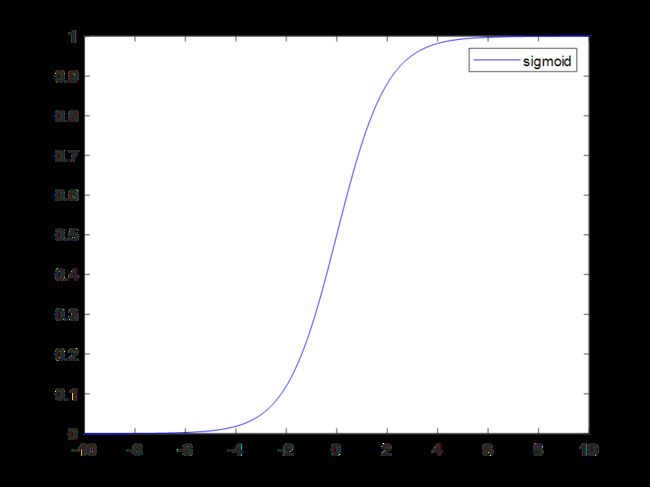
现在我们回看方程（1），在其分量形式中，看看其中的项 ${\sigma }^{\prime }(z_j^L)$。回顾一下sigmoid函数的图像，当 $\sigma (z_j^L)$近似为0或1时，sigmoid函数变得非常平缓，这时${\sigma }^{\prime }(z_j^l)\approx 0$ 。因此，如果输出神经元处于小激活值（约为0）或者大激活值（约为1）时，最终层的权重学习会非常缓慢，这时可以说输出神经元已经饱和，并且，权重学习也会终止（或者学习非常缓慢），输出神经元的偏置也与之类似。因为我们回看方程（3）和（4），可以发现权重和偏置的更新其实依赖于误差 $\sigma (z_j^l)$，而对于输出层而言，误差又如前所见依赖于激活函数的导数${\sigma }^{\prime }(z_j^L)$，于是在饱和状态下，学习就会变得困难。

我们最后来看（2），注意（2）中的项 ${\sigma }^{\prime }(z_j^l)$ ，这说明误差在向前层反向传递时，都会乘上一个激活函数的导数值。而对于sigmoid函数而言，可以知道这个导数值介于0~1之间，如果网络的层数很大，则由输出层向浅层传播时，我们可以知道误差将经过多次缩小，误差最终将会下降到忽略不计的程度（接近0），于是浅层的学习将变得十分困难，这就是梯度消失现象。

同样，与输出层神经元饱和情景下的分析一致，中间神经元的饱和也会导致 ${\delta }_j^l$变得很小，因为 ${\sigma }^{\prime }(z_j^l)$ 很小。即总结为：对于输入到已饱和神经元的任何权重都学习缓慢。

反向传播方程对于任何激活函数都是成立的， 这里忽略了对代价函数的讨论，因为那又是一块内容，但可以证明上述推断本身与任何具体的代价函数是无关的。同时我们可能已经有了新的想法，sigmoid函数在某些应用中可能并不适合作为理想的激活函数。而其实设计具有特定学习属性的激活函数实际上也是神经网络中的一块重要内容。

尝试观察

下面举一个简单的例子，说明如何在神经网络中具体观察权重迭代的更新，这是一个将神经网络用于非线性拟合的例子。

首先我们生成一个带噪声的正弦信号（非线性信号），如下：

x = torch.unsqueeze(torch.linspace(-np.pi, np.pi, 100), dim = 1) # 构建等差数列
y = torch.sin(x) + 0.5*torch.rand(x.size())  # 条件随机数

而后我们定义了一个网络结构：

class Net(nn.Module):  # 定义类，存储网络结构
    def __init__(self):
        super(Net, self).__init__()
        self.predict = nn.Sequential(
            nn.Linear(1,10),  # 全连接层，1个输入，10个输出
            nn.ReLU(),  #ReLU激活函数
            nn.Linear(10,1)  # 全连接层，10个输入，1个输出
        )

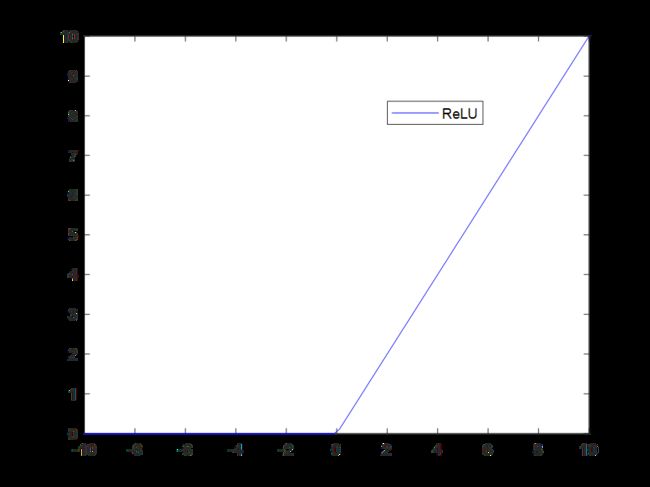
此处使用的激活函数是ReLU函数，与Sigmoid函数相比，ReLU在正区间内不会发生梯度消失问题，且函数求导比较简单，是在CNN网络中常用的激活函数。

在训练中我们通过调用modules，对层进行遍历即可获取全连接层所对应的权值，对应的代码如下：

        # 输出权重变化，net.modules返回的是generator类型
        for layer in net.modules():
            if isinstance(layer, nn.Linear):
                print(layer.weight)

全流程的代码如下：

# 这是一个用神经网络进行函数拟合的函数
import  numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt

x = torch.unsqueeze(torch.linspace(-np.pi, np.pi, 100), dim = 1) # 构建等差数列
y = torch.sin(x) + 0.5*torch.rand(x.size())  # 条件随机数

class Net(nn.Module):  # 定义类，存储网络结构
    def __init__(self):
        super(Net, self).__init__()
        self.predict = nn.Sequential(
            nn.Linear(1,10),  # 全连接层，1个输入，10个输出
            nn.ReLU(),  #ReLU激活函数
            nn.Linear(10,1)  # 全连接层，10个输入，1个输出
        )

    def forward(self,x):  # 定义前向传播过程
        prediction = self.predict(x)  # 将x传入网络
        return prediction


net = Net()
optimizer = torch.optim.SGD(net.parameters(), lr = 0.05)  # 设置优化器
loss_func = nn.MSELoss()  # 设置损失函数
plt.ion()   # 打开交互模式

for epoch in range(1000):
    out = net(x)   # 实际输出
    loss = loss_func(out, y)  # 实际输出和期望输出传入损失函数
    optimizer.zero_grad()  # 清除梯度
    loss.backward()  # 误差反向传播

    optimizer.step()  # 优化器开始优化
    if epoch % 25 == 0:  # 每25epoch显示
        plt.cla()   # 清除上一次绘图
        plt.scatter(x,y)  # 绘制散点图

        # 输出权重变化，net.modules返回的是generator类型
        for layer in net.modules():
            if isinstance(layer, nn.Linear):
                print(layer.weight)

        plt.plot(x, out.data.numpy(), 'r', lw = 5 )  # 绘制曲线图
        plt.text(0, 0 , f'loss={loss}',fontdict={'size':20,'color':'red'})  #  添加文字来显示loss值

        plt.pause(0.1) # 显示时间0.1s

    plt.show()

plt.ioff()  # 关闭交互模式
plt.show()  # 定格显示最后结果

可以看到图形界面上实时显示的拟合效果，伴随着损失值的下降，网络将逐渐拟合出正弦曲线的形状。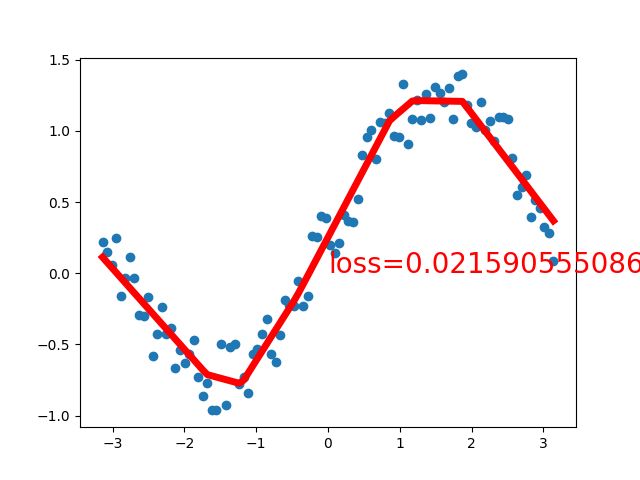

我们也可以在控制台看到输出的网络权重。这里截取了最后一次训练时得到的权重作为示例，可以看到分别是10×1（1→10）的一个权值矩阵和一个1×10（10→1）的权重矩阵，而这与之前定义的两个全连接层的网络结构正好是对应的。

---

参考：
《深入浅出神经网络与深度学习》作者: [澳]迈克尔·尼尔森 译者: 朱小虎 第2章
《Python神经网络入门与实战》作者: 王凯 第7章