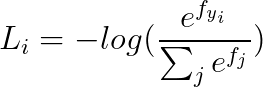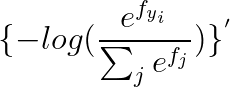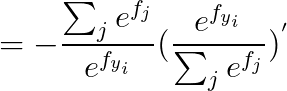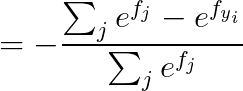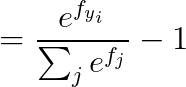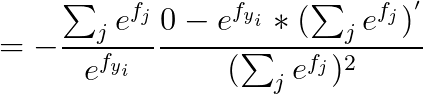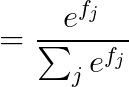【CS231n】Softmax浅谈 + Softmax代码实现
1. Softmax
1.1 Softmax概要
Softmax分类器可以认为是在SVM分类器的基础上做了一些改进,SVM的输出为对于一张image在各个类别上面的评分,因为没有明确的参照,所以很难直接解释。而Softmax则不同,Softmax将对于一张image在各个类别上面的评分看作为归一化的对数概率,概率给了我们明确的参照,我们可以认为这张image应该认为是概率最高所对应的类别。
1.2 Softmax VS SVM
SVM认为只要在正确分类上面的得分高出其它类别Δ就不会对损失产生任何贡献,而Softmax却认为在概率归一化以后在正确类别上面的概率大于其它类别上面的概率。
SVM鼓励我们在正确类别上面的得分高出其它类别的得分Δ,Softmax鼓励我们在正确类别上的概率(归一化后)趋于1。
2. Loss Fuction
2.1 cross-entropy loss
2.2 calculus
2.2.1 当 j == yi :
2.2.2 当 j != yi
3. 代码实现
github:https://github.com/GIGpanda/CS231n
代码由两个文件组成,一个叫softmax.py, 另一个也叫softmax.py
3.1 softmax.py(整体框架)
3.1.1 数据预处理
# softmax
from __future__ import print_function
import random
import numpy as np
from cs231n.data_utils import load_CIFAR10
import matplotlib.pyplot as plt
from cs231n.classifiers.softmax import softmax_loss_naive
import time
from cs231n.gradient_check import grad_check_sparse
from cs231n.classifiers.softmax import softmax_loss_vectorized
from cs231n.classifiers import Softmax
plt.rcParams['figure.figsize'] = (10.0, 8.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
def get_CIFAR10_data(num_training=49000, num_validation=1000, num_test=1000, num_dev=500):
"""
Load the CIFAR-10 dataset from disk and perform preprocessing to prepare
it for the linear classifier. These are the same steps as we used for the
SVM, but condensed to a single function.
"""
# Load the raw CIFAR-10 data
cifar10_dir = 'cs231n/datasets/cifar-10-batches-py'
X_train, y_train, X_test, y_test = load_CIFAR10(cifar10_dir)
# subsample the data
mask = list(range(num_training, num_training + num_validation))
X_val = X_train[mask]
y_val = y_train[mask]
mask = list(range(num_training))
X_train = X_train[mask]
y_train = y_train[mask]
mask = list(range(num_test))
X_test = X_test[mask]
y_test = y_test[mask]
mask = np.random.choice(num_training, num_dev, replace=False)
X_dev = X_train[mask]
y_dev = y_train[mask]
# Preprocessing: reshape the image data into rows
X_train = np.reshape(X_train, (X_train.shape[0], -1))
X_val = np.reshape(X_val, (X_val.shape[0], -1))
X_test = np.reshape(X_test, (X_test.shape[0], -1))
X_dev = np.reshape(X_dev, (X_dev.shape[0], -1))
# Normalize the data: subtract the mean image
mean_image = np.mean(X_train, axis=0)
X_train -= mean_image
X_val -= mean_image
X_test -= mean_image
X_dev -= mean_image
# add bias dimension and transform into columns
X_train = np.hstack([X_train, np.ones((X_train.shape[0], 1))])
X_val = np.hstack([X_val, np.ones((X_val.shape[0], 1))])
X_test = np.hstack([X_test, np.ones((X_test.shape[0], 1))])
X_dev = np.hstack([X_dev, np.ones((X_dev.shape[0], 1))])
return X_train, y_train, X_val, y_val, X_test, y_test, X_dev, y_dev
# Cleaning up variables to prevent loading data multiple times (which may cause memory issue)
try:
del X_train, y_train
del X_test, y_test
print('Clear previously loaded data.')
except:
pass
# Invoke the above function to get our data.
X_train, y_train, X_val, y_val, X_test, y_test, X_dev, y_dev = get_CIFAR10_data()
print('Train data shape: ', X_train.shape)
print('Train labels shape: ', y_train.shape)
print('Validation data shape: ', X_val.shape)
print('Validation labels shape: ', y_val.shape)
print('Test data shape: ', X_test.shape)
print('Test labels shape: ', y_test.shape)
print('dev data shape: ', X_dev.shape)
print('dev labels shape: ', y_dev.shape)3.1.2 计算Softmax loss、grad并验证
# First implement the naive softmax loss function with nested loops.
# Open the file cs231n/classifiers/softmax.py and implement the
# softmax_loss_naive function.
# Generate a random softmax weight matrix and use it to compute the loss.
W = np.random.randn(3073, 10) * 0.0001
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0)
# As a rough sanity check, our loss should be something close to -log(0.1).
print('loss: %f' % loss)
print('sanity check: %f' % (-np.log(0.1)))
# Complete the implementation of softmax_loss_naive and implement a (naive)
# version of the gradient that uses nested loops.
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 0.0)
# As we did for the SVM, use numeric gradient checking as a debugging tool.
# The numeric gradient should be close to the analytic gradient.
f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 0.0)[0]
grad_numerical = grad_check_sparse(f, W, grad, 10)
# similar to SVM case, do another gradient check with regularization
loss, grad = softmax_loss_naive(W, X_dev, y_dev, 5e1)
f = lambda w: softmax_loss_naive(w, X_dev, y_dev, 5e1)[0]
grad_numerical = grad_check_sparse(f, W, grad, 10)3.1.3 向量化计算loss、grad,并且比较两种计算方式的时间开销
# Now that we have a naive implementation of the softmax loss function and its gradient,
# implement a vectorized version in softmax_loss_vectorized.
# The two versions should compute the same results, but the vectorized version should be
# much faster.
tic = time.time()
loss_naive, grad_naive = softmax_loss_naive(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('naive loss: %e computed in %fs' % (loss_naive, toc - tic))
tic = time.time()
loss_vectorized, grad_vectorized = softmax_loss_vectorized(W, X_dev, y_dev, 0.000005)
toc = time.time()
print('vectorized loss: %e computed in %fs' % (loss_vectorized, toc - tic))
# As we did for the SVM, we use the Frobenius norm to compare the two versions
# of the gradient.
grad_difference = np.linalg.norm(grad_naive - grad_vectorized, ord='fro')
print('Loss difference: %f' % np.abs(loss_naive - loss_vectorized))
print('Gradient difference: %f' % grad_difference)3.1.4 交叉验证
# Use the validation set to tune hyperparameters (regularization strength and
# learning rate). You should experiment with different ranges for the learning
# rates and regularization strengths; if you are careful you should be able to
# get a classification accuracy of over 0.35 on the validation set.
results = {}
best_val = -1
best_softmax = None
learning_rates = [1e-7, 5e-7]
regularization_strengths = [2.5e4, 5e4]
################################################################################
# TODO: #
# Use the validation set to set the learning rate and regularization strength. #
# This should be identical to the validation that you did for the SVM; save #
# the best trained softmax classifer in best_softmax. #
################################################################################
# Your code
for lr in learning_rates:
for reg in regularization_strengths:
results[(lr, reg)] = []
num_iters = 1500
for lr in learning_rates:
for reg in regularization_strengths:
softmax = Softmax()
softmax.train(X_train, y_train, learning_rate=lr, reg=reg, num_iters=num_iters)
y_train_pred = softmax.predict(X_train)
train_accuracy = np.mean(y_train_pred == y_train)
y_val_pred = softmax.predict(X_val)
val_accuracy = np.mean(y_val_pred == y_val)
results[(lr, reg)] = (train_accuracy, val_accuracy)
if best_val < val_accuracy:
best_val = val_accuracy
best_softmax = softmax
################################################################################
# END OF YOUR CODE #
################################################################################
# Print out results.
for lr, reg in sorted(results):
train_accuracy, val_accuracy = results[(lr, reg)]
print('lr %e reg %e train accuracy: %f val accuracy: %f' % (
lr, reg, train_accuracy, val_accuracy))
print('best validation accuracy achieved during cross-validation: %f' % best_val)
# evaluate on test set
# Evaluate the best softmax on test set
y_test_pred = best_softmax.predict(X_test)
test_accuracy = np.mean(y_test == y_test_pred)
print('softmax on raw pixels final test set accuracy: %f' % (test_accuracy, ))
# Visualize the learned weights for each class
w = best_softmax.W[:-1, :] # strip out the bias
w = w.reshape(32, 32, 3, 10)
w_min, w_max = np.min(w), np.max(w)
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
for i in range(10):
plt.subplot(2, 5, i + 1)
# Rescale the weights to be between 0 and 255
wimg = 255.0 * (w[:, :, :, i].squeeze() - w_min) / (w_max - w_min)
plt.imshow(wimg.astype('uint8'))
plt.axis('off')
plt.title(classes[i])
plt.show()3.2 softmax.py(计算loss、grad)
3.2.1 用循环计算loss、grad
import numpy as np
from random import shuffle
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
num_train = X.shape[0]
num_classes = W.shape[1]
scores = X.dot(W)
logc = np.max(scores, axis=1)
logc = np.reshape(np.repeat(logc, num_classes), scores.shape)
expscores = np.exp(scores+logc)
for i in range(num_train):
expmom = sum(expscores[i])
expson = expscores[i, y[i]]
loss += -np.log(expson / expmom)
for j in range(num_classes):
if j != y[i]:
dW[:, j] += (expscores[i][j] / expmom) * X[i]
else :
dW[:, y[i]] += ((expscores[i][y[i]] / expmom) - 1) * X[i]
loss /= num_train
loss += 0.5 * reg * np.sum(W*W)
dW /= num_train
dW += reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW3.2.2 向量化计算loss、grad
def softmax_loss_vectorized(W, X, y, reg):
"""
Softmax loss function, vectorized version.
Inputs and outputs are the same as softmax_loss_naive.
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
#############################################################################
# TODO: Compute the softmax loss and its gradient using no explicit loops. #
# Store the loss in loss and the gradient in dW. If you are not careful #
# here, it is easy to run into numeric instability. Don't forget the #
# regularization! #
#############################################################################
num_train = X.shape[0]
num_classes = W.shape[1]
scores = X.dot(W)
logc = np.max(scores, axis=1)
logc = np.reshape(np.repeat(logc, num_classes), scores.shape)
scores += logc
expscores = np.exp(scores)
expmom = np.sum(expscores, axis=1)
expson = expscores[np.arange(num_train), y]
loss += np.sum(-(np.log(expson / expmom)))
loss /= num_train
loss += 0.5 * reg * np.sum(W*W)
expmom = np.reshape(np.repeat(expmom, num_classes), expscores.shape)
M = expscores / expmom
M[np.arange(num_train), y] -= 1
# !!! M[:, y] -= 1 wrong why ?
dW = X.T.dot(M)
dW /= num_train
dW += reg * W
#############################################################################
# END OF YOUR CODE #
#############################################################################
return loss, dW