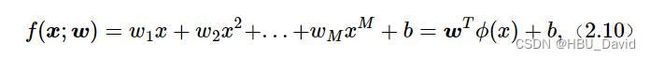NNDL 实验三 线性回归

目录

前言

2.2 线性回归

2.2.1 数据集构建

2.2.2 模型构建

2.2.3 损失函数

2.2.4 模型优化

2.2.5 模型训练 

2.2.6 模型评估 

2.2.7 样本数量 & 正则化系数 

2.3 多项式回归

2.3.1 数据集构建

2.3.2 模型构建

2.3.3 模型训练 

  2.3.4 模型评估

2.4 Runner类介绍

2.5 基于线性回归的波士顿房价预测

        2.5.1 数据处理

        2.5.2 模型构建

        2.5.3 完善Runner类 

        2.5.4 模型训练 

3.5 模型测试 

3.6 模型预测 

总结

---

前言

本文主要是利用pytorch实现简单的数据集构建，以及对数据集进行线性模型的构建

---

2.2 线性回归

2.2.1 数据集构建

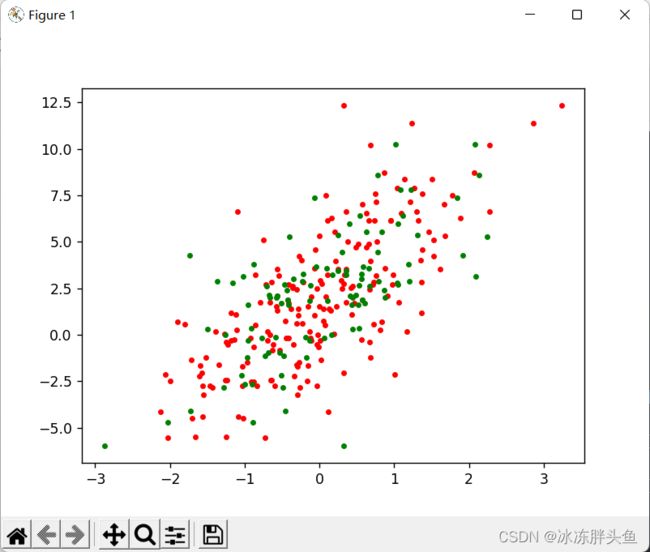
构造一个小的回归数据集：

生成 150 个带噪音的样本，其中 100 个训练样本，50 个测试样本，并打印出训练数据的可视化分布。

import torch
import matplotlib.pyplot as plt
def creat_data(w,b,num):
    #随机生成均值为0,标准差为1的（num,len(w))）张量
    x=torch.normal(0,1,(num,len(w)))
    #对生成的x求出对应的y
    y=torch.matmul(x,w)+b
    #添加噪音
    y+=torch.normal(0,0.01,y.shape)
    return x,y
#生成数据集
data_x,data_y=creat_data(torch.tensor([2.0,3.0]),2,150)
#训练集
data_x_train,data_y_train=data_x[0:100],data_y[0:100]
#测试集
data_x_test,data_y_test=data_x[100:150],data_y[100:150]
plt.figure(1)
plt.plot(data_x_train,data_y_train,'.r',data_x_test,data_y_test,'.g')
plt.show()

 

2.2.2 模型构建

接下来，我们必须定义模型，将模型的输入和参数同模型的输出关联起来。 回想一下，要计算线性模型的输出， 我们只需计算输入特征X和模型权重w的矩阵-向量乘法后加上偏置b。 注意，上面的Xw是一个向量，而b是一个标量。 

# 初始化模型参数
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
def linreg(X, w, b):
    # 线性回归模型
    return np.dot(X, w) + b

2.2.3 损失函数

回归任务中常用的评估指标是均方误差

均方误差（mean-square error, MSE）是反映估计量与被估计量之间差异程度的一种度量。

 

def squared_loss(y_hat, y):
    # 均方损失
    return (y_hat - y.reshape(y_hat.shape)) ** 2

【注意：代码实现中没有除2】思考：没有除2合理么？谈谈自己的看法，写到实验报告。 

没有除2是合理的，损失函数是反映预测值和真实值之间的差距程度，除以2不会对差距产生影响，只是为了消除计算平方项变导数出现的2. 

2.2.4 模型优化

经验风险 （ Empirical Risk ），即在训练集上的平均损失。

在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。 接下来，朝着减少损失的方向更新我们的参数。 下面的函数实现小批量随机梯度下降更新。 该函数接受模型参数集合、学习速率和批量大小作为输入。每 一步更新的大小由学习速率lr决定。 因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size） 来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。

def sgd(params, lr, batch_size):
    # 小批量随机梯度下降
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

 思考1. 为什么省略了1/N不影响效果？

答：1/N是一个常数， 在反向传播求偏导时 ，对于相同的超参数只会影响收敛速度，并不会最终收敛的结果

思考 2. 什么是最小二乘法 （ Least Square Method ， LSM ）

答：最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合。其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。
最小二乘法同梯度下降类似，都是一种求解无约束最优化问题的常用方法，并且也可以用于曲线拟

2.2.5 模型训练 

现在我们已经准备好了模型训练所有需要的要素，可以实现主要的训练过程部分了。 理解这段代码至关重要，因为从事深度学习后， 你会一遍又一遍地看到几乎相同的训练过程。 在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。 计算完损失后，我们开始反向传播，存储每个参数的梯度。 最后，我们调用优化算法sgd来更新模型参数。

lr = 0.03
num_epochs = 5
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, X_train, y_train):
        l = loss(X_train * w + b, y_train)  # X和y的小批量损失
        # 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()
        sgd([w, b], lr, batch_size)  # 使用参数的梯度更新参数
    with torch.no_grad():
        train_l = loss(net(features, w, b), labels)
        print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
 print(w, b)

epoch 1, loss 1.037590
epoch 2, loss 0.361732
epoch 3, loss 0.128096
epoch 4, loss 0.046069 

w的估计误差: tensor([0.2005, 0.2956], grad_fn=)
b的估计误差: tensor([0.0554], grad_fn=) 

2.2.6 模型评估 

用训练好的模型预测一下测试集的标签，并计算在测试集上的损失。

y_predict = linreg(features, w, b)
loss_test = squared_loss(y_predict, labels)
loss = 0
for i in loss_test:
    loss += i
print(loss/50)

tensor([0.1391], grad_fn=) 

2.2.7 样本数量 & 正则化系数 

（1） 调整训练数据的样本数量，由 100 调整到 5000，观察对模型性能的影响。

运行结果：

w_pred tensor([[0.9998][1.9876]], requires_grad=True)
b_pred tensor([0.5213], requires_grad=True)
loss 0.000050

可以看到，训练集数据增多之后，预测出的w和b的值更接近真实值。

（2） 调整正则化系数，观察对模型性能的影响。

optimizer = torch.optim.SGD(model.parameters(),0.01,weight_decay=0.1)

2.3 多项式回归

 2.3.1 数据集构建

构建训练和测试数据，其中：

训练数样本 15 个，测试样本 10 个，高斯噪声标准差为 0.1，自变量范围为 (0,1)。

import math
import torch
import matplotlib.pyplot as plt
import numpy as np
# sin函数: sin(2 * pi * x)
def sin(x):
    y =torch.sin(2 * math.pi * x)
    return y
def create_toy_data(func, interval, sample_num, noise = 0.0, add_outlier = False, outlier_ratio = 0.001):
    # 均匀采样
    # 使用torch.rand在生成sample_num个随机数
    X = torch.rand(size = [sample_num]) * (interval[1]-interval[0]) + interval[0]
    y = func(X)
 
    # 生成高斯分布的标签噪声
    # 使用torch.normal生成0均值，noise标准差的数据
    epsilon = torch.tensor(np.random.normal(0,noise,size=y.shape[0]))
    y = y + epsilon
    if add_outlier:     # 生成额外的异常点
        outlier_num = int(len(y)*outlier_ratio)
        if outlier_num != 0:
            # 使用torch.randint生成服从均匀分布的、范围在[0, len(y))的随机Tensor
            outlier_idx = torch.rand(len(y),shape = [outlier_num])
            y[outlier_idx] = y[outlier_idx] * 5
    return X, y
func = sin
interval = (0,1)
train_num = 15
test_num = 10
noise = 0.5 #0.1
X_train, y_train = create_toy_data(func=func, interval=interval, sample_num=train_num, noise = noise)
X_test, y_test = create_toy_data(func=func, interval=interval, sample_num=test_num, noise = noise)
 
X_underlying = torch.linspace(interval[0],interval[1],steps=100)
y_underlying = sin(X_underlying)
 
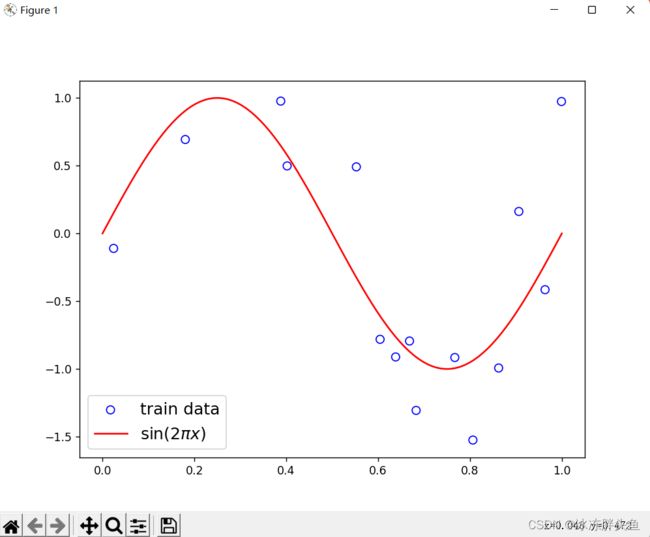
# 绘制图像
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
#plt.scatter(X_test, y_test, facecolor="none", edgecolor="r", s=50, label="test data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.legend(fontsize='x-large')
plt.savefig('ml-vis2.pdf')
plt.show()
 

 运行结果:

2.3.2 模型构建

套用求解线性回归参数的方法来求解多项式回归参数

import  torch
# 多项式转换
def polynomial_basis_function(x, degree=2):
 
    if degree == 0:
        return torch.ones(shape=x.shape, dtype=torch.float32)
 
    x_tmp = x
    x_result = x_tmp
 
    for i in range(2, degree + 1):
        x_tmp = torch.multiply(x_tmp, x)  # 逐元素相乘
        x_result = torch.concat((x_result, x_tmp), axis=-1)
 
    return x_result
 
 
# 简单测试
data = [[2], [3], [4]]
X = torch.as_tensor(data=data, dtype=torch.float32)
degree = 3
transformed_X = polynomial_basis_function(X, degree=degree)
print("转换前：", X)
print("阶数为", degree, "转换后：", transformed_X)
 
 

运行结果 

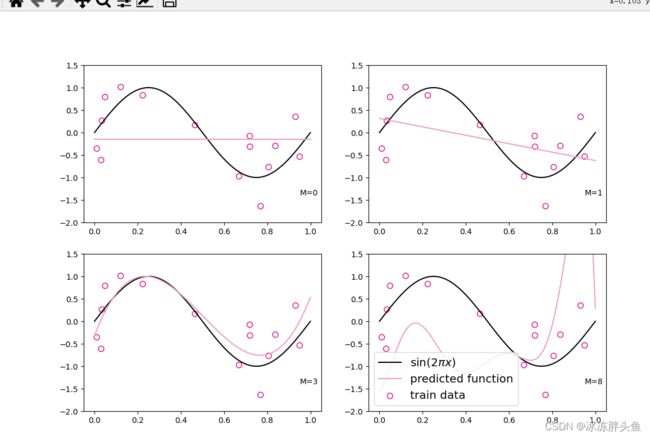
 2.3.3 模型训练

对于多项式回归，我们可以同样使用前面线性回归中定义的LinearRegression算子、训练函数train、均方误差函数mean_squared_error。

  for i, degree in enumerate([0, 1, 3, 8]):  # []中为多项式的阶数
    model = Linear(degree)
    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), degree)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), degree)
 
    model = optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))  # 拟合得到参数
 
    y_underlying_pred = model(X_underlying_transformed).squeeze()
 
    print(model.params)
 
    # 绘制图像
    plt.subplot(2, 2, i + 1)
    plt.scatter(X_train, y_train, facecolor="none", edgecolor='#e4007f', s=50, label="train data")
    plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
    plt.plot(X_underlying, y_underlying_pred, c='#f19ec2', label="predicted function")
    plt.ylim(-2, 1.5)
    plt.annotate("M={}".format(degree), xy=(0.95, -1.4))
 
# plt.legend(bbox_to_anchor=(1.05, 0.64), loc=2, borderaxespad=0.)
plt.legend(loc='lower left', fontsize='x-large')
plt.savefig('ml-vis3.pdf')
plt.show()

 

 

 2.3.4 模型评估

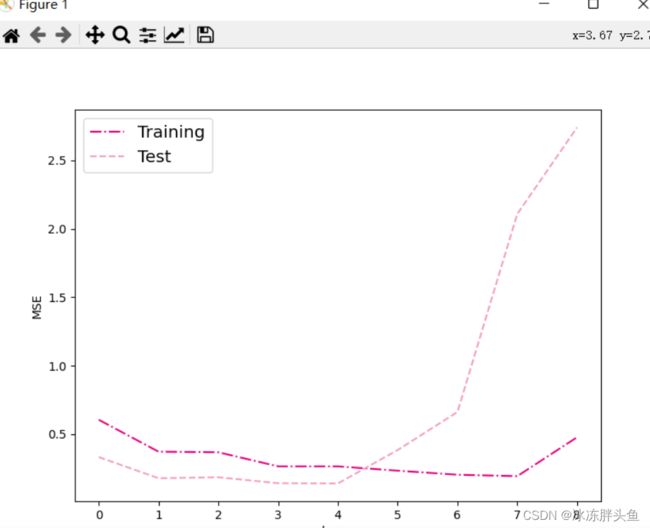
 通过均方误差来衡量训练误差、测试误差以及在没有噪音的加入下sin函数值与多项式回归值之间的误差，更加真实地反映拟合结果。多项式分布阶数从0到8进行遍历。

# 训练误差和测试误差
training_errors = []
test_errors = []
distribution_errors = []
 
# 遍历多项式阶数
for i in range(9):
    model = Linear(i)
 
    X_train_transformed = polynomial_basis_function(X_train.reshape([-1, 1]), i)
    X_test_transformed = polynomial_basis_function(X_test.reshape([-1, 1]), i)
    X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1, 1]), i)
 
    optimizer_lsm(model, X_train_transformed, y_train.reshape([-1, 1]))
 
    y_train_pred = model(X_train_transformed).squeeze()
    y_test_pred = model(X_test_transformed).squeeze()
    y_underlying_pred = model(X_underlying_transformed).squeeze()
 
    train_mse = mean_squared_error(y_true=y_train, y_pred=y_train_pred).item()
    training_errors.append(train_mse)
 
    test_mse = mean_squared_error(y_true=y_test, y_pred=y_test_pred).item()
    test_errors.append(test_mse)
 
    # distribution_mse = mean_squared_error(y_true=y_underlying, y_pred=y_underlying_pred).item()
    # distribution_errors.append(distribution_mse)
 
print("train errors: \n", training_errors)
print("test errors: \n", test_errors)
# print ("distribution errors: \n", distribution_errors)
 
# 绘制图片
plt.rcParams['figure.figsize'] = (8.0, 6.0)
plt.plot(training_errors, '-.', mfc="none", mec='#e4007f', ms=10, c='#e4007f', label="Training")
plt.plot(test_errors, '--', mfc="none", mec='#f19ec2', ms=10, c='#f19ec2', label="Test")
# plt.plot(distribution_errors, '-', mfc="none", mec="#3D3D3F", ms=10, c="#3D3D3F", label="Distribution")
plt.legend(fontsize='x-large')
plt.xlabel("degree")
plt.ylabel("MSE")
plt.savefig('ml-mse-error.pdf')
plt.show()

运行结果 

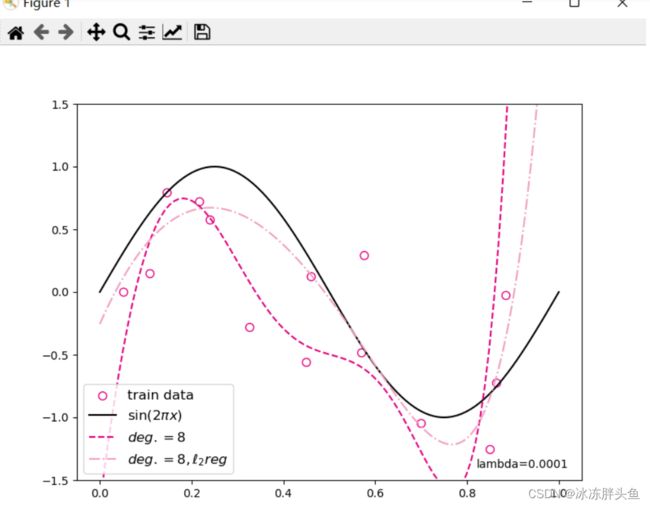
 对于模型过拟合的情况，可以引入正则化方法，通过向误差函数中添加一个惩罚项来避免系数倾向于较大的取值。

degree = 8 # 多项式阶数
reg_lambda = 0.0001 # 正则化系数
 
X_train_transformed = polynomial_basis_function(X_train.reshape([-1,1]), degree)
X_test_transformed = polynomial_basis_function(X_test.reshape([-1,1]), degree)
X_underlying_transformed = polynomial_basis_function(X_underlying.reshape([-1,1]), degree)
 
model = Linear(degree) 
 
optimizer_lsm(model,X_train_transformed,y_train.reshape([-1,1]))
 
y_test_pred=model(X_test_transformed).squeeze()
y_underlying_pred=model(X_underlying_transformed).squeeze()
 
model_reg = Linear(degree) 
 
optimizer_lsm(model_reg,X_train_transformed,y_train.reshape([-1,1]),reg_lambda=reg_lambda)
 
y_test_pred_reg=model_reg(X_test_transformed).squeeze()
y_underlying_pred_reg=model_reg(X_underlying_transformed).squeeze()
 
mse = mean_squared_error(y_true = y_test, y_pred = y_test_pred).item()
print("mse:",mse)
mes_reg = mean_squared_error(y_true = y_test, y_pred = y_test_pred_reg).item()
print("mse_with_l2_reg:",mes_reg)
 
# 绘制图像
plt.scatter(X_train, y_train, facecolor="none", edgecolor="#e4007f", s=50, label="train data")
plt.plot(X_underlying, y_underlying, c='#000000', label=r"$\sin(2\pi x)$")
plt.plot(X_underlying, y_underlying_pred, c='#e4007f', linestyle="--", label="$deg. = 8$")
plt.plot(X_underlying, y_underlying_pred_reg, c='#f19ec2', linestyle="-.", label="$deg. = 8, \ell_2 reg$")
plt.ylim(-1.5, 1.5)
plt.annotate("lambda={}".format(reg_lambda), xy=(0.82, -1.4))
plt.legend(fontsize='large')
plt.savefig('ml-vis4.pdf')
plt.show()
 

 运行结果：

（真的好多，人已经麻了） 

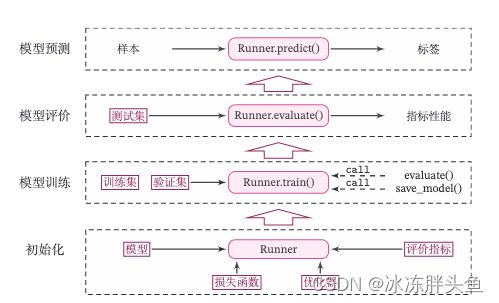
2.4 Runner类介绍

机器学习方法流程包括数据集构建、模型构建、损失函数定义、优化器、模型训练、模型评价、模型预测等环节。

为了更方便地将上述环节规范化，我们将机器学习模型的基本要素封装成一个Runner类。

除上述提到的要素外，再加上模型保存、模型加载等功能。

Runner类的成员函数定义如下：

1）__init__函数：实例化Runner类，需要传入模型、损失函数、优化器和评价指标等；

2）train函数：模型训练，指定模型训练需要的训练集和验证集；

3）evaluate函数：通过对训练好的模型进行评价，在验证集或测试集上查看模型训练效果；

4）predict函数：选取一条数据对训练好的模型进行预测；

5）save_model函数：模型在训练过程和训练结束后需要进行保存；

6）load_model函数：调用加载之前保存的模型。

class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        self.model = model         # 模型
        self.optimizer = optimizer # 优化器
        self.loss_fn = loss_fn     # 损失函数   
        self.metric = metric       # 评估指标
 
    # 模型训练
    def train(self, train_dataset, dev_dataset=None, **kwargs):
        pass
 
    # 模型评价
    def evaluate(self, data_set, **kwargs):
        pass
 
    # 模型预测
    def predict(self, x, **kwargs):
        pass
 
    # 模型保存
    def save_model(self, save_path):
        pass
 
    # 模型加载
    def load_model(self, model_path):
        pass
 

optimizer_lsm代码如下：

def optimizer_lsm(model, X, y, reg_lambda=0):
    N, D = X.shape
    # 对输入特征数据所有特征向量求平均
    x_bar_tran = torch.mean(X, axis=0).T
    # 求标签的均值,shape=[1]
    y_bar = torch.mean(y)
    # torch.subtract通过广播的方式实现矩阵减向量
    x_sub = torch.subtract(X, x_bar_tran)
    # 使用torch.all判断输入tensor是否全0
    if torch.all(x_sub == 0):
        model.params['b'] = y_bar
        model.params['w'] = torch.zeros([D])
        return model
    # torch.inverse求方阵的逆
    tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
                         reg_lambda * torch.eye(D))
 
    w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))
 
    b = y_bar - torch.matmul(x_bar_tran, w)
 
    model.params['b'] = b
    model.params['w'] = torch.squeeze(w, axis=-1)
 
    return model

 2.5 基于线性回归的波士顿房价预测

使用线性回归来对马萨诸塞州波士顿郊区的房屋进行预测。

实验流程主要包含如下5个步骤：

1）数据处理：包括数据清洗（缺失值和异常值处理）、数据集划分，以便数据可以被模型正常读取，并具有良好的泛化性;
2）模型构建：定义线性回归模型类；
3）训练配置：训练相关的一些配置，如：优化算法、评价指标等；
4）组装训练框架Runner：Runner用于管理模型训练和测试过程；
5）模型训练和测试：利用Runner进行模型训练和测试。

2.5.1 数据处理

 2.5.1.2 数据清洗

import pandas as pd # 开源数据分析和操作工具
 
# 利用pandas加载波士顿房价的数据集
data=pd.read_csv(r"boston_house_prices.csv")
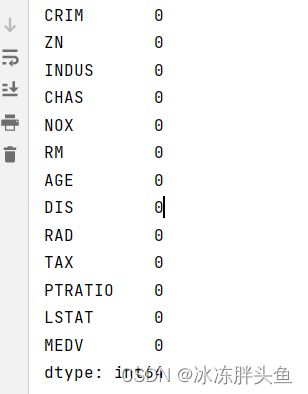
# 查看各字段缺失值统计情况
print(data.isna().sum())

运行结果 

 

由上面的结果可以知道，波士顿房价预测数据集中不存在缺失值的情况。
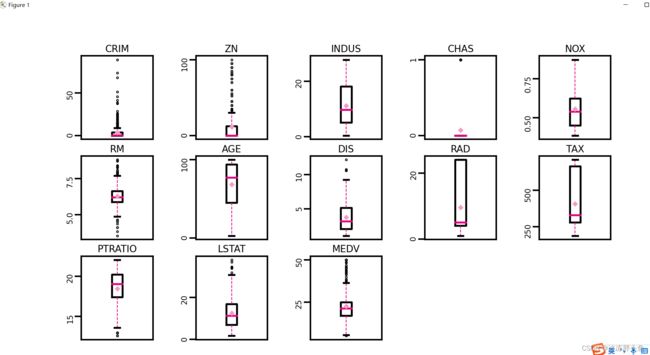
异常值处理:通过箱线图直观的显示数据分布，并观测数据中的异常值。箱线图一般由五个统计值组成：最大值、上四分位、中位数、下四分位和最小值。一般来说，观测到的数据大于最大估计值或者小于最小估计值则判断为异常值，其中：
最大估计值=上四分位+1.5∗(上四分位−下四分位)
最小估计值=下四分位−1.5∗(上四分位−下四分位)
 

import matplotlib.pyplot as plt # 可视化工具
 
# 箱线图查看异常值分布
def boxplot(data, fig_name):
    # 绘制每个属性的箱线图
    data_col = list(data.columns)
    
    # 连续画几个图片
    plt.figure(figsize=(5, 5), dpi=300)
    # 子图调整
    plt.subplots_adjust(wspace=0.6)
    # 每个特征画一个箱线图
    for i, col_name in enumerate(data_col):
        plt.subplot(3, 5, i+1)
        # 画箱线图
        plt.boxplot(data[col_name], 
                    showmeans=True, 
                    meanprops={"markersize":1,"marker":"D","markeredgecolor":'#f19ec2'}, # 均值的属性
                    medianprops={"color":'#e4007f'}, # 中位数线的属性
                    whiskerprops={"color":'#e4007f', "linewidth":0.4, 'linestyle':"--"},
                    flierprops={"markersize":0.4},
                    ) 
        # 图名
        plt.title(col_name, fontdict={"size":5}, pad=2)
        # y方向刻度
        plt.yticks(fontsize=4, rotation=90)
        plt.tick_params(pad=0.5)
        # x方向刻度
        plt.xticks([])
    plt.savefig(fig_name)
    plt.show()
 
boxplot(data, 'ml-vis5.pdf')
 

 

 使用四分位值筛选出箱线图中分布的异常值，并将这些数据视为噪声，其将被临界值取代，代码实现如下：

# 四分位处理异常值
num_features=data.select_dtypes(exclude=['object','bool']).columns.tolist()
 
for feature in num_features:
    if feature =='CHAS':
        continue
    
    Q1  = data[feature].quantile(q=0.25) # 下四分位
    Q3  = data[feature].quantile(q=0.75) # 上四分位
    
    IQR = Q3-Q1 
    top = Q3+1.5*IQR # 最大估计值
    bot = Q1-1.5*IQR # 最小估计值
    values=data[feature].values
    values[values > top] = top # 临界值取代噪声
    values[values < bot] = bot # 临界值取代噪声
    data[feature] = values.astype(data[feature].dtypes)
 
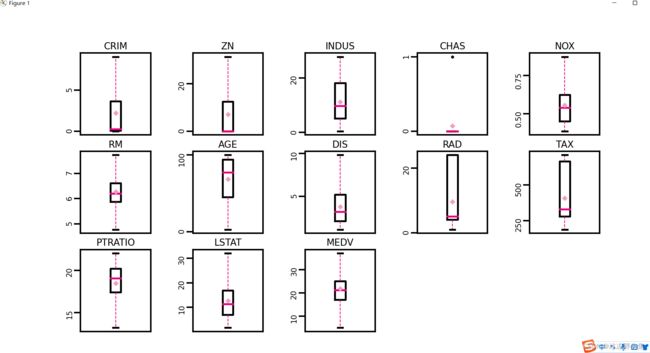
# 再次查看箱线图，异常值已被临界值替换（数据量较多或本身异常值较少时，箱线图展示会不容易体现出来）
boxplot(data, 'ml-vis6.pdf')
 

 运行结果

2.5.1.3 数据集划分 

import torch
torch.manual_seed(10)
 
# 划分训练集和测试集
def train_test_split(X, y, train_percent=0.8):
    n = len(X)
    shuffled_indices = torch.randperm(n)  # 返回一个数值在0到n-1、随机排列的1-D Tensor
    train_set_size = int(n * train_percent)
    train_indices = shuffled_indices[:train_set_size]
    test_indices = shuffled_indices[train_set_size:]
 
    X = X.values
    y = y.values
 
    X_train = X[train_indices]
    y_train = y[train_indices]
 
    X_test = X[test_indices]
    y_test = y[test_indices]
 
    return X_train, X_test, y_train, y_test
 
 
X = data.drop(['MEDV'], axis=1)
y = data['MEDV']
 
X_train, X_test, y_train, y_test = train_test_split(X, y)  # X_train每一行是个样本，shape[N,D]

 2.5.1.4 特征工程

#特征工程
import torch
X_train = torch.as_tensor(X_train,dtype=torch.float32)
X_test = torch.as_tensor(X_test,dtype=torch.float32)
y_train = torch.as_tensor(y_train,dtype=torch.float32)
y_test = torch.as_tensor(y_test,dtype=torch.float32)
X_min = torch.min(X_train,axis=0)[0]
X_max = torch.max(X_train,axis=0)[0]
X_train = (X_train-X_min)/(X_max-X_min)
X_test  = (X_test-X_min)/(X_max-X_min)
# 训练集构造
train_dataset=(X_train,y_train)
# 测试集构造
test_dataset=(X_test,y_test)

2.5.2 模型构建

#模型构建
from nndl.op import Linear
 
# 模型实例化
input_size = 12
model=Linear(input_size)

2.5.3 完善Runner类 

模型定义好后，围绕模型需要配置损失函数、优化器、评估、测试等信息，以及模型相关的一些其他信息（如模型存储路径等）。
在本章中使用的Runner类为V1版本。其中训练过程通过直接求解解析解的方式得到模型参数，没有模型优化及计算损失函数过程，模型训练结束后保存模型参数。
训练配置中定义:
训练环境，如GPU还是CPU，本案例不涉及；
优化器，本案例不涉及；
损失函数，本案例通过平方损失函数得到模型参数的解析解；
评估指标，本案例利用MSE评估模型效果。
在测试集上使用MSE对模型性能进行评估。
 

import torch.nn as nn
mse_loss = nn.MSELoss()

import torch
import os
from nndl.opitimizer import optimizer_lsm
class Runner(object):
    def __init__(self, model, optimizer, loss_fn, metric):
        # 优化器和损失函数为None,不再关注
 
        # 模型
        self.model = model
        # 评估指标
        self.metric = metric
        # 优化器
        self.optimizer = optimizer
 
    def train(self, dataset, reg_lambda, model_dir):
        X, y = dataset
        self.optimizer(self.model, X, y, reg_lambda)
 
        # 保存模型
        self.save_model(model_dir)
 
    def evaluate(self, dataset, **kwargs):
        X, y = dataset
 
        y_pred = self.model(X)
        result = self.metric(y_pred, y)
 
        return result
 
    def predict(self, X, **kwargs):
        return self.model(X)
 
    def save_model(self, model_dir):
        if not os.path.exists(model_dir):
            os.makedirs(model_dir)
 
        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        torch.save(model.params, params_saved_path)
 
    def load_model(self, model_dir):
        params_saved_path = os.path.join(model_dir, 'params.pdtensor')
        self.model.params = torch.load(params_saved_path)
 
 
optimizer = optimizer_lsm

 

#  optimizer_lsm
def optimizer_lsm(model, X, y, reg_lambda=0):
    N, D = X.shape
    # 对输入特征数据所有特征向量求平均
    x_bar_tran = torch.mean(X, axis=0).T
    # 求标签的均值,shape=[1]
    y_bar = torch.mean(y)
    # torch.subtract通过广播的方式实现矩阵减向量
    x_sub = torch.subtract(X, x_bar_tran)
    # 使用torch.all判断输入tensor是否全0
    if torch.all(x_sub == 0):
        model.params['b'] = y_bar
        model.params['w'] = torch.zeros(shape=[D])
        return model
    # torch.inverse求方阵的逆
    tmp = torch.inverse(torch.matmul(x_sub.T, x_sub) +
                         reg_lambda * torch.eye(num_rows=(D)))
 
    w = torch.matmul(torch.matmul(tmp, x_sub.T), (y - y_bar))
 
    b = y_bar - torch.matmul(x_bar_tran, w)
 
    model.params['b'] = b
    model.params['w'] = torch.squeeze(w, axis=-1)
 
    return model

2.5.4 模型训练 

在组装完成Runner之后，我们将开始进行模型训练、评估和测试。首先，我们先实例化Runner，然后开始进行装配训练环境，接下来就可以开始训练了

# 启动训练
runner.train(train_dataset,reg_lambda=0,model_dir=saved_dir)

打印出训练得到的权重： 

columns_list = data.columns.to_list()
weights = runner.model.params['w'].tolist()
b = runner.model.params['b'].item()
 
for i in range(len(weights)):
    print(columns_list[i],"weight:",weights[i])
 
print("b:",b)

 运行结果：

CRIM weight: -5.2611470222473145
ZN weight: 1.3627078533172607
INDUS weight: -0.02481861039996147
CHAS weight: 1.8001954555511475
NOX weight: -7.556739330291748
RM weight: 9.55705451965332
AGE weight: -1.3511563539505005
DIS weight: -9.967967987060547
RAD weight: 7.528563022613525
TAX weight: -5.082488059997559
PTRATIO weight: -6.9966607093811035
LSTAT weight: -13.183674812316895
b: 32.621612548828125
 

从输出结果看，CRIM、PTRATIO等的权重为负数，表示该镇的人均犯罪率与房价负相关，学生与教师比例越大，房价越低。RAD和CHAS等为正，表示到径向公路的可达性指数越高，房价越高；临近Charles River房价高。

3.5 模型测试 

加载训练好的模型参数，在测试集上得到模型的MSE指标。

# 加载模型权重
runner.load_model(saved_dir)

mse = runner.evaluate(test_dataset)
print('MSE:', mse.item())

运行结果：

MSE: 11.21076488494873
 

3.6 模型预测 

使用Runner中load_model函数加载保存好的模型，使用predict进行模型预测，代码实现如下：

runner.load_model(saved_dir)
pred = runner.predict(X_test[:1])
print("真实房价：",y_test[:1].item())
print("预测的房价：",pred.item())

 运行结果：

真实房价： 18.899999618530273
预测的房价： 21.529163360595703

问题
问题1：使用类实现机器学习模型的基本要素有什么优点？

我觉得使用类实现机器学习可以提高程序的执行效率，并且在程序出现问题时可以及时维护，并且成本低，相对更加灵活。

 问题2：算子op、优化器opitimizer放在单独的文件中，主程序在使用时调用该文件。这样做有什么优点？

简洁方便，更便于查找修改，便于整理归纳。

问题3：线性回归通常使用平方损失函数，能否使用交叉熵损失函数？为什么？

不能，交叉熵损失中有激活函数sigmoid，交叉熵损失函数主要用于离散情况，线性回归通常使用平方损失函数，适用于对预测值与真实值之间的误差求解。
 

---

总结

本次实验对我来说感觉比较难，可能是之前的基础打得不够牢，让我感觉自己的学的还不够，还得加把劲。通过这次试验也学到了很多东西，一些不熟悉的函数也通过网络查询了一番，跟着视频推到了一番，也算是对线性模型的建立有了个简单的了解。其中遇到的问题也很多，通过在B站上看博主的视频解决了一些，有的视频做的真不错，建议大家在学习中遇到困难也可以去看看，其中有一些暂时还是没有解决，但我相信在不懈努力下终究会解决他们。

最后附上本文参考链接

NNDL 实验2（下） - HBU_DAVID - 博客园 (cnblogs.com)https://www.cnblogs.com/hbuwyg/p/16617451.html3.3. 线性回归的简洁实现 — 动手学深度学习 2.0.0-beta1 documentation (d2l.ai)http://zh.d2l.ai/chapter_linear-networks/linear-regression-concise.html