Human-level control through deep reinforcement learning-2015 DQN论文研读

Human-level control through deep reinforcement learning-2015 DQN论文研读

DQN是强化学习的代表算法之一，它的原文是发表在Nature上的Human-level control through deep reinforcement learning，本篇博客主要从论文出发，介绍DQN的背景、算法要点、以及实验效果。

一、解决问题

本文主要解决了在高维输入下如何利用结合深度神经网络的强化学习打Atari游戏，从而让agent控制目标使得分最高。一个agent可以挑战多种游戏。

传统方法或者过去强化学习研究的局限：要手工提取特征；应用领域局限于完全可观测并且低维度的状态空间。

实验部分将之前文献[1]中的7个Atari游戏扩展到49个游戏中，其中29个效果超过人类水平。

二、强化学习基础

强化学习是与监督学习、非监督学习并列的第三种学习方法。它通过与环境的交互学习到最大化奖励的动作选择策略。

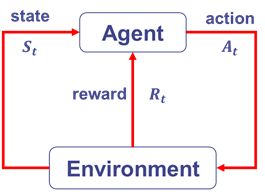
强化学习基本要素

1. 环境状态$S$：$t$ 时刻环境的状态 $S_t$ 是它的环境状态集中某一个状态。
2. Agent的动作$A$：$t$ 时刻个体采取的动作 $A_t$ 是它的动作集中某一个动作。
3. 环境的奖励$R$：$t$ 时刻Agent在状态 $S_t$ 采取的动作 $A_t$ 对应的奖励$R_{t+1}$会在$t+1$时刻得到。
4. Agent策略$\pi$：采取动作的依据，Agent会根据策略来选择动作。分为确定性策略$A=\pi (s)$与随机性策略$\pi (a|s)=P(A_t=a|A_t=s)$
5. 状态价值与动作价值：
   状态价值：Agent在策略$\pi$和状态$s$时，采取动作后的价值（value），一般用$v_{\pi }(s)$表示：
   $$v_{\pi }(s)=E_{\pi }[G_t|S_t=s]=E_{\pi }[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s]$$
   动作价值：Agent在策略$\pi$和状态$s$时，采取动作$a$后的价值，用$q_{\pi }(s,a)$表示：
   $$\begin{array}{rl}{q}_{\pi }(s,a)& =E_{\pi }[G_t|S_t=s,A_t=a]\\ & =E_{\pi }[\sum _{k=0}^{\infty }{\gamma }^k{R}_{t+k+1}|S_t=s,A_t=a]\end{array}$$
   其中$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+\cdots$，$\gamma$ 为衰减因子，在$[0,1]$之间，如果是0，表示贪婪法，价值只由当前延时奖励决定。如果是1，则所有的后续状态奖励和当前奖励一视同仁。大多数时候，我们会取一个0到1之间的数字，即当前延时奖励的权重比后续奖励的权重大。
6. 环境的状态转化模型，在状态 $s$ 下采取动作 $a$ ，转到下一个状态 $s’$ 的概率，表示为$P_{s{s}^{\prime }}^a$，一般情况下是潜在未知的。
7. 探索率：
   探索率（探索与利用之间的平衡）：在强化学习训练迭代的过程中，一般会选择使当前迭代价值最大的动作，但可能会导致一些较好但是没有试探过的动作被错过。因此在选择最优动作时，会有一定概率 $ϵ$ 选择其他动作。

三、算法要点

3.1 基本定义Agent和Emulator

Agent：每一步在游戏的动作集合中选择动作 $a_t$。
Emulator：执行动作获得奖励，模拟器提供当前游戏画面 $x_t$ ，游戏得分为奖励 $r_t$。

3.2 Q函数

对agent来说，目标是选择一个最大化未来累计奖励的动作。定义时刻t的未来折扣奖励为：
$$R_t=\sum _{t^{\prime }=t}^T{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots {\gamma }^T{r}_T$$
其中，$\gamma$ 为折扣因子，$T$ 为游戏结束的步数。
定义最优动作-价值函数$Q^{\ast }(s,a)$为：
$$\begin{array}{rl}{Q}^{\ast }(s,a)& =ma{x}_{\pi }E[r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+\cdots |s_t=s,a_t=a,\pi ]\\ & =E_{s^{\prime }}[r+\gamma ma{x}_{a^{\prime }}{Q}^{\ast }(s^{\prime },a^{\prime })|s,a]\end{array}$$
其中 $\pi$ 是序列到动作的映射或者是在动作上的分布。最优动作价值函数满足贝尔曼方程。

本文用了一个深度卷积神经网络来近似最优动作-价值函数（Q函数），即用$r+\gamma ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime };{\theta }^{-})$来近似目标Q函数的值，${\theta }^{-}$为神经网络参数。

3.3 优化算法

优化算法-RMSProp
损失函数：
$$\begin{array}{rl}{L}_i({\theta }_i)& =E_{s,a,r,s^{\prime }}[(y_i-Q(s,a;{\theta }_i){)}^2]\\ & =E_{s,a,r,s^{\prime }}[(r+\gamma ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime };{\theta }^{-})-Q(s,a;{\theta }_i){)}^2]\end{array}$$
梯度：
$${\nabla }_{{\theta }_i}{L}_i({\theta }_i)=E_{(}s,a,r,s^{\prime })[(r+\gamma ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime };{\theta }_i^{-})-Q(s,a;{\theta }_i)){\nabla }_{{\theta }_i}Q(s,a;{\theta }_i)]$$

RMSprop是自适应学习率优化方法，如果是普通SGD，学习率 $\eta$ 每次更新都不会变或者需要手动调节，这里的学习率随着t和i而改变，更新公式为：
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{(E[g^2{]}_t+ϵ)}}{g}_t$$
$$E[g^2{]}_t=0.9E[g^2{]}_{t-1}+0.1g_t^2$$
要想理解RMSprop，需要先了解Adagrad，它对低频的参数做较大的更新，对高频的做较小的更新，对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性。更新规则如下：
$${\theta }_{t+1,i}={\theta }_{t,i}-\frac{\eta }{\sqrt{(G_{t,ii}+ϵ)}}{g}_{t,i}$$
其中，$G_t$ 是个对角矩阵，$i,i$ 元素是对应参数 ${\theta }_i$ 从第1轮到第 $t$ 轮的梯度平方和。$ϵ$ 是平滑项，用于避免分母为0，一般取值 $1e-8$，g是t时刻 ${\theta }_i$ 的梯度
$$g_{t,i}={\nabla }_{\theta }J{\theta }_i$$
相比于Adagrad，Adagrad会累加之前所有的梯度平方，而RMSprop仅仅是计算对应的平均值（指数加权平均），因此可缓解Adagrad算法学习率下降较快的问题。

2.4 算法描述

• 与原DQN算法区别：加入了目标动作值函数Q（参数为 ${\theta }^{-}$）；
• 对于每一个状态s，ϵ贪心算法选择动作a，预处理函数ϕ(s)将4帧图片resize得状态向量84*84*4的向量；
• ϵ-greedy中的 $ϵ$ 在前100万帧样本从1编导0.1，之后为0.1不再变化；
• 每个k=
  4帧进行动作选择，中间跳过的帧保持执行上一个选择的动作。

2.5 算法细节

• 数据预处理
  $x_t$ 是游戏画面，原画面是210*160的128色图片，取当前帧与前一帧的最大值，从而避免闪烁，因为游戏中有的目标出现在奇数帧有的出现在偶数帧；需要将像素转为灰度值并且降采样到110*84，最后的输入是再通过裁剪得到游戏区域的84*84的图片，每次取最近的4帧图像来产生输入。所以输入是84*84*4的灰度图片。

• 卷积神经网络
  
  输入：84*84*4
  卷积1+relu：32个8*8的卷积核，stride=4
  卷积2+relu：64个4*4的卷积核，stride=2
  卷积3+relu：64个3*3的卷积核，stride=1
  全连接1：512个整流单元
  全连接2：有效action个单元的线性输出（游戏中动作范围为4-18）

  文中用了t-SNE降维方法对最后一个隐层的状态进行可视化，相近的点表示相似的状态。

• 经验回放机制
  经验池中存储了agent的每一步的experience，$e_t=(s_t,a_t,r_t,s_{t+1})$，随机在经验池抽样的优点：
  1).每步的经验都有可能在权重更新中被用到，保证了数据效率；
  2).打破了连续取样的相关性，降低了更新的方差；
  3).在线学习时，当前参数决定了下一个训练参数的样本，这样很容易参数陷入局部最小甚至不收敛。

  但是这个机制的缺点是，experience replay的容量有限（为N），存储的其实是最近的N条经验，数据没有优先程度。

• 目标网络定期更新
  降低了训练参数与目标的相关性。DQN（2013）里面，使用的目标Q值的计算方式为：
  $$y_j=\{\begin{array}{ll}{r}_j& \text{for terminal }{\varphi }_{j+1}\\ r_j+\gamma ma{x}_{a^{\prime }}Q({\varphi }_{j+1},a^{\prime };\theta )& \text{for non-terminal }{\varphi }_{j+1}\end{array}$$

  这里的目标Q值的计算要用到当前训练的Q网络参数来计算$Q({\varphi }_{j+1},a^{\prime };\theta )$，但是我们又希望通过$y_j$来更新Q网络参数，两者循环依赖，相关性太强，不利于算法的收敛。

  因此在本论文中使用的是同构网络，但是参数每隔一段时间更新一次。

• 其他训练细节

  • reward和errors控制为-1和1之间；
    在训练阶段，会调整奖励机制，正奖励设为1，负奖励设为-1，无奖励为0，因为不同的游戏奖励大小无法比较，这会影响到误差梯度的大小，从而不能使用相同的学习率；
  • ε-greedy策略保证有一定探索，ε从经过100万帧从1变为0.1，然后保持0.1不变；
  • mini-batch大小为32；
  • 每个k=4帧进行动作选择，中间跳过的帧保持执行上一个选择的动作（模拟器执行比选动作代价要小）；
  • 原始图片是310*160的彩色图片，预处理包括要1）取当前帧与前一帧的最大值，从而避免闪烁；2）resize到84*84的灰色图像；3）4帧选择一次。

四、实验

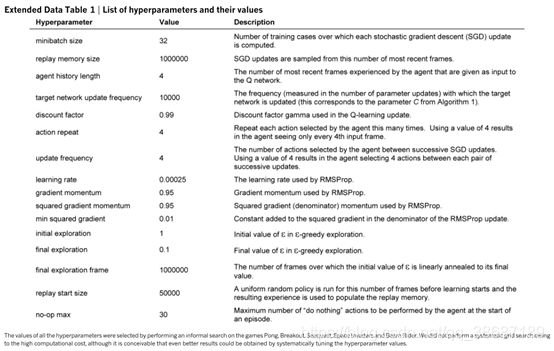
4.1 模型参数

4.2 对不同类型游戏的分析

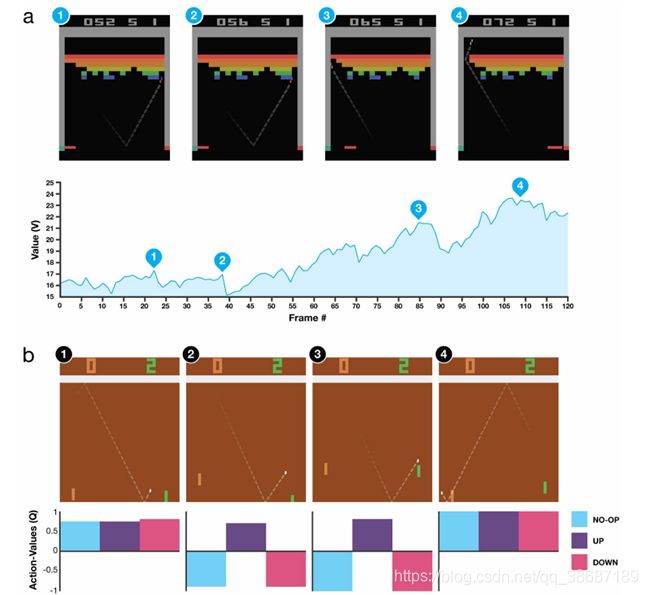
对不同类型的游戏，DQN表现出的结果也不太一样，通过实验发现，DQN比较擅长于需要相对长时间策略的游戏。比如打砖块(Breakout)，AI在游戏中学到了尽量在墙边打通一条通往顶部的路，这样球就会有很大的几率在上面自己碰撞消灭砖块而不需要玩家移动挡板。

参考文献

[1] Mnih, Volodymyr, et al. “Playing atari with deep reinforcement learning.” arXiv preprint arXiv:1312.5602 (2013).
[2]Mnih V, Kavukcuoglu K, Silver D, et al. Human-level control through deep reinforcement learning[J]. nature, 2015, 518(7540): 529-533.