神经网络学习笔记5——Swin-Transformer网络
系列文章目录
神经网络学习笔记1——ResNet残差网络、Batch Normalization理解与代码
神经网络学习笔记2——VGGNet神经网络结构与感受野理解与代码
参考博客1
参考博客2
文章目录
- 系列文章目录
- 前言
- 一、Patch Merging操作
- 二、W-MSA、SW-MSA与cyclic shift窗口设计
-
- 1、窗口自注意力W-MSA
- 2、移动窗口自注意力SW-MSA
- 3、窗口移动优化cyclic shift
- 三、Swin Transformer Blocks模块
- 四、整体模型理解
- 五、相对位置偏置Relative Position Bias参数
- 六、Swin transformer类别
前言
swin-transformer是什么?
- Swim Transformer是特为视觉领域设计的一种分层Transformer结构。Swin 的两大特性是滑动窗口和分层表示。滑动窗口在局部不重叠的窗口中计算自注意力,并允许跨窗口连接。分层结构允许模型适配不同尺度的图片,并且计算复杂度与图像大小呈线性关系,也因此被人成为披着transformer皮的CNN。
- Swin Transformer借鉴了CNN的分层结构,不仅能够做分类,还能够和CNN一样扩展到下游任务可以,用于计算机视觉任务的通用主干网络,可以用于图像分类、图像分割、目标检测等一系列视觉下游任务。
- 它以VIT作为起点,设计思想吸取了resnet的精华,从局部到全局,将transformer设计成逐步扩大感受野的工具,它的成功背后绝不是偶然,而是厚厚的积累与沉淀。
解决了什么问题?
- 与NLP领域不同,视觉领域同类的物体,在不同图像上/同一图像上的尺度会相差巨大,同一张多行人图中,行人会有大有小,有近有远,同一语义下的不同目标可能尺度差距变化会很大;
- 相较于文本,图像的尺寸过大,计算复杂度较高;
- 相比之前的ViT做了两个改进:引入CNN中常用的层次化构建方式构建层次化Transformer ;引入locality思想,对无重合的window区域内进行self-attention计算。
优点是什么?
- 提出了一种层级式网络结构,解决视觉图像的多尺度问题,提供各个尺度的维度信息;
- 提出Shifted Windows移动窗口,带来了更大的效率,移动操作让相邻窗口得到交互,极大降低了transformer的计算复杂度;
- 计算复杂度是线性增长而不是平方式增长,可以广泛应用到所有计算机视觉领域;
结论是什么?
- Transformer完全可以在各个领域取代CNN,被人称为CV领域的新方向,新时代
效果怎么样?
- 在ImageNet上并非SOTA,仅与EfficientNet的性能差不多
- swin-transformer的优点不是在于分类,在分类上的提升不是太多,而在检测、分割等下游任务中,有巨大的提升.
- 该论文是在2021年3月发表的,一经发表就已在多项视觉任务中霸榜。
一、Patch Merging操作

ViT用的是16×16的patch size,也就是16倍的下采样率,从低到高,这些token每个patch的尺寸并不会发生改变,通过全局自注意力操作来实现全局建模,可是面对多尺寸的目标的学习会较差,一单一尺寸处理为主。且面对大图片时序列长度还是过大,计算复杂度平方式递增。
在密集预测型任务如检测和分割或者说在落地项目中使用的图片,多尺度问题是很重要的问题,成熟的模型都会有专门的多尺度特征处理方法。
Swin transformer是在小窗口中进行自注意力(窗口概念在第二块),这些patch组成的小窗口和ViT的patch不同是相较独立的。比如4倍下采样中,将特征图划分成了多个不相交的小窗口区域,Multi-Head Self-Attention只在每个窗口patch内进行。
面对不相交的窗口如何传递信息,如何学习多尺度信息,它提出了patch merging,简单来说就是由小窗口patch合成大窗口patch增大感受野,再通过序号选取的方式去提取出深度特征图,模拟出一种类似池化的操作。
详细来说就是通过一个Patch Merging层进行下采样,如下图所示,比如想下采样两倍,先将四个小patch合成大patch,再通过小patch身上的序号1、2、3、4进行提取,提取的时候是每隔一个点选一个也就是选择同序号,同样序号位置上的 patch 就会被 merge。经过提取之后,原来的这个张量就变成了四个张量,在深度方向进行concat拼接,维度从h × w × c变为h/2 × w/2 × 4c,然后在通过一个LayerNorm层。因为要类比CNN模式,每次经过pooling后通道数只会翻倍,所以这里也只想让他翻2倍,而不是变成4倍,所以紧接着又再做了一次操作,就是在 c 的维度上用一个1x1的卷积(或者全连接层),把通道数降下来变成2c,最后就得到了h/2 × w/2 × 2c的输出。即通过Patch Merging层后,feature map的高和宽会减半,深度会翻倍。

二、W-MSA、SW-MSA与cyclic shift窗口设计
1、窗口自注意力W-MSA
像ViT的全局自注意力的计算会导致平方倍的复杂度,同样当去做视觉里的下游任务,尤其是密集预测型的任务,或者说遇到非常大尺寸的图片时候,这种全局算自注意力的计算复杂度对比卷积就会有很大算力差别。
文章提出用窗口的方式去做自注意力,也就是Windows Multi-head Self-Attention(W-MSA),W-MSA模块是为了减少计算量。
如下图所示,左侧使用的是普通的Multi-head Self-Attention(MSA)模块,对于feature map中的每个像素(或称作token或patch)与Class序列在Self-Attention计算过程中需要和所有的像素去计算全局。
但在图右侧,将特征图拆分成一个个不重叠的window,使用W-MSA模块时,首先将feature map按照M×M(例子中的M=2)大小划分成一个个Windows,然后单独对每个Windows内部进行Self-Attention。
假设在Swin transformer中输入224×224×3的图片,那么一个patch的大小划分为4×4,那么就有56×56个patch,而每7个patch就组成一个窗口,也就是一个窗口有7×7个patch,一个224×224×3的图片会有8×8=64个窗口。

原论文中有给出下面两个公式,这里忽略了Softmax的计算复杂度:

- h代表feature map的高度
- w代表feature map的宽度
- C代表feature map的深度
- M代表每个窗口(Windows)的大小,patch为单位
对比公式(1)和公式(2),虽然这两个公式前面这两项是一样的,只有后面从 (hw) ^ 2变成了 M^2 * h * w,看起来好像差别不大,但其实如果仔细带入数字进去计算就会发现,计算复杂的差距是相当巨大的,因为这里的 hw 如果是56*56的话, M^2 其实只有49,所以是相差了几十甚至上百倍。
2、移动窗口自注意力SW-MSA
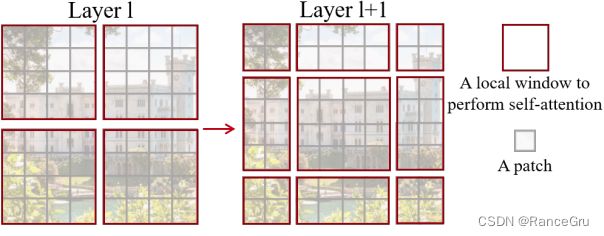
transformer初衷是理解上下文,是一种信息的传递交互,采用W-MSA模块时,只会在每个窗口内进行自注意力计算,所以窗口与窗口之间是无法进行信息传递的。为了解决这个问题,作者引入了Shifted Windows Multi-Head Self-Attention(SW-MSA)模块,即进行偏移的W-MSA。根据左右两幅图对比能够发现窗口发生了偏移(可以理解成窗口从左上角分别向右侧和下方各偏移了 M /2 个patch)。
在L1层使用的是W-MSA,L1+1层使用的是SW_MSA,在L1时每个窗口里的patch只能和同一个窗口里的patch相互学习,而到了L1+1层时,由于窗口的移动,导致一些patch进入新的窗口,这些带有上一层窗口信息的patch可以和别的带有上一层前窗口信息的patch相互学习。这就是跨窗连接cross window connection操作,使得窗口与窗口之间有着交互。再结合合并Patch Merging操作,在最后几层的时候,每个patch已经与特征图绝大部分的patch有过交流,也就是感受野已经很大了可以看见图片的绝大部分了。这些局部注意力信息最终会扩散到全局,变相达到全局注意力的效果。简单来说就L1+1层中心的4×4窗口学习融合的信息是L1层四个窗口的信息,因为中心的4×4窗口来源组成是L1层四个窗口的patch,L1层四个窗口的patch经过W-MSA时就已经学习到所在窗口的信息,带有自己窗口的信息。所以L1+1层中心的4×4窗口的学习就是L1层四个窗口的绝大部分相邻信息融合。
3、窗口移动优化cyclic shift
其实SW-MSA窗口的移动也存在问题,虽然实现让窗口里的patch可以和其他窗口的patch相互通信,交流到别的窗口的信息。可是移动的前后却带有一个问题,就比如移动前L1是四个窗口,每个窗口都是16个patch,移动后的L1+1是九个窗口,每个窗口大小不一,分别是4\8\16个patch。

有一种简单的做法,就是补零,比如把四个patch的窗口补多12个0,补成16个patch的窗口格式,这样4补12,8补8,补完后就得到9个窗口,再将9个窗口打成batch进行学习。虽然做法直白简单,但是一个batch里的窗口从4个提升到9个,实际上计算量提高了,复杂度也提高了。
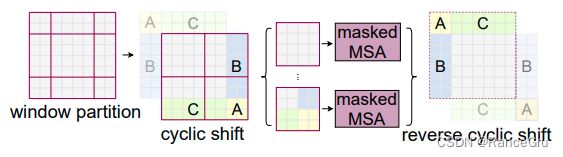
Swin transformer提出利用掩码做一次循环移位cyclic shift,具体的做法就是:
- 给L1+1的上方和左边的残缺窗口临时编号为A、B、C。
- 把A、B、C残缺窗口移动到L1+1的下方和右边,A是对角,B、C是对面。
- 将新建的特征图在划分为4个窗口,其中原中心16patch窗口不变,其他的残缺窗口拼接成新的16patch窗口。
这种操作即实现了不同窗口的patch交流,,又不会像补零操作那样窗口增加,计算复杂度提高。但是又产生新问题,就是原中心16patch窗口是不变的,里面的patch是本来就是像素意义上的邻居,是有关系的,可以两两相互做自注意力。可是对于另外3个拼接16patch窗口来说,它们是来自不同区域的特征图,如果它们之间做自注意力那么学习出来的特征可能是混乱的,也就是说它们之间不能当做一个纯粹的窗口去做自注意力。
如何处理拼接窗口,Swin transformer提出利用掩码masked操作

比如这里有一个已经进过移动拼接的14×14×3的特征图,0号窗口占7×7个patch,1号与3号是4×7个patch,2号与6号是3×7个patch,4号4×4,5号和7号是3×4,8号是3×3,一共就是14×14个patch(窗口从左上角分别向右侧和下方各偏移了 M /2 个patch)。
0号窗口是一个完整的窗口,可以直接使用自注意力,3号和6号是属于拼接窗口,它自身不可以直接做自注意力。
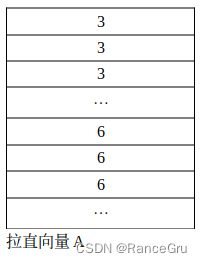
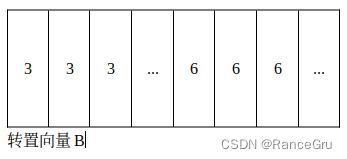
所以先执行前面的操作将3号方块和6号方块的patch提取出来,拉长为一个向量A,这个向量A中3号patch的值有4×7=28个,6号patch的值有3×7=21个。再通过向量A进行转置操作得到向量B。通过向量A、B的矩阵乘法进行自注意力计算,得到自注意力矩阵C,矩阵C中可以具体区分成四种类型,分别是:
- 向量A的所有3号patch值与向量B的所有3号patch值相乘,3×3
- 向量A的所有3号patch值与向量B的所有6号patch值相乘,3×6
- 向量A的所有6号patch值与向量B的所有3号patch值相乘,6×3
- 向量A的所有6号patch值与向量B的所有6号patch值相乘,6×6
其中3×3和6×6是符合自注意力理念的,3×6和6×3是拼接的混乱值,所以我们只需要3×3和6×6的数据,而3×6和6×3是需要masked掉的。
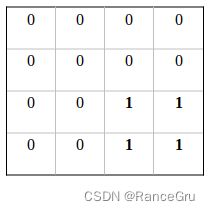
那么如何去处理3号方块+6号方块的窗口呢,Swin transformer提出一个巧妙的思路就是使用一个掩码模板矩阵D,让矩阵C与矩阵D相加,本来矩阵C里的那些数值是很小的值(大概是0点以下的值),3×3和6×6的数据加上0是不会变化的,而3×6和6×3的数据加上-100则会变成一个很大的负数,这是将这些值都进行softmax操作,那么那些负数就会归为0,剩下的也就是我们所需要的3×3和6×6数据。
讲完了3+6窗口那么继续看看1+2窗口,结合上面的思路,可以发现1+2窗口和3+6窗口是很不一样的,这个不一样产生于拉直向量A上。


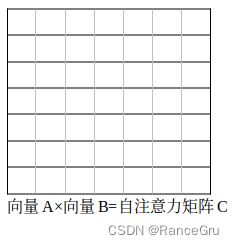
可以看见向量A里1号patch的值和2号patch的值是交错排序的,这也导致转置向量B以及自注意矩阵C的变化。
主要说说矩阵C的变化,它依然是分成4种类型(1×1,1×2,2×1,2×2),但不再是集中化和区域化了,而是一个横竖条纹围棋格式的矩阵,这种变化也导致了掩码模板矩阵D的设计,由于这种格式比较麻烦,我就没有专门一个个画出来,可以参考一下,Swin transformer提供的掩码模板。
至于4+5+7+8窗口,其实就是3+6和1+2窗口的合体,我就画了一个拉直向量A的图,具体可以自己去理解,需要结合3+6和1+2的规律。具体的掩码模板在上图有。

做完了多头自注意力后,需要把拼接的特征图还原回去,以保证它的相对位置不变,语义信息不变。如果不还原的话,那么循环轮到下一次Blocks模块时,学习的W-MSA是混乱的,学习SW-MSA时又将移动过的特征图继续拆分拼接,向右下角拼接,多轮下来学到的特征会越来越混乱,特征图也会处于不停打乱的状态。
三、Swin Transformer Blocks模块
Swin Transformer Blocks有两种结构,区别在于窗口多头自注意力的计算一个使用了W-MSA结构,一个使用了SW-MSA结构。而且这两个结构是成对使用的,先使用一个W-MSA结构再使用一个SW-MSA结构。所以堆叠Swin Transformer Block的次数都是偶数(在整体模型里Swin Transformer Blocks下的×2、×6就是因为成对使用的意思)。

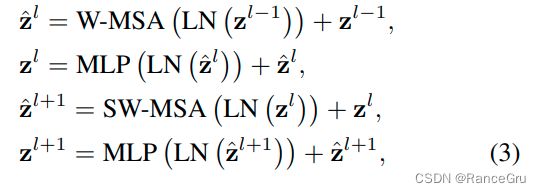
结合图片和公式进行前向模拟:
- 传入输入格式为[H/4n, W/4n, nC]的序列Z(l-1)。
- 传入LayerNorm层归一化后执行窗口自注意力W-MSA操作。
- W-MSA输出与Z(l-1)相加,输出为Z’l。
- 再传入LayerNorm层归一化后执行MLP操作,注意MLP Block输入的通道深度会×4,输出再÷4。
- MLP输出与Z’l相加,输出Zl。
- 传入输入格式为[H/4n, W/4n, nC]的序列Zl。
- 传入LayerNorm层归一化后执行移动窗口自注意力SW-MSA操作。
- SW-MSA输出与Zl相加,输出为Z’l+1。
- 再传入LayerNorm层归一化后执行MLP操作。
- MLP输出与Z’l+1相加,输出Zl+1。
四、整体模型理解
前向过程:
- 输入一张大小为H×W×3大小的图片Images。
- 执行patch partition,也就是将图片划分为H/4×W/4×48个patch(H/4×W/4×48=H×W×3),但不设置ClS token。
- 执行Linear Embedding,对每个像素的channel数据做线性变换,也就是说要把向量的维度变成一个预先设置好的值C(C值的设置与它的类型有关,就行resnet有18\34\50\101\152类型),这个C是一个超参数。即将图像的shape由 [H/4, W/4, 48]变成了 [H/4, W/4, C]。输入的数据[H/4, W/4]拉直变成H/4× W/4=HW/16序列长度,C变成每个token的向量维度。
- 因为[HW/16]个patch的序列长度比较长,比如说输入224×224×3的图片,那么patch就划分为56×56×48,那么序列长度就是3136patch,C为96,对比ViT的196patch来说太长了,所以就引入了给予窗口的自注意力计算。每个窗口一般设为7×7=49个patch的序列长度。
- [H/4, W/4, C]序列输入Stage1的Block,输出也是 [H/4, W/4, C],×2。
- 构建层级式transformer来提取多尺度信息,把Stage1的Block输出的[H/4, W/4, C]传入Patch Merging模块,进行类似池化下采样操作。它执行Patch Merging操作后输出的值是[H/8, W/8, 4C],模拟卷积模型的通道深度翻倍效果,进行1×1卷积将4C降为2C。
- [H/8, W/8, 2C]序列输入Stage2的Block,输出也是[H/8, W/8, 2C],×2。
- 把Stage3的Block输出的[H/8, W/8, 2C]传入Patch Merging模块,执行Patch Merging操作后输出的值是[H/16, W/16, 8C],模拟卷积模型的通道深度翻倍效果,进行1×1卷积将8C降为4C。
- [H/16, W/16, 4C]序列输入Stage3的Block,输出也是[H/16, W/16, 4C],×6。
- 把Stage4的Block输出的[H/16, W/16, 4C]传入Patch Merging模块,执行Patch Merging操作后输出的值是[H/32, W/32, 16C],模拟卷积模型的通道深度翻倍效果,进行1×1卷积将16C降为8C。
- [H/32, W/32, 8C]序列输入Stage4的Block,输出也是[H/32, W/32, 8C],×2。
- 以上就是整体骨干网络, 如果是用于图片分类,为了和卷积神经网络保持一致,Swin Transformer这篇论文并没有像 ViT 一样使用 CLS token,而是接上一个Layer Norm层、全局池化层以及全连接层得到最终输出。(作者这个图里并没有画,因为 Swin Transformer的本意并不是只做分类,它还会去做检测和分割,所以说它只画了backbone的部分,没有去画最后的分类头或者检测头)
五、相对位置偏置Relative Position Bias参数
Swin transformer在做实验的时候,表示做SW-MSA会比只做W-MSA好,做相对位置rel. pos.会比做绝对位置abs. pos.和没有位置no pos.好。

回到论文公式,会发现它的自注意力公式之前我们讲的多了一个+B操作,这个B就是相对位置偏置。
借用并参考这位博主的理解与图
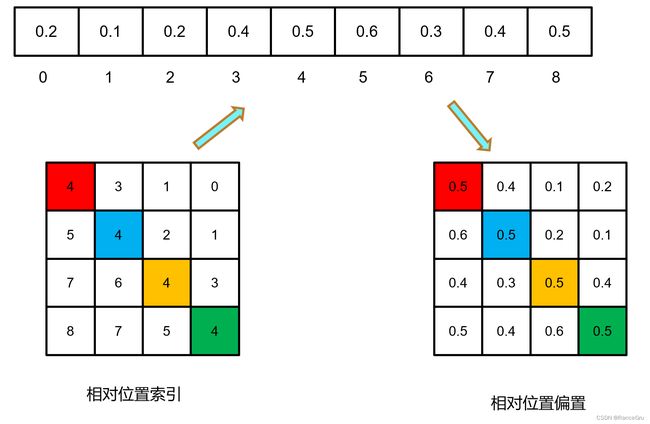
1、假设window的大小M×M是2×2patch,计算window内的自注意力时,先计算相对位置索引,这里的索引并不是偏置B,而是一个构成B的要素。

2、这里要区分出一个概念,就是绝对位置与相对位置,相对位置是可以结合参考系的方式理解,就是参考主体减去自身与参考客体计算而来。
3、不同的参考主体patch都可以计算出一种对应的相对位置索引,将每种计算出来的索引展平并拼接到一个矩阵A,A矩阵大小为(M×M)2。
4、我们可以观察A矩阵里的相对位置索引分布规律,就比如右边位置的位置概念,红色patch右边是蓝色,以红色为参考主体,蓝色的相对位置是[0,-1]。又比如黄色patch的右边是绿色,相对位置也会是[0,-1]。仔细观察后会发现上下左右,左上左下右上右下等位置概念是相同的索引的。
5、通过对行列做哈希变换,将2D的相对位置索引变为1D以精简计算,作者这里采用的哈希公式是(x+M-1)×(2M-1)+(y+M-1),其中x为行,y为列号,M为窗口大小。
6、将2D降为1D可以用相加或相乘等简单方法实现,但是会出现重复值,比如说红色patch右方是[0,-1],下方[-1,0],在2D时还是较明显的,但是用相加(-1)或相乘(0)时就会出现不同输入却输出相同的干扰,这时可以使用哈希算法来解决这个问题。
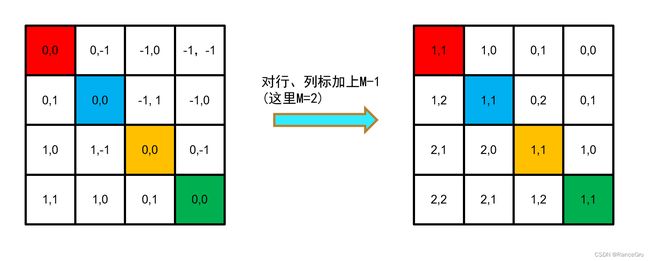



7、实现相对位置的特有值,相对位置索引总共有(2M-1)×(2M-1)种,那么就可以随机生成(2M-1)*(2M-1)个随机相对位置偏置(nn.Parameter可学参数),根据相对位置索引,去获取对应的相对位置偏置,也就是公式里面的B,进行多头自注意力的计算。
六、Swin transformer类别
- win. sz. 7x7表示使用的窗口(Windows)的大小
- dim表示feature map的channel深度(或者说token的向量长度)
- head表示多头注意力模块中head的个数
未完待续。。。