机器学习笔记 - 什么是支持向量回归(SVR)？

一、什么是支持向量回归

1、支持向量机

        在机器学习中，支持向量机是具有相关学习算法的监督学习模型，用于分析用于分类和回归分析的数据。在支持向量回归中，拟合数据所需的直线称为超平面。

         支持向量机算法的目标是在 n 维空间中找到一个对数据点进行明确分类的超平面。超平面两侧最接近超平面的数据点称为支持向量。这些影响超平面的位置和方向，从而有助于构建 SVM。

2、支持向量回归

        SVM 回归算法称为支持向量回归或SVR。支持向量回归是一种监督学习算法，用于预测离散值。支持向量回归使用与 SVM 相同的原理。SVR 背后的基本思想是找到最佳拟合线。在 SVR 中，最佳拟合线是点数最多的超平面。

          植根于统计学习或 Vapnik-Chervonenkis (VC) 理论，(SVM) 可以很好地概括尚未看到的数据。SVM概念可以推广到适用于回归问题。与分类一样，支持向量回归(SVR) 的特点是使用核、稀疏解和 VC 控制边距和支持向量的数量。

        尽管不如 SVM 流行，但 SVR 已被证明是实值函数估计的有效工具。作为一种监督学习方法，SVR 使用对称损失函数进行训练，这同样会惩罚高错误估计和低错误估计。使用 Vapnik 的-不敏感的方法，在估计函数周围对称地形成一个最小半径的柔性管，使得小于某个阈值的误差绝对值在估计值之上和之下都被忽略。以这种方式，管外的点会受到惩罚，但管内的点，无论是高于还是低于功能，都不​​会受到惩罚。

        SVR 的主要优点之一是其计算复杂度不依赖于输入空间的维度。此外，它具有出色的泛化能力，具有很高的预测精度。

3、支持向量回归优缺点

优点	缺点
对异常值具有鲁棒性。 决策模型可以轻松更新。 具有出色的泛化能力，具有很高的预测精度。 实现容易。	不适合大型数据集。 在每个数据点的特征数量超过训练数据样本数量的情况下，SVM 将表现不佳。 当数据集有更多噪声时，表现不佳，即目标类重叠。

4、原理简述

（1）线性回归

        在线性回归中，目标通常是为数据拟合一条回归线，以使偏差引起的误差最小。

        公式如下

        为了最小化这种偏差，首先，我们通过总结数据点和回归线之间的所有平方垂直差来制定优化问题。 然后，我们使用普通最小二乘法的技术来确定向量 W 和偏置项 b，从而使误差函数最小化。

         换句话说，简单线性回归的目标是最小化数据点与回归线的偏差。

 （2）支持向量

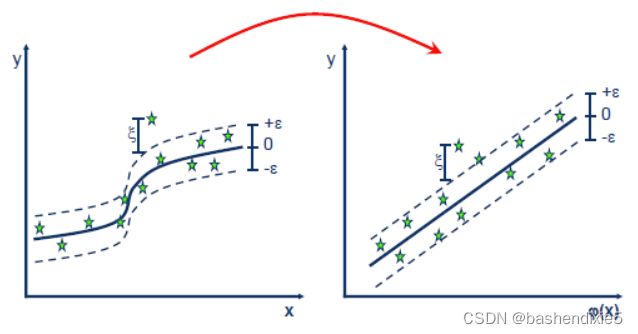
        与普通最小二乘法不同，SVR 模型在回归线周围设置了一个阈值ε，这样 ε 内的所有数据点都不会因其误差而受到惩罚。

        所以说SVM 对 SVR 的泛化是通过在函数周围引入一个ε不敏感区域来完成的，称为ε-管子。

一元线性SVR

         与普通最小二乘不同，SVR 模型设置了阈值误差容限ε围绕回归线，使得所有数据点在ε不会因为他们的错误而受到惩罚。

        支持向量机通过将二元分类问题表述为凸优化问题来解决二元分类问题（Vapnik 1998）。优化问题需要找到分离超平面的最大边距，同时正确分类尽可能多的训练点。SVM 用支持向量表示这个最优超平面。SVM 的稀疏解决方案和良好的泛化能力有助于适应回归问题。

        该管重新制定优化问题，以找到最接近连续值函数的管，同时平衡模型复杂性和预测误差。更具体地说，通过首先定义一个凸ε，将 SVR 表述为一个优化问题- 最小化不敏感损失函数并找到包含大多数训练实例的最扁平管。因此，多目标函数由损失函数和管的几何特性构成。然后，使用适当的数值优化算法求解具有唯一解的凸优化。超平面用支持向量表示，支持向量是位于管边界之外的训练样本。

        和 SVM 一样，SVR 中的支持向量是影响管子形状的最有影响力的实例，并且假设训练和测试数据是独立同分布(iid)，取自相同的固定但未知的概率分布函数在监督学习环境中。

（3）制定优化问题

         SVR将输入的数据的原始空间映射到更高维的特征空间，通常通过非线性高斯核函数实现。在特征空间中，问题变成了拟合数据的最优线性平面的构造。其中μ是偏差/基数，w是权重。因此，通过最小化向量范数w的平方来寻求最平滑的函数f(x)，每个训练数据的预测值的误差最多等于ε。为了允许异常值，预测误差大于ε的数据使用所谓的ε-敏感损失函数来惩罚。然后使用拉格朗日乘子将约束优化问题重新表述为对偶问题形式，对于每个约束，使用二次规划来确定，之后计算最佳权重的偏差，然后通过方程给出预测值。
 

        线性 SVR

        非线性SVR

         核函数将数据转换为更高维的特征空间，从而可以执行线性分离。

 

         内核函数

二、sklearn的SVR函数

        函数原型

sklearn.svm.SVR(*, kernel='rbf', degree=3, gamma='scale', coef0=0.0, tol=0.001, C=1.0, epsilon=0.1, shrinking=True, cache_size=200, verbose=False, max_iter=- 1)

        参数说明

参数	名称	数据	作用
kernel	核函数	1. string类型 2. {‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’} 3. 默认值为’rbf’	1. 用来选择映射到高维线性可分的核函数 2. linear: 线性核函数； 优点： 简单、运算效率高；缺点： 对线性不可分的数据集没有很好的效果 3. ploy: 多项式核函数； 优点： 可以拟合出复杂的分割超平面；缺点： 有三个参数，调参困难，且当n过大时，模型拟合时间会很长 ； 4. rbf: 径向基函数 通常定义为样本到数据中心之间径向距离（通常是欧氏距离）的单调函数（由于距离是径向同性的）； 相较于多项式核，具有参数少的优点 5. sigmoid：Logistic函数 也称为S型生长曲线，优点：平滑 6. precomputed：预训练好的核函数对应的Gram 矩阵 优点： 不用再次拟合核函数对应的Gram 矩阵，直接进行映射就可以了
degree	多项式核函数的维度	1. int类型，默认值为3	1. 只有在使用多项式核函数的时候才有用，使用其他核函数自动忽略此参数 2. 用来确定多项式核函数的维度，即n的值
gamma	‘rbf’, ‘poly’ 和‘sigmoid’ 核函数的系数	1. string类型，默认值为‘scale’ 2. {‘auto’, ‘scale’}	1. auto: gamma = 1 / n_features 2. scale: gamma = 1 / (n_features * X.var()) 3. 只作用于 rbf， poly，sigmoid 三个核函数
coef0	常数项	1. float类型，默认值为0	1. 只作用于poly 和 sigmoid 核函数 2. 作用相当于是对核函数映射的结果进行一个移位操作
tol	停止拟合容忍度	1. float类型，默认值为1e-3 即为0.001	1. 定义模型停止拟合的误差值
C	正则化系数	1. float类型，默认值为1.0	1. 正则化的强度与C的大小成反比，且必须为正。 2. 主要是用来防止模型过拟合 3. C值越大，对模型的惩罚越高，泛化能力越弱（过拟合） 4. 反之，C值越小，对模型的惩罚越低，泛化能力越强（欠拟合）
epsilon	希腊字母 ϵ	1. float类型，默认值：0.1	1. 用来定义模型对于错误分类的容忍度，即错误分类而不受到惩罚 2. ϵ 的值越大，模型允许错误分类的容忍度越高，反之，容忍度越小 3. 支持向量的个数对 ϵ \epsilonϵ 的大小敏感，即 ϵ \epsilonϵ 的值越大，支持向量的个数越少，反之，支持向量的个数越多 4. 也可以理解为ϵ \epsilonϵ 的值越小，模型越过拟合，反之，越大越欠拟合
shrinking	启用启发式收缩	1. bool类型，默认为True	1是否采用启发式收缩，当迭代次数过大时， 启用启发式收缩可以缩短训练时间，然而如果我们对停止迭代容忍度较高时（tol参数来反映），不用启发式收缩可能会更快一些
cache_size	核缓存大小	1. float类型，默认值为200（MB）	1. 指定模型在训练时，能占用的最大RAM空间（PS. 经过实验，当大小设置超过2000MB时，训练时长反而会增加，这应该是一个BUG），在2000MB以内，不超过其所需最大内存，则不会降低训练速度，也不会增加。 2. 所以训练多采用的数据集维度越高，条数越高，当所需内存超出了，我们可以通过调整cache_size 的大小来加快模型拟合
verbose	启用详细输出	1. bool类型，默认值：False	1. 该参数表示日志是否启用详细输出，会输出iter次数，nSV等参数的值 2. 如果启用，可能会导致无法进行多线程工作，降低拟合速率
max_iter	最大迭代次数	1. int类型，默认值: -1	1. 硬性设置最大迭代次数，不管模型是否拟合完成，即不关心误差值(tol参数) 2. 设置-1的话，意味着不限制迭代次数，即按照误差值来停止模型拟合

        属性说明

属性	名称	数据	作用
class_weight	各类权重	ndarray，一维数组，(n_classes, )	1用来获取模型对各个类别设置的权重，与参数中的class_weight相关
coef_	特征权重向量	1. ndarray，二维数组，(n_classes * (n_classes - 1) / 2, n_features)	1. 获取特征权重向量 2. 当核函数为linear时，才可以调用这一属性
dual_coef_	对偶系数	1. ndarray，二维数组，(n_classes -1, n_SV)	1. decision_funciton 中的支持向量的对偶系数 2. n_SV 为支持向量的个数 3. 所有 ovo 分类器的系数
fit_status_	拟合状态	1. int类型	1. 拟合成功0， 否则为1，进行告警
intercept_	决策函数常量	1. ndarray，一维数组， (n_classes * (n_classes - 1) / 2, )	1. decision_funciton 中的常量
n_features_in_	特征数量	1. int类型	1. 拟合过程中使用到的特征数量
feature_names_in_	特征名称	1. ndarray，一维数组，(n_features_in_,)	1. 获取拟合时特征的名称
n_support_	每类的支持向量数	1. ndarray，一维数组 ，(n_classes,), dtype=int32	1. 获取每种类别的支持向量数
shape_fit_	数组维数	1.元组，(n_dimensions_of_X,)	1.训练向量X的数组维数
support_	支持向量索引	1. ndarray，一维数组， (n_SV，)	1. 获取模型拟合后获得的所有支持向量的索引
support_vectors_	支持向量	1. ndarray，二维数组，(n_SV, n_features)	1. 获取所有的支持向量