【电子羊的奇妙冒险 】初试深度学习（4）

代码注释

随机数

出于我们的目的，我将创建一组具有根的此类多项式。实际上，我将首先创建根，然后创建多项式，如下所示：

import numpy as np

MIN_ROOT = -1
MAX_ROOT = 1

def make(n_samples, n_degree):
    global MIN_ROOT, MAX_ROOT
    y = np.random.uniform(MIN_ROOT, MAX_ROOT, (n_samples, n_degree))
    y.sort(axis=1) #，排序，参数axis = 1表示列,而0表示行
    X = np.array([np.poly(_) for _ in y])
    #numpy.poly(seq)：给出多项式根的序列，此函数返回多项式的系数
    #array()创建数组
    return X, y
#y为根，X为多项式系数
# toy case
X, y = make(1, 2)
print(X)
print(y)

uniform() 方法将随机生成下一个实数，它在 [x, y] 范围内
参见https://www.runoob.com/python/func-number-uniform.html

以下是 uniform() 方法的语法:

import numpy as np

np.random.uniform(x, y, size)

注意：uniform()是不能直接访问的，需要导入 random 模块，然后通过 random 静态对象调用该方法。
参数：

x – 随机数的最小值，包含该值。
y – 随机数的最大值，包含该值。
size: 输出样本数目，为int或元组(tuple)类型，例如，size=(m,n,k), 则输出m * n*k个样本，缺省时输出1个 实数

返回值：

取值范围为如果 x ndarray类型，其形状和参数size中描述一致

划分数据集

# make and train test split
N_SAMPLES = 100000  #样例数为100000
DEGREE = 5 #数据集根为5，多项式系数数量为5+1
X_train, y_train = make(int(N_SAMPLES*0.8), DEGREE)
X_test, y_test = make(int(N_SAMPLES*0.2), DEGREE)
#训练集/测试集 二八分
print(X_train.shape, y_train.shape)
print(X_test.shape, y_test.shape)
#np.shape 读取数组长度

reshape

# some dimensionality handling below
# this is because keras expects 3d tensors (a seq of onehot encoded characters) 
# but we have 2d tensors; just a sequence of numbers.


def reshape(array):
    return np.expand_dims(array, -1)
    
    
print(reshape(X_test).shape)  # batchsize, timesteps, input_dim (or "vocab_size")
print(reshape(y_test).shape) 
#注释上写到了，因为keras需要3d，所以使用np.expand_dims()补充一个轴的数据

模型建立

from keras.models import Sequential
from keras.layers import LSTM, RepeatVector, Dense, TimeDistributed


hidden_size = 128 #隐含层中，隐含节点的个数，LSTM里每一块都是一个全连接的神经网络，那么hidden_size就是这个神经网络的每一层的节点数目
model = Sequential()

# ENCODER PART OF SEQ2SEQ
model.add(LSTM(hidden_size, input_shape=(DEGREE+1, 1)))
#input_shape就是指输入张量的shape

# DECODER PART OF SEQ2SEQ
model.add(RepeatVector(DEGREE))  # this determines the length of the output sequence
#RepeatVector（n）改变输入维数为n

model.add((LSTM(hidden_size, return_sequences=True)))
model.add(TimeDistributed(Dense(1)))

model.compile(loss='mean_absolute_error',
              optimizer='adam',
              metrics=['mae'])
              
'''
model.compile(optimizer = 优化器，

                        loss = 损失函数，模型模型预测的好坏，表现预测与实际数据的差距程度

                        metrics = ["准确率”])
'''

print(model.summary())

Sequential模型详见链接

https://blog.csdn.net/mogoweb/article/details/82152174

return_sequences: Boolean. 是否返回最后一个输出或是整个序列的输出，默认是False

TimeDistributed用法：

https://blog.csdn.net/u012193416/article/details/79477220

Using TensorFlow backend.


_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
lstm_1 (LSTM)                (None, 128)               66560     
_________________________________________________________________
repeat_vector_1 (RepeatVecto (None, 5, 128)            0         
_________________________________________________________________
lstm_2 (LSTM)                (None, 5, 128)            131584    
_________________________________________________________________
time_distributed_1 (TimeDist (None, 5, 1)              129       
=================================================================
Total params: 198,273
Trainable params: 198,273
Non-trainable params: 0
_________________________________________________________________
None

注释：

# Param = （输入数据维度+1）* 神经元个数

模型定义

BATCH_SIZE = 128
model.fit(reshape(X_train),
          reshape(y_train),
          batch_size=BATCH_SIZE,
          epochs=5, #迭代次数
          verbose=1, #verbose：日志显示
          validation_data=(reshape(X_test), 
                           reshape(y_test)))
'''
batch_size：表示单次传递给程序用以训练的参数个数。
比如我们的训练集有1000个数据。
这是如果我们设置batch_size=100，
那么程序首先会用数据集中的前100个参数，
即第1-100个数据来训练模型。
当训练完成后更新权重，再使用第101-200的个数据训练，
直至第十次使用完训练集中的1000个数据后停止

model.fit()⽅法⽤于执⾏训练过程。
model.fit( 训练集的输⼊特征，
                 训练集的标签，  
                 batch_size,  #每⼀个batch的⼤⼩
                 epochs,   #迭代次数
                 validation_data = (测试集的输⼊特征，测试集的标签），
                 validation_split = 从测试集中划分多少⽐例给训练集，
                 validation_freq = 测试的epoch间隔数）

model.fit 中的 verbose
verbose：日志显示
verbose = 0 为不在标准输出流输出日志信息
verbose = 1 为输出进度条记录
verbose = 2 为每个epoch输出一行记录
注意： 默认为 1

'''

预测数据

y_pred = model.predict(reshape(X_test))
y_pred = np.squeeze(y_pred)

'''
model.predict
输入测试数据,输出预测结果
(通常用在需要得到预测结果的时候)
#模型预测,输入测试集,输出预测结果
    y_pred = model.predict(X_test,batch_size = 1）
    
squeeze 函数：从数组的形状中删除单维度条目，即把shape中为1的维度去掉
用法：numpy.squeeze(a,axis = None)
 1）a表示输入的数组；
 2）axis用于指定需要删除的维度，但是指定的维度必须为单维度，否则将会报错；
 3）axis的取值可为None 或 int 或 tuple of ints, 可选。若axis为空，则删除所有单维度的条目；
 4）返回值：数组
 5) 不会修改原数组；

'''

现在有一个功能可以帮助我们比较，我们可以重用

import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline


def get_evals(polynomials, roots):
    evals = [
        [np.polyval(poly, r) for r in root_row]
        for (root_row, poly) in zip(roots, polynomials)
    ]
    evals = np.array(evals).ravel()
    return evals
    

def compare_to_random(y_pred, y_test, polynomials):
    y_random = np.random.uniform(MIN_ROOT, MAX_ROOT, y_test.shape)
    y_random.sort(axis=1)
    
    fig, axes = plt.subplots(1, 2, figsize=(12, 6)) #画图，figsize为图像尺寸
    ax = axes[0]
    ax.hist(np.abs((y_random-y_test).ravel()),   #ravel()方法将数组维度拉成一维数组
            alpha=.4, label='random guessing') 
     #ax.hist()绘制直方图
    ax.hist(np.abs((y_pred-y_test).ravel()), 
            color='r', alpha=.4, label='model predictions')
    ax.set(title='Histogram of absolute errors',
           ylabel='count', xlabel='absolute error')
    ax.legend(loc='best')

    ax = axes[1]
    random_evals = get_evals(polynomials, y_random)
    predicted_evals = get_evals(polynomials, y_pred)
    pd.Series(random_evals).plot.kde(ax=ax, label='random guessing kde')
    pd.Series(predicted_evals).plot.kde(ax=ax, color='r', label='model prediction kde')
    title = 'Kernel Density Estimate plot\n' \
            'for polynomial evaluation of (predicted) roots'
    ax.set(xlim=[-.5, .5], title=title)
    ax.legend(loc='best')
    
    fig.tight_layout()
compare_to_random(y_pred, y_test, X_test)
'''
#polyval计算多项式的函数值。返回在x处多项式的值，p为多项式系数，元素按多项式降幂排序
y=polyval(p,x)

ravel()方法将数组维度拉成一维数组
'''

关于AXES用法详见：

https://article.itxueyuan.com/vOQMg9

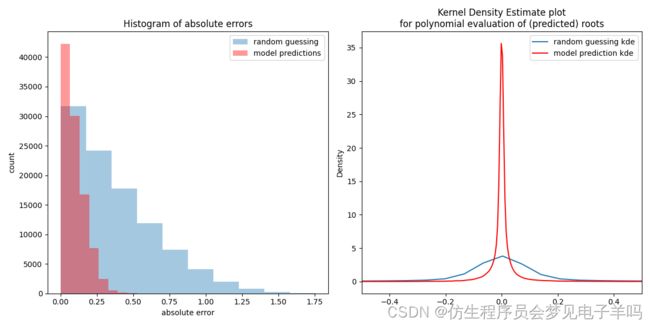
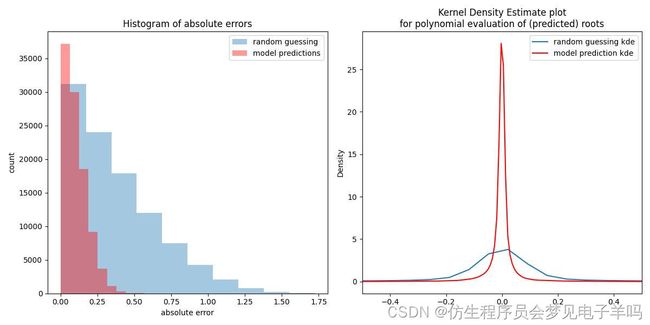
绘图

在左图中，请注意预测的根（红色条）如何更接近真实根（即红色条在 0.25 之后较小）。在右侧，请注意红色曲线在零附近有多紧。也就是说，在模型预测的根上，多项式评估的预期分布非常紧密地包含在零附近。至少这与e随机评估之间存在明显差异。

求解不同程度多项式

MAX_DEGREE = 15
MIN_DEGREE = 5 #大于4小于16次的多项式（5~15）
MAX_ROOT = 1
MIN_ROOT = -1
N_SAMPLES = 10000 * (MAX_DEGREE-MIN_DEGREE+1) #每一项都给出10000个示例，括号内为多项式各项总数，比如，三元一次方程左侧多项式为4项


def make(n_samples, max_degree, min_degree, min_root, max_root):
    samples_per_degree = n_samples // (max_degree-min_degree+1) #均分数据示例
    n_samples = samples_per_degree * (max_degree-min_degree+1) #得到相同数量示例之和
    X = np.zeros((n_samples, max_degree+1)) #返回来一个给定形状和类型的用0填充的数组
    # XXX: filling the truth labels with ZERO??? EOS character would be nice
    y = np.zeros((n_samples, max_degree, 2))
    for i, degree in enumerate(range(min_degree, max_degree+1)):
        y_tmp = np.random.uniform(min_root, max_root, (samples_per_degree, degree))
        y_tmp.sort(axis=1)
        X_tmp = np.array([np.poly(_) for _ in y_tmp])
        
        root_slice_y = np.s_[
            i*samples_per_degree:(i+1)*samples_per_degree,
            :degree,
            0]
        pad_slice_y = np.s_[
            i*samples_per_degree:(i+1)*samples_per_degree,
            degree:,
            1]
        this_slice_X = np.s_[
            i*samples_per_degree:(i+1)*samples_per_degree,
            -degree-1:]
        
        y[root_slice_y] = y_tmp 
        y[pad_slice_y] = 1
        X[this_slice_X] = X_tmp
    return X, y

def make_this():
    global MAX_DEGREE, MIN_DEGREE, MAX_ROOT, MIN_ROOT, N_SAMPLES
    return make(N_SAMPLES, MAX_DEGREE, MIN_DEGREE, MIN_ROOT, MAX_ROOT)


from sklearn.model_selection import train_test_split
X, y = make_this()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

'''
test_size：可以为浮点、整数或None，默认为None

①若为浮点时，表示测试集占总样本的百分比

②若为整数时，表示测试样本样本数

③若为None时，test size自动设置成0.25
'''


print('X shapes', X.shape, X_train.shape, X_test.shape)
print('y shapes', y.shape, y_train.shape, y_test.shape)
print('-'*80)
print('This is an example root sequence')
print(y[0])

改变模型

hidden_size = 128
model = Sequential()

model.add(LSTM(hidden_size, input_shape=(MAX_DEGREE+1, 1)))
model.add(RepeatVector(MAX_DEGREE))
model.add((LSTM(hidden_size, return_sequences=True)))
model.add(TimeDistributed(Dense(2)))

model.compile(loss='mean_absolute_error',
              optimizer='adam',
              metrics=['mae'])

print(model.summary())

训练模型

BATCH_SIZE = 12
model.fit(reshape(X_train), y_train,
          batch_size=BATCH_SIZE,
          epochs=10,
          verbose=1,
          validation_data=(reshape(X_test), y_test))

预测数据

y_pred = model.predict(reshape(X_test))
pad_or_not = y_pred[:, :, 1].ravel()
fig, ax = plt.subplots()
ax.set(title='histogram for predicting PAD',
       xlabel='predicted value',
       ylabel='count')
ax.hist(pad_or_not, bins=5);
#bins 指定条带bar 的总个数，个数越多，条形带越紧密
'''
bins ：数字或者序列（数组/列表等）。如果是数字，代表的是要分成多少组。如果是序
列，那么就会按照序列中指定的值进行分组。比如 [1,2,3,4] ，那么分组的时候会按照三个
区间分成3组，分别是 [1,2)/[2,3)/[3,4] 
'''

thr = 0.5


def how_many_roots(predicted):
    global thr
    return np.sum(predicted[:, 1] < thr)


true_root_count = np.array(list(map(how_many_roots, y_test)))
pred_root_count = np.array(list(map(how_many_roots, y_pred)))
from collections import Counter
for key, val in Counter(true_root_count - pred_root_count).items():
    print('off by {}: {} times'.format(key, val))

模型检验

index = np.where(true_root_count == pred_root_count)[0]
index = np.random.choice(index, 1000, replace=False)

predicted_evals, random_evals = [], []
random_roots_list = []
predicted_roots_list = []
true_roots_list = []
for i in index:
    predicted_roots = [row[0] for row in y_pred[i] if row[1] < thr]
    true_roots = [row[0] for row in y_test[i] if row[1] == 0]
    random_roots = np.random.uniform(MIN_ROOT, MAX_ROOT, len(predicted_roots))
    random_roots = sorted(random_roots)
    random_roots_list.extend(random_roots)
    predicted_roots_list.extend(predicted_roots)
    true_roots_list.extend(true_roots)
    for predicted_root, random_root in zip(predicted_roots, random_roots):
        predicted_evals.append(
            np.polyval(X_test[i], predicted_root))
        random_evals.append(
            np.polyval(X_test[i], random_root))
        
assert len(true_roots_list) == len(predicted_roots_list)
assert len(random_roots_list) == len(predicted_roots_list)
true_roots_list = np.array(true_roots_list)
random_roots_list = np.array(random_roots_list)
predicted_roots_list = np.array(predicted_roots_list)
fig, axes = plt.subplots(1, 2, figsize=(12, 6))
ax = axes[0]
ax.hist(np.abs(random_roots_list - true_roots_list),
        alpha=.4, label='random guessing') 
ax.hist(np.abs(predicted_roots_list - true_roots_list),
        color='r', alpha=.4, label='model predictions')
ax.set(title='Histogram of absolute errors',
       ylabel='count', xlabel='absolute error')
ax.legend(loc='best')

ax = axes[1]
pd.Series(random_evals).plot.kde(ax=ax, label='random guessing kde')
pd.Series(predicted_evals).plot.kde(ax=ax, color='r', label='model prediction kde')
title = 'Kernel Density Estimate plot\n' \
        'for polynomial evaluation of (predicted) roots'
ax.set(xlim=[-.5, .5], title=title)
ax.legend(loc='best')

fig.tight_layout()

高斯噪声的添加

首先，我们采用较小数据集：

N_SAMPLES = 100000
DEGREE = 5

对数据集加噪声

未加噪声（1）：

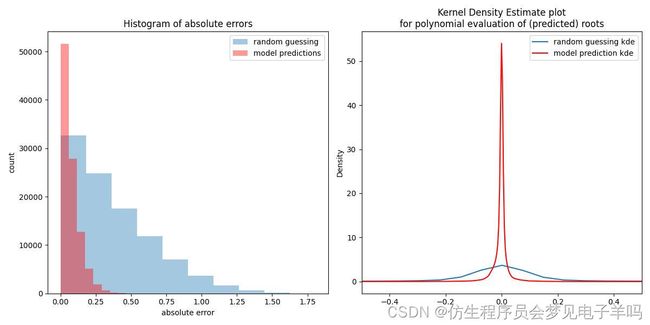
未加噪声（2）：

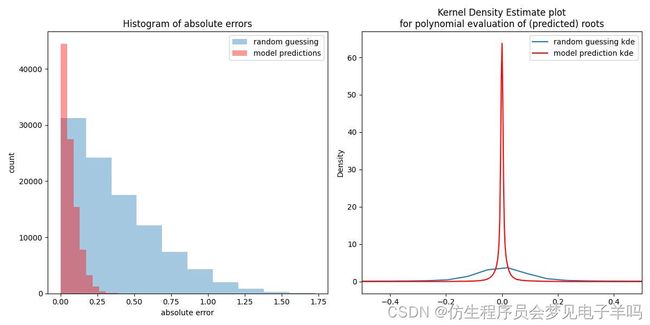
(sigma=0)-1

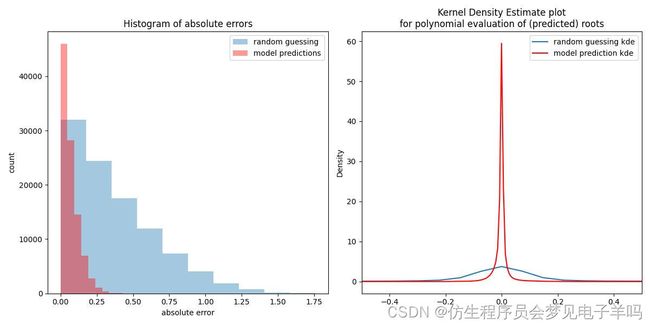
(sigma=0)-2:

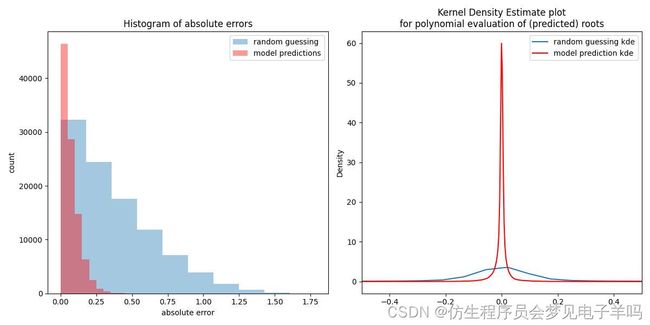
(sigma=0.05):

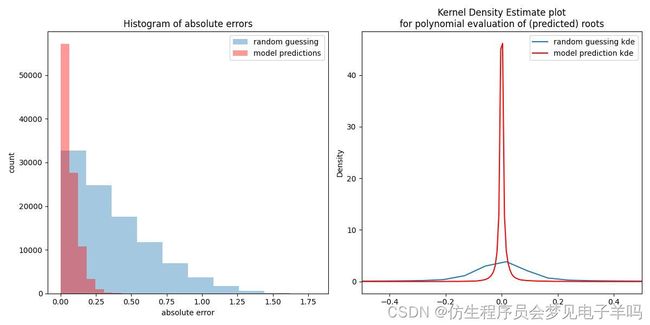
(sigma=0.5):

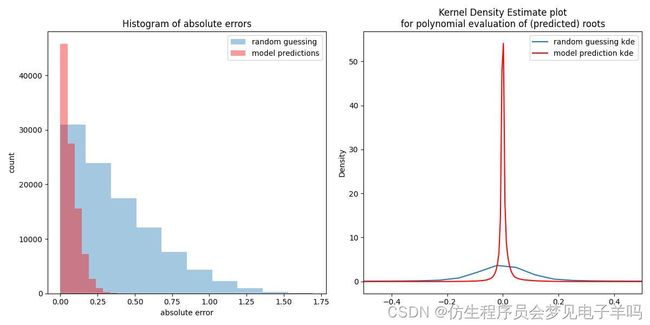
(sigma=1):

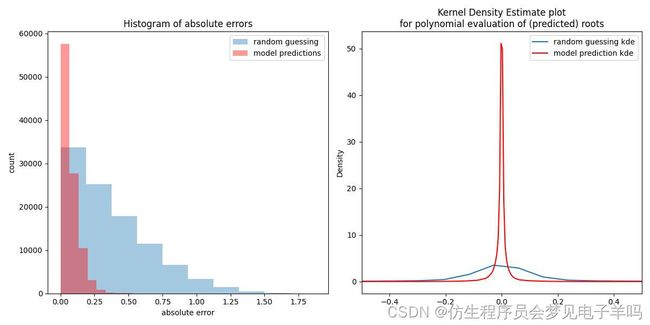
问题不大。

在函数中加噪声

def make(n_samples, n_degree):
    global MIN_ROOT, MAX_ROOT
    y = np.random.uniform(MIN_ROOT, MAX_ROOT, (n_samples, n_degree))
    y.sort(axis=1)
    X = np.array([np.poly(_) for _ in y])
    gauss_noisy(X, y)
    return X, y

(sigma=0)

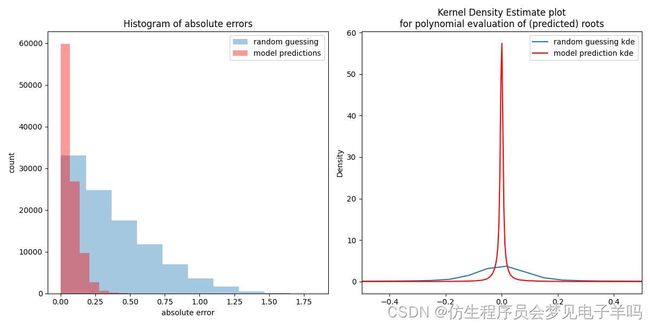（sigma=0.01）:

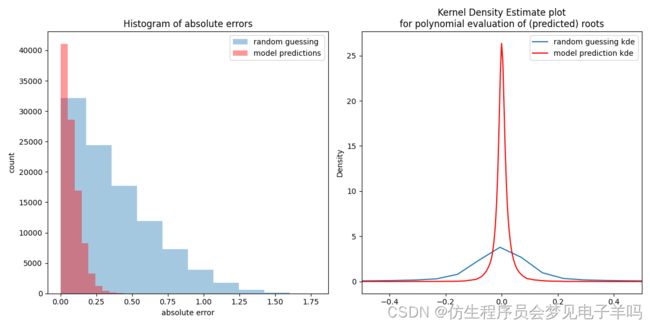
（sigma=0.05）:

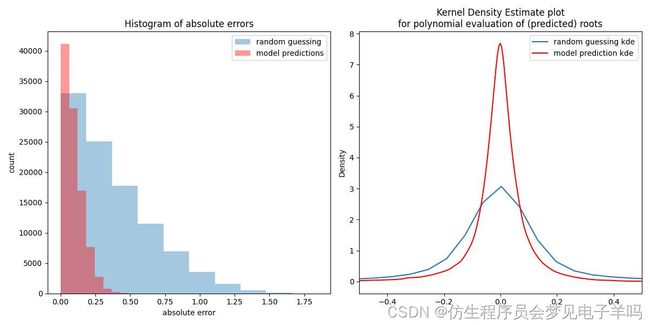
（sigma=0.1）:

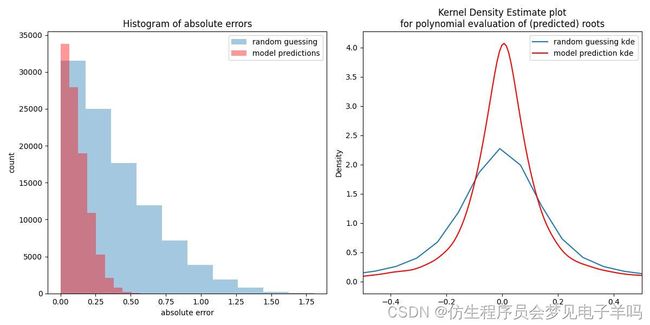
（sigma=0.1）:

在训练集中加噪声

gauss_noisy(X_train, y_train)

（sigma=0.05）:

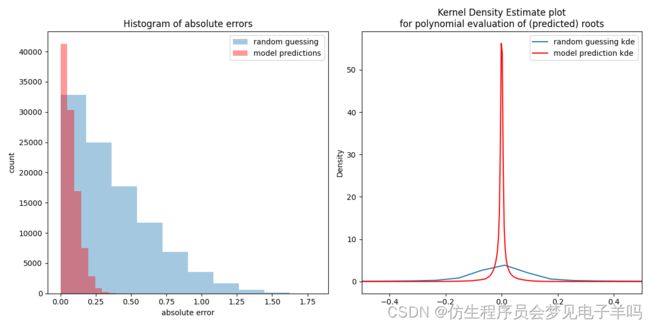
（sigma=0.05,epoch=10,l=4）:l为神经网络层数

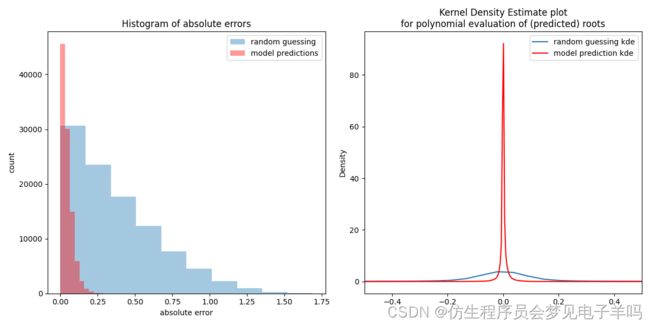
（sigma=0.1）:

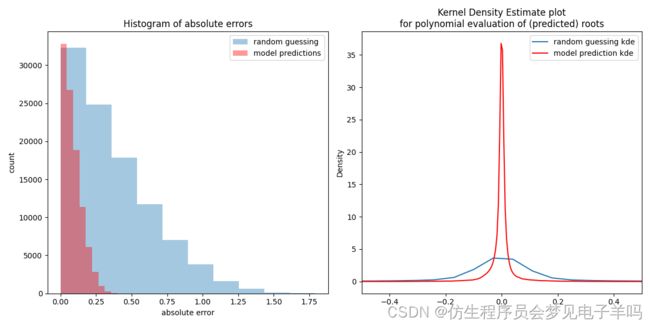
（sigma=0.1,epoch=5,l=4）:l为神经网络层数

（sigma=0.1,epoch=10,l=4）:l为神经网络层数

（sigma=0.5,epoch=5,l=2）:l为神经网络层数