图像分割（四）—— Is Space-Time Attention All You Need for Video Understanding?

Abstract

我们提出了一种无卷积的视频分类方法，专门建立在空间和时间上的自注意。我们的方法被命名为“时间转换器”，通过直接从一系列 frame-level patches中学习时空特征，将标准的变压器架构适应于视频。我们的实验研究比较了不同的自注意方案，并提出了“分散注意”，即时间注意和空间注意，可以在考虑的设计选择中获得最佳的视频分类精度。尽管采用了全新的设计，时间传感器在几个动作识别基准上取得了最先进的结果，包括 Kinetics-400和Kinetics-600的最佳报告精度。最后，与3D卷积网络相比，我们的模型训练速度更快，它可以实现显著更高的测试效率（精度略有下降），而且它也可以应用于更长的视频剪辑（超过一分钟）。

1. Introduction

视频理解与NLP的相似点

• Sequential 连续性：视频和句子都是连续的
• Contextual 具有上下文联系：句子中某个单词的意思通常需要通过将其与句子中的其他单词联系起来来理解；对于视频来说，为了消除歧义，片段中的行为也需要与视频的其余部分结合起来。

所以，NLP的自注意模型可能会对视频建模有效。因为其不仅可以捕捉跨时序的依赖关系，还可以通过对不同空间位置的特征进行两两比较，从而揭示每一帧中的上下文信息

因此，人们认为来自NLP的长期自注意模型对视频建模也非常有效。然而，在视频领域，二维或三维卷积仍然代表了不同视频任务的时空特征学习的核心操作，而自注意在应用于卷积层之上时也显示出了好处。

在这项工作中，我们提出了一个问题，即是否有可能通过用自注意完全取代卷积算子来建立一个无卷积性能的视频架构。我们认为，这样的设计有潜力克服视频分析的卷积模型的一些固有限制。

1. Inductive Bias 归纳偏置

   首先，虽然它们存在的强归纳偏差（例如，local connectivity and translation equivariance）无疑对小的训练集有益，但它们可能会过度限制模型在数据可用性充足且可以从例子中学习到的情况下的表达性。与cnn相比，变压器施加的限制性感应偏差更小。这扩大了它们可以表示的函数族，并使它们更适合现代大数据机制，在那里不太需要强归纳先验。

   增强数据操作的可能性

2. Short Range Temporal-spatial Imformation 捕捉的信息范围小

   其次，虽然卷积内核是专门为捕获短程时空信息而设计的，但它们不能建模扩展到接受域之外的依赖关系。虽然deep stacks of convolutions自然地扩展了接受域，但这些策略在通过聚合短程信息来捕获远程依赖方面受到固有的限制，相反，自注意机制可以通过直接比较所有时空位置的特征激活来捕获局部和全局的长期依赖关系，这远远超出了传统卷积滤波器的接受域。

3. 硬件计算

   尽管在GPU硬件加速方面取得了进步，但训练深度cnn仍然非常昂贵，特别是当应用于高分辨率和长视频时。最近在still-image领域的工作已经证明，与cnn相比，变压器享受更快的训练和推理，这使得在相同的计算预算下构建具有更大学习能力的模型成为可能。

基于这些观察结果，我们提出了一个完全建立在自注意力的基础上的视频架构。我们通过将自注意机制从图像空间扩展到时空三维体积，将图像模型“视觉变压器”(ViT)应用于视频。我们提出的模型，名为“TimeSformer”，将视频视为从单个帧中提取的patch序列。与ViT一样，每个patch都线性映射到嵌入并添加位置信息。这使得可以将生成的向量序列解释为可以输入给变压器编码器的标记嵌入，类似于从NLP中的单词计算出的标记特征。

标准变压器的自注意力的一个缺点是，它需要计算所有标记对的相似性度量。在我们的设置中，由于视频中存在大量的patch，这在计算上是昂贵的。为了解决这些挑战，我们提出了几种可伸缩的时空体积上的自注意设计，并在大规模的行动分类数据集上对它们进行了实证评估。在提出的方案中，我们发现最佳设计是由“分散注意”架构表示的，该架构在网络的每个块中分别应用时间注意和空间注意，与已建立的基于卷积的视频架构范式相比，时间形成器遵循了一个完全不同的设计。然而，它所达到的精度可与该领域的最先进水平相媲美，而且在某些情况下更优越。我们还表明，我们的模型可以用于跨越许多分钟的视频的远程建模。

2. Related Work

我们的方法受到了最近的工作的影响，这些工作使用自注意力进行图像分类，要么结合卷积算子，甚至作为它的完全替代，在前一类中，非局部网络(Wang et al. 2018b)采用了一种非局部均值，有效地推广了变压器的自注意力函数；Bello等人提出了一种二维自注意机制，该机制作为二维卷积的替代品具有竞争力，但当用于用自注意特征增强卷积特征时，会得到更强的结果。

我们的方法与利用自注意代替卷积的图像网络更密切相关，由于这些工作使用单个像素作为query，为了保持可管理的计算成本和较小的内存消耗，它们必须将自我注意的范围限制在局部邻域，或者在严重缩小的图像上使用全局自我注意。完整图像的可伸缩性替代策略包括稀疏键值采样(Child et al. 2019)或限制沿空间轴计算自注意力。在我们的实验中考虑的一些自注意力算子采用类似的稀疏和轴向计算，虽然推广到时空体积。然而，我们的方法的效率主要源于将视频分解为一系列帧级patch，然后将这些补丁的线性嵌入作为输入token输入到转换器。这一策略最近在视觉变压器(ViT)中引入(doso维特斯基等人，2020)显示，在图像分类方面提供了令人印象深刻的性能。在这项工作中，我们建立在ViT设计的基础上，并通过提出和经验比较几种可扩展的时空自我关注方案，将其扩展到视频。

3. The TimeSformer Model

Input clip. The TimeSformer takes as input a clip $X\in R^{H\times W\times 3\times F}$ consisting of $F$ RGB frames of size $H\times W$ sampled from the original video.

Decomposition into patches. 根据ViT，我们将每一帧分解为N个不重叠的patch，每个大小为$P\times P$，N个patch跨越整个帧，$N=HW/P^2$ . 接着将这些patch拉成一个向量 $x_{p,t}\in {\mathbb{R}}^{3p^2}$ 其中$p=1,...,N$ 表示空间位置，$t=1,...,F$ 表示帧上的索引。

Linear embedding. 我们通过一个可学习的矩阵$E\in {\mathbb{R}}^{D\times 3P^2}$ 将每个patch $x_{(p,t)}$ 线性映射到一个嵌入向量$z_{(p,t)}^{(0)}\in {\mathbb{R}}^D$ :
$${\mathbf{z}}_{(p,t)}^{(0)}=E{\mathbf{x}}_{(p,t)}+{\mathbf{e}}_{(p,t)}^{pos}\text{\hspace{1em}(1)}$$
嵌入向量${\mathbf{z}}_{(p,t)}^{(0)}$表示变压器的输入，发挥类似于NLP中输入文本变压器的嵌入词序列的作用。与最初的BERT变压器一样，我们在序列的第一个位置添加了一个特殊的可学习向量${\mathbf{z}}_{(0,0)}^{(0)}$，表示分类标记的嵌入。

Query-Key-Value computation. .我们的变压器由$L$ 个编码块组成。对于每个块$l$ ，每个patch的查询/键/值向量都是从之前的块编码表示${\mathbf{z}}_{(p,t)}^{(l-1)}$ 计算得来：
$$\begin{array}{l}{\mathbf{q}}_{(p,t)}^{(\ell ,a)}=W_Q^{(\ell ,a)}\mathrm{LN}\left({\mathbf{z}}_{(p,t)}^{(\ell -1)}\right)\in {\mathbb{R}}^{D_h}\\ {\mathbf{k}}_{(p,t)}^{(\ell ,a)}=W_K^{(\ell ,a)}\mathrm{LN}\left({\mathbf{z}}_{(p,t)}^{(\ell -1)}\right)\in {\mathbb{R}}^{D_h}\\ {\mathbf{v}}_{(p,t)}^{(\ell ,a)}=W_V^{(\ell ,a)}\mathrm{LN}\left({\mathbf{z}}_{(p,t)}^{(\ell -1)}\right)\in {\mathbb{R}}^{D_h}\end{array}$$
$a=1,...,A$ 是多个注意力头的索引，A表示注意力头的总数，每个注意头的潜在维数设置为$D_h=D/A$

Self-attention computation. 自注意权重通过点积计算，每个query patch (p,t)的自注意力权重计算公式为：
$${\mathbf{\alpha }}_{(p,t)}^{(\ell ,a)}=\mathrm{SM}\left(\frac{{\mathbf{q}}_{(p,t)}^{(\ell ,a{)}^{\top }}}{\sqrt{D_h}}\cdot \left[{\mathbf{k}}_{(0,0)}^{(\ell ,a)}{\left\{{\mathbf{k}}_{\left(p^{\prime },t^{\prime }\right)}^{(\ell ,a)}\right\}}_{\begin{array}{c}{p}^{\prime }=1,\dots ,N\\ t^{\prime }=1,\dots ,F\end{array}}\right]\right)\text{\hspace{1em}(5)}$$
其中，SM为softmax激活函数。当注意力只在一个维度上计算（例如，仅空间或仅时间）时，计算量会显著减少。例如，在空间注意的情况下，只使用N+1个query-key进行比较，即只使用与query来自同一帧的key：
$${\mathbf{\alpha }}_{(p,t)}^{(\ell ,a)space}=\mathrm{SM}\left(\frac{{\mathbf{q}}_{(p,t)}^{(\ell ,a{)}^{\top }}}{\sqrt{D_h}}\cdot \left[{\mathbf{k}}_{(0,0)}^{(\ell ,a)}{\left\{{\mathbf{k}}_{\left(p^{\prime },t^{\prime }\right)}^{(\ell ,a)}\right\}}_{\begin{array}{c}{p}^{\prime }=1,\dots ,N\end{array}}\right]\right)\text{\hspace{1em}(6)}$$
Encoding. ${\mathbf{z}}_{(p,t)}^{(l)}$ 是通过首先使用每个注意头的自注意系数计算值向量的加权和得到的：
$${\mathbf{s}}_{(p,t)}^{(\ell ,a)}={\alpha }_{(p,t),(0,0)}^{(\ell ,a)}{\mathbf{v}}_{(0,0)}^{(\ell ,a)}+\sum _{p^{\prime }=1}^N\sum _{t^{\prime }=1}^F{\alpha }_{(p,t),\left(p^{\prime },t^{\prime }\right)}^{(\ell ,a)}{\mathbf{v}}_{\left(p^{\prime },t^{\prime }\right)}^{(\ell ,a)}\text{\hspace{1em}(7)}$$
然后，来自所有头的向量的连接被投影并通过一个MLP，每次操作后使用残差连接：
$$\begin{array}{l}{\mathbf{z}}_{(p,t)}^{\prime (\ell )}=W_O\left[\begin{array}{c}{\mathbf{s}}_{(p,t)}^{(\ell ,1)}\\ ⋮\\ {\mathbf{s}}_{(p,t)}^{(\ell ,\mathcal{A})}\end{array}\right]+{\mathbf{z}}_{(p,t)}^{(\ell -1)}\\ {\mathbf{z}}_{(p,t)}^{(\ell )}=\mathrm{MLP}\left(\mathrm{LN}\left({\mathbf{z}}_{(p,t)}^{\prime (\ell )}\right)\right)+{\mathbf{z}}_{(p,t)}^{(\ell )}\end{array}$$
Classifification embedding. The fifinal clip embedding is

obtained from the fifinal block for the classifification token:
$$\mathbf{y}=\mathrm{LN}\left({\mathbf{z}}_{(0,0)}^{(L)}\right)\in {\mathbb{R}}^D\text{\hspace{1em}(10)}$$
在此表示之上，我们附加了一个1-hidden-layer MLP，用于预测最终的视频类。

Space-Time Self-Attention Models. 我们可以通过用每个帧内的空间注意力Eq(6) 替换Eq(5) 的时空注意来降低计算代价，然而，这样的模型忽略了捕获跨帧的时间依赖关系。正如我们的实验所示，与完全时空关注相比，这种方法导致分类精度下降，特别是在需要强时间建模的基准测试上。

我们提出了一种更有效的时空注意结构，称为“分割时空注意”(用T+S表示)，其中时间注意和空间注意分别被逐个应用。

图1 中该结构与空间和联合时空注意进行了比较

图2中给出了一个视频例子上不同注意模型的可视化

本文所研究的五种时空自注意方案的可视化研究，每个视频剪辑被视为一系列大小为16×16像素的帧级补丁。为了说明，我们用蓝色表示查询补丁，并用非蓝色表示其在每个方案下的自注意时空邻域。没有颜色的补丁不用于蓝色补丁的自注意计算。方案中的多种颜色表示分别应用于不同维度（例如（T+S）的空间和时间）或不同社区（例如（L+G））的注意。请注意，视频剪辑中的每个patch都计算了自注意力，也就是说，每个patch都作为一个Query. 我们还注意到，虽然注意力模式只显示了两个相邻的帧，但它以相同的方式扩展到剪辑的所有帧。

对于分散注意，在每个block $l$ 内，我们首先通过将每个patch (p,t)与其他帧中相同空间位置的所有patch进行比较来计算时间注意力：
$${\mathbf{\alpha }}_{(p,t)}^{(\ell ,a)\text{ time }}=\mathrm{SM}\left(\frac{{\mathbf{q}}_{(p,t)}^{(\ell ,a)}}{\sqrt{D_h}}\cdot \left[{\mathbf{k}}_{(0,0)}^{(\ell ,a)}{\left\{{\mathbf{k}}_{\left(p,t^{\prime }\right)}^{(\ell ,a)}\right\}}_{t^{\prime }=1,\dots ,F}\right]\right)\text{\hspace{1em}(11)}$$
利用时间注意应用Eq (8) 所得到的编码${\mathbf{z}}_{(p,t)}^{\prime (\ell )time}$ 被反馈给空间注意计算，而不是传递给MLP. 换句话说，新的键/查询/值向量从${\mathbf{z}}_{(p,t)}^{\prime (\ell )time}$ 得来，空间注意力通过等式(6) 计算得到。得到的向量${\mathbf{z}}_{(p,t)}^{\prime (\ell )time}$ 通过等式(9)的MLP去计算最终的编码${\mathbf{z}}_{(p,t)}^{(l)}$ 在block $l$ 的每个patch上，对于分散注意力的模型，我们学习不同的查询/键/值矩阵$\left\{W_{Q^{\text{time }}}^{(\ell ,a)},W_{K^{\text{time }}}^{(\ell ,a)},W_{V^{\text{time }}}^{(\ell ,a)}\right\}$和$\left\{W_{Q^{\text{time }}}^{(\ell ,a)},W_{K^{\text{time }}}^{(\ell ,a)},W_{V^{\text{time }}}^{(\ell ,a)}\right\}$ 在时间和空间维度上。值得注意的是，与等式5联合时空注意模型需要的每个patch (NF+1)比较相比，实验表明，这种时空分解不仅效率更高，而且提高了分类精度。

我们还实验了“稀疏局部全局”(L+G)和“轴向”(T+W+H)注意模型。它们的架构如图1所示，而图2显示了这些模型考虑注意的补丁。对于每个patch(p,t)，(L+G)首先考虑相邻的F×H/2×W/2斑块计算局部注意，然后沿时间维度和2个patch的步幅计算整个片段的稀疏全局注意。因此，它可以被视为使用局部-全局分解和稀疏模式的全时空注意近似，类似于(Childetal.，2019)中使用的。最后，“轴向”注意力将注意力计算分解为三个不同的步骤：随着时间的推移、宽度和高度。(Ho等人，2019年提出了分解注意力；Huang等人，2019；Wang等人，2020b)和我们的(T+W+H)为视频的情况添加了第三维度（时间），所有这些模型都是通过为每个注意步骤学习不同的查询/键/值矩阵来实现

4. Experiments

我们对四个流行的动作识别数据集进行了时间分析评估：Kinetics-400 , Kinetics-600, Something-Something-V2, Diving-48 。我们采用在ImageNet-1K或ImageNet-21K, 除非有不同说明，我们使用大小为8×224×224的剪辑，帧采样速率为1/32。补丁大小为16×16像素。在推理过程中，除非另有说明，我们在视频中间采样单个时间片段。我们从时间剪辑中使用3种空间作物（左上、中、右下），并通过对这3种作物的平均得分得到最终的预测。

4.1. Analysis of Self-Attention Schemes

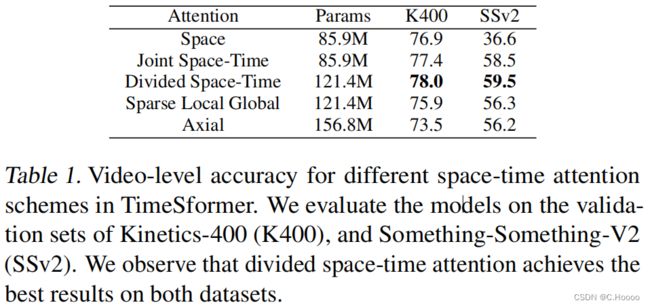
对于这第一组实验，我们从在ImageNet-21K上预训练的ViT开始。在表1中，我们给出了时间分析器对Kinetics-400 (K400)和Something-Something-V2 (SSv2)的五种时空注意方案的结果。首先，我们注意到具有仅空间注意(S)的时间s形成器在K400上表现良好。这是一个有趣的发现。事实上，之前的工作已经表明，在K400上，空间线索比时间信息更重要。在这里，我们证明了它是可能获得坚实的精度在K400没有任何时间建模。但是，仅空间注意在SSv2上表现很差。这强调了对后一个数据集进行时间建模的重要性。

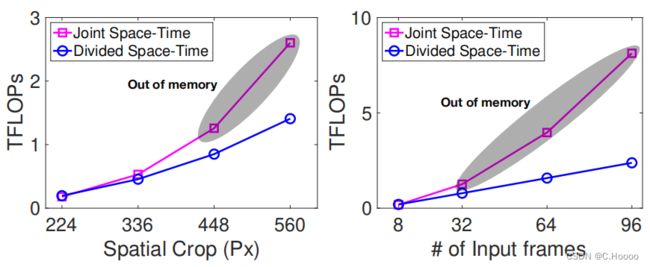
在图3中，我们还比较了在使用更高的空间分辨率（左）和更长的（右）视频时，联合时空与分割的时空注意力的计算成本。我们注意到，在这两种设置下，划分时空尺度的方案很优雅。相比之下，随着分辨率或视频长度时，联合时空注意方案的成本显著提高。在实践中，当空间帧分辨率达到448像素时，或当帧数增加到32像素时，联合时空注意就会导致GPU内存溢出，因此它实际上不适用于大帧或长视频。因此，尽管有更多的参数，但在更高空间分辨率或更长的视频时，分割时空注意比联合时空注意更有效。因此，在所有后续的实验中，我们都使用了一个由分割的时空自注意块构造的时间分析器。

4.2. Comparison to 3D CNNs

在本小节中，我们进行了一项实证研究，旨在理解TimeSformer与三维卷积架构的区别特性，这是近年来视频理解的突出方法。我们将比较重点放在两种3D CNN模型上：1)SlowFast，这是最先进的视频分类，和2)I3D，它已被证明受益于基于图像的预训练，类似于我们自己的模型。我们在表2中对这两个网络进行了定量比较，并强调了下面的关键观察结果。

Model Capacity.
从表2中，我们首先观察到，虽然TimeSformer具有较大的学习能力(参数数为121.4M)，但它的推理成本较低(TFLOPs为0.59)。相比之下，SlowFast 8x8 R50尽管只包含34.6M个参数，但仍具有更大的推理成本(1.97个TFLOPs)。类似地，I3D 8x8 R50也有更大的推理成本(1.11 TFLOPs)，尽管包含更少的参数(28.0M)。这表明，时间分布表更适合于涉及大规模学习的设置。相比之下，现代3Dcnn的计算成本很大，使得在进一步提高模型容量的同时保持效率。

Video Training Time
ImageNet预训练的一个显著优点是，它能够对视频数据进行非常有效的时间器训练，相反，即使在图像数据集上进行了预先训练，最先进的3Dcnn的训练成本也要昂贵得多。在表2中，我们比较了Timeformer在Kinetics-400的视频训练时间与SlowFast和I3D的视频训练时间。从在ImageNet-1K上预训练的ResNet50开始，SlowFast 8×8 R50需要3 840 Tesla V100 GPU hours才能在Kinetics-400上达到75.6%的精度。在类似的设置下，训练I3D需要1 440 Tesla V100 GPU hours，准确率为73.4%. 相比之下，同样在ImageNet-1K上进行预训练的时间发生器只需要416 Tesla V100 GPU hours就能达到更高的75.8%的准确率。此外，如果我们限制 SlowFast 在与Timeformer相似的计算预算下进行训练(即448 GPU hours)，其准确率降至70.0%. 类似地，使用类似的计算预算（即444个GPU hours）来训练I3D会导致准确率较低，为71.0%。这突出了一个事实，即一些最新的3Dcnn需要一个非常长的优化计划来实现良好的性能（即使使用ImageNet预训练），相比之下，Timformer 为实验室提供了一个更有效的替代方案。

The Importance of Pretraining.
由于有大量的参数，从头开始训练我们的模型是很困难的。因此，在对视频数据训练时间形成器之前，我们用从ImageNet学习的权值初始化它。相比之下，慢速度可以从头开始通过视频数据学习，尽管代价是非常高的训练成本（见表2）。我们还尝试直接训练Kinetics-400，不需要任何ImageNet预训练。通过使用更长的训练计划和更多的数据扩充，我们发现可以从头开始训练模型，尽管视频水平的精度要低得多，为64.8%。因此，基于这些结果，在所有后续研究中，我们继续使用ImageNet进行预训练（Deng et al.，2009）

在表3中，我们研究了ImageNet-1K与ImageNet-21K对K400和SSv2的预训练的好处。对于这些实验，我们使用三个版本的模型的： (1) Timesformer，这是模型的默认版本操作8×224×224视频剪辑，(2) Timesformer-HR，高空间分辨率变体操作$16\times 448\times 448$视频剪辑，最后(3) Timesformer-L，我们的模型运行在$96\times 224\times 224$ 视频剪辑与帧采样速度为1/4.

根据表3中的结果，我们观察到ImageNet- 21K预训练对K400有益，与ImageNet-1K预训练相比，它始终具有更高的准确性。另一方面，在SSv2上，我们观察到ImageNet-1K和ImageNet-21K的预训练导致了相似的精度。这是有意义的，因为SSv2需要复杂的时空推理，而K400更偏向于空间场景信息，因此，它从在更大的训练前数据集上学习到的特征中获益更多。

The Impact of Video-Data Scale.
为了理解视频数据规模对性能的影响，我们在K400和SSv2的不同子集上训练了时间s形成器：完整数据集的{25%, 50%, 75%, 100%}. 我们在图4中展示了这些结果，其中我们还将我们的方法与SlowFast R50 和I3DR50 进行了比较。由于我们没有使用在ImageNet-21K上进行预训练的ResNet，所以我们对所有3种架构都使用ImageNet-1K进行预训练。

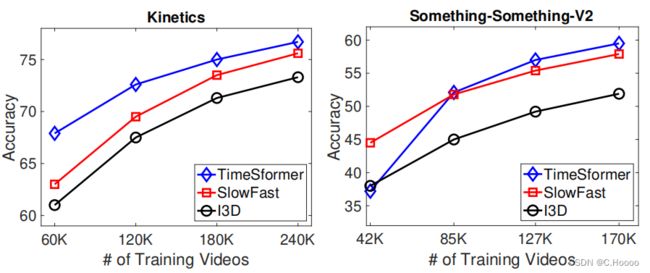
图4的结果显示，在K400上，时间器对所有训练子集的性能都优于其他模型。然而，我们在SSv2上观察到不同的趋势，只有在75%或100%的完整数据上训练时才是最强的模型。这可能是因为与K400相比，SSv2需要学习更复杂的时间模式，因此时间模式timefor需要更多的例子来有效地学习这些模式。