预测房价--基于python的线性回归模型

线性回归模型-预测房价

影响房价最大的因素就是房屋的面积和地段，本文章中针对房屋的面积作为主要影响因素，分析房屋面积对房价的影响

1.神经元模型
根据生物神经元的模型抽象出如图（1.1）所示的数学结构：神经元的输入向量$x=[x1,x2,x3,\dots \dots ,xn{]}^T$,经过函数映射：$f:x\to y$
，展开为标量形式：$f(x)=w1x1+w2x2+\cdots +b$，考虑到本文中对房价的影响因子，因为只讨论房屋的面积，所以构造的神经元模型标量表达式为：$f(x)=w_1\times x_1+b$

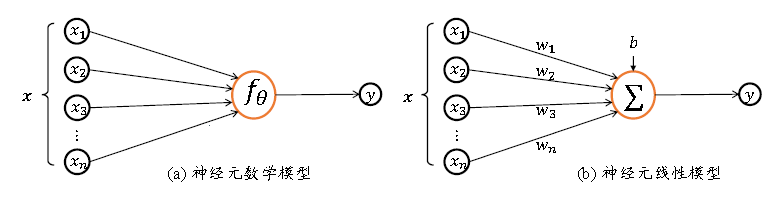
参数$\theta =w_1,w_2,\dots ,w_n,b$确定了神经元的形态，通过固定的θ参数即可确定此神经元的处理逻辑。（注：这里的$w$在《深度学习理论与应用》中叫做权重，是数组的形式；b称为偏置。有兴趣的小伙伴可以看看这本书）
通过上面的描述，我们建立预测模型，根据自变量与因变量，建立一元线性回归方程：$y=wx+b+\epsilon$（y表示每平米的房价，x表示面积，w,b为上文介绍的回归系数，ε作为观测误差：$\epsilon N(\mu ,{\sigma }^2）$均值为μ，方差为σ的二次方的正态分布，在实际的模型中$\epsilon$没有考虑进去）

2.损失函数
由于观测误差的存在，我们希望找到一组最贴合的直线去拟合若干的数据的点。我们使用均方误差作为损失函数。当我们拟合一条直线直线时，为了获得最拟合的直线，拟合直线的值与所有的数据做差，为了更好地表示，使用差平方的形式。故选择均方误差函数，表达式为：

然后我们需要搜索一组最优的参数$w^{\ast },b^{\ast }$使得损失函数的值最小；而寻找最优的w(权重)和b(偏置)，就要用到我们接下来要说的梯度下降法。

3.梯度下降法
梯度下降法在机器学习中应用十分广泛，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。梯度下降法可以用一个形象的例子来解释：假设一个人被困在山上，他需要从山上下来（找到山谷的最低点），但此时山上的浓雾很大，导致视线很低，因此下山的路径无法确定，必须利用自己周围的信息一步一步的找到下山的路径。这个时候，便可利用梯度下降法来帮助自己下山。怎么做呢？首先以她当前的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前的位置为基准，在寻找最陡峭的地方，再走一步，依次循环下去，直到走到山谷最低处。当应用到函数中，就是找到最优解（最优解也就是我们要求得的一元线性关系的权值和偏置项），梯度下降法又实现在模型的反向传播中。因为梯度的方向就是函数变化最快的方向。之前我们介绍均方误差作为损失函数的时候，我们希望损失函数达到最小，损失函数最小，也就是误差达到最小。此时我们就应用梯度下降法对均方误差求梯度。需要对$（w^{\ast },b^{\ast }）$不断地迭代更新，直到找到使均方误差最小。
数学理解为：函数的梯度是对各个自变量的偏导数组成的向量。函数对自变量x的偏导数记为$\partial z/\partial x$,函数对y的偏导数记为∂z/∂y,则梯度∇f为向量（∂z/∂x，∂z/∂y）。
函数在各处的梯度方向∇f总是指向函数值增大的方向。这里要最小化的是均方差误差函数L：也就是对这个方程式对w求偏导数，在对b求偏导数。这里迭代更新$w^{\prime }$和$b^{\prime }$的式子如下：
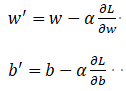
解释说明：（1）α在梯度下降法中称为学习率或者步长，意味着我们可以通过α来控制下山每一步走的距离，以保证不要步子跨的太大，错过最低点，同时也保证不要走得太慢，迟迟走不到最低点。
（2）梯度前加负号，就意味着朝梯度相反的方向走。梯度其实是函数在此点上升最快的方向。而我们需要朝着下降最快的方向走，所以添加负号。
在这里通过查阅资料直接给出∂L/∂w，∂L/∂b和的结果：

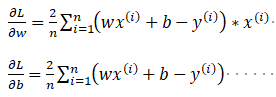
算法实现

# 计算赤峰面积和房价之间的关系

import numpy as np
import matplotlib.pyplot as plt

# 构建数据集
data = []
# (70-90,90-100,100-110,110-130)
for i in range(300):
    # 面积(训练集)
    area = np.random.uniform(60,100)  
    # 房价
    eps2 = np.random.uniform(60,62)
    # bias
    eps3 = np.random.uniform(200., 700.)
    # 总房价(标签)
    price = eps2 * area + eps3  # 随机生成一个线性方程，大小为（500，1）
    data.append([area, price])
data=np.array(data)  # 数据集创建完毕 2维数组 [面积,房价]

# 将参数分出来方便之后的使用
area = data[:,0]
price = data[:,1]
# 绘制原始数据
plt.title("Area-Price")  # 标题名
plt.scatter(area, price,s=10)  # 设置为散点图
plt.xlabel("area")  # x轴的标题
plt.ylabel("price")  # y轴的标题
plt.show()#绘制出来

# 创建一个loss值的list
loss_list = []

def mse(b, w, data):  # 根据当前的 w,b,参数计算均方差损失
    TotalError=0  # 记录总误差
    for i in range(0, len(data)):
        x = data[i, 0]
        y = data[i, 1]
        TotalError += (y - (w*x+b)) ** 2
    return TotalError / float(len(data))

def gradient_update(b, w, data, lr):
    b_gradient = 0
    w_gradient = 0
    size = float(len(data))
    for i in range(0, len(data)):
        x = data[i, 0]
        y = data[i, 1]
        # 计算梯度
        b_gradient += (2 / size) * ((w * x + b) - y)
        w_gradient += (2 / size) * x * ((w * x + b) - y)
    # 根据梯度更新权重和偏置
    b -= lr * b_gradient
    w -= lr * w_gradient
    return [b,w]

# 梯度下降法
def gradient_descent(data, b, w, lr, num_iterations):
    # 因为没有batch,所以num_iterations即为epoch
    for num in range(num_iterations):
        # 更新参数
        b,w = gradient_update(b, w, data, lr)
        # 计算损失值并添加到损失列表
        loss = mse(b, w, data)
        loss_list.append(loss)
        print('iteration:[%s] | loss:[%s] | w:[%s] | b:[%s]'%(num,loss,w,b))
    return [b,w]
    
 def main():
 	lr = 0.00001
    initial_b = np.random.randn(1)
    initial_w = np.random.randn(1)
    num_iterations = 100  # 因为没有batch,所以num_iterations即为epoch
    [b,w] = gradient_descent(data,initial_b,initial_w,lr,num_iterations)
    loss = mse(b,w,data)
    print('Final loss:[%s] | w:[%s] | b:[%s]'%(loss,w,b))
#损失函数
    plt.title("Loss Function")  # 标题名
    plt.plot(np.arange(0,100), loss_list)
    plt.xlabel('Interation')
    plt.ylabel('Loss Value')
    plt.show()
    # 绘制
    y2 = w * area + b
    print(w * 100 + b)
    plt.title("Fit the line graph")  # 标题名
    plt.scatter(area, price,label='Original Data',s=10)  # 设置为散点图
    plt.plot(area,y2,color='Red',label='Fitting Line',linewidth=2)
    plt.xlabel('m_j')
    plt.ylabel('j_g')
    plt.legend()
    plt.show()
main()

下面是实验结果，因为没有合适的真是的数据集，但是也是根据实际情况生成的数据集
原始数据集

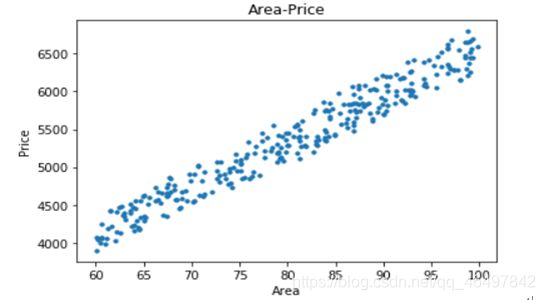
损失函数曲线，迭代20次左右，损失值就接近0了。

拟合的数据图像，也是根据原始数据预测房价的线性模型

（到这里就结束了，这是前段时间老师布置的任务，是一篇小论文，所以有大量的文字，如果有不懂的小伙伴，我这里有很详细的ppt，可以分享给你们。代码中预测了100平米的房价，得出的数据与真实值很接近，另外房价是每平米的房价，不是总房价，这个要注意一下！还有就是这是一元的线性回归，也就是自变量（影响因素是单一的），所以只要是一元的线性回归问题，都基本差不多；其实二元的也就是迭代更新那多了几步，方法同样是一样的。 内容是复制我的论文，可能错误有点多。继续加油吖！）
———————————————————————————————————————————————————
———————————————————————————————————————————————————
下面是基于pytorch的二元线性回归房价预测，不同于上面的一元线性回归，该模型使用了pytorch框架，真正的回归模型，比较遗憾的是影响房价的因素面积和楼层高度都是初始化的随机变量，而真实房价的标签也是初始化的随机值，如果小伙伴有自己的数据，直接在该代码的第一步准备数据，导入自己的数据就可以，代码写的很详细，另外还想说的是代码中的数据类型变换都是我自己一个一个搜的函数，可能存在冗余，但是又缺一不可（学了深度学习以后，自己写的每个模型都喜欢分为两个，一个训练文件，一个测试文件：训练文件负责把输入数据（多元自变量）加载进回归模型，找到输入与输出的关系（就是权值文件），测试文件负责把最优的模型参数（权值文件）在送入网络模型，实现预测），想了解更多请看：pytorch实现随机数据和真实文件数据的线性回归模型

• 1.训练文件

#计算赤峰面积和房价之间的关系
import torch as nn
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.autograd import Variable
#—————————————————————————————————————————————————————————————————————————————————————————
#步骤一：准备数据
#—————————————————————————————————————————————————————————————————————————————————————————
#房价影响因素一（面积）【50-100平米之间产生300个随机数】
area = torch.linspace(50,100,300)
#房价影响因素二（楼层）【1层到30层之间产生300个随机数】
tall = torch.linspace(1,30,300)
#bias = torch.rand(area.size())
#如果有真实的数据对应，真实的标签就不会是随机值，损失也就会更小
y = torch.linspace(300000,500000,300)
#最终的价格
#price = 3500*area + 2000*tall
#price = 3500*area + 1000*tall + torch.rand(area.size())
#为了能够自动求导，需要将面积和价格变成variable格式
x = Variable(area)
y = Variable(y)
input = []
input.append(area)
input.append(tall)
#input.append(bias)
input= torch.tensor([item.detach().numpy() for item in input])
#-->input为10行2列的tensor
#-->input为10行3列的tensor
input = input.t()
X = torch.from_numpy(np.array(input)).type(torch.FloatTensor)
#--> 行tensor变列tensor
Y = y.view(300,-1)
Y = torch.from_numpy(np.array(Y)).type(torch.FloatTensor)
#print("Y:",Y.shape)
#print(Y)
#—————————————————————————————————————————————————————————————————————————————————————————
#步骤二：构建模型
#—————————————————————————————————————————————————————————————————————————————————————————
#定义一个线性回归模型（单输入单输出、单输入多输出、多输入多输出）
#model = nn.Linear(2,1)
model=nn.Sequential(
                    nn.Linear(2, 6),
                    nn.ReLU(),
                    nn.Linear(6, 12),
                    nn.ReLU(),
                    nn.Linear(12, 1)
)
#—————————————————————————————————————————————————————————————————————————————————————————
#步骤三：损失函数和优化器
#—————————————————————————————————————————————————————————————————————————————————————————
#LOSS = nn.BCELoss()
LOSS = nn.L1Loss()
#optimizer=torch.optim.Adam(model.parameters(),lr=0.01)
#optimizer = torch.optim.SGD(model.parameters(),lr = 1e-3,momentum=0.8)
Cosine_lr = True
optimizer = torch.optim.Adam(model.parameters(), lr=0.1, weight_decay=5e-4)
#学习率余弦退火衰减法——用在模型中表现很优秀
if Cosine_lr:
    lr_scheduler = torch.optim.lr_scheduler.CosineAnnealingLR(optimizer, T_max=5, eta_min=1e-5)
else:
    lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, step_size=1, gamma=0.92)
#—————————————————————————————————————————————————————————————————————————————————————————
#步骤四：训练模型
#—————————————————————————————————————————————————————————————————————————————————————————
PATH = '.\\house-predict.pth'
num_epochs = 500
best_loss = 0
iter_loss = []
for epoch in range(num_epochs):
    #前向传播
    predict = model(X)
    #print("predict:",predict.shape)
    #计算损失
    loss = LOSS(predict,Y)
    # 目的是保存最优的参数
    if best_loss == 0:
        best_loss = loss
    if loss < best_loss and epoch > 100:
        best_loss = loss
        best_iter = epoch
        torch.save(model.state_dict(), PATH)
        print('保存模型')
    if (epoch % 20 == 0):
        print("-----------------------------------------------------------")
        print("第{}次迭代的loss是:{}".format(epoch, loss))
    iter_loss.append(loss.item())
    #优化损失函数
    #梯度清零
    optimizer.zero_grad()
    #误差反向传播
    loss.backward()
    #根据误差，优化函数
    optimizer.step()
print(f'{best_iter}:best loss:{best_loss}')

• 2.房价预测文件
  ~ ~ ~
  因为我的输入数据是随机的，真实的$target$标签也是随机的，所以训练下来损失依旧很大。所以在模型训练的时候，写入了保存最小损失的函数，也就是把最小损失的模型参数保存下来，这样测试的时候，加载的就是最优的参数。（model模型的架构不限于三层，自己可以随意尝试变换，一层，多层都可以，但最终的效果还是看层数和损失的变化），网盘链接包含处理真实文件数据，模型怎么导入数据的多元回归模型，以及随机生成数据的多元回归模型。
  训练预测文件，以及处理的文本数据可自行下载：
  链接：https://pan.baidu.com/s/1NZ5wKcRQ-b720cbNfKx0rw
  提取码：enzz