pytorch笔记：policy gradient

本文参考了 策略梯度PG（ Policy Gradient） 的pytorch代码实现示例 cart-pole游戏_李莹斌XJTU的博客-CSDN博客_策略梯度pytorch

在其基础上添加了注释和自己的一些理解

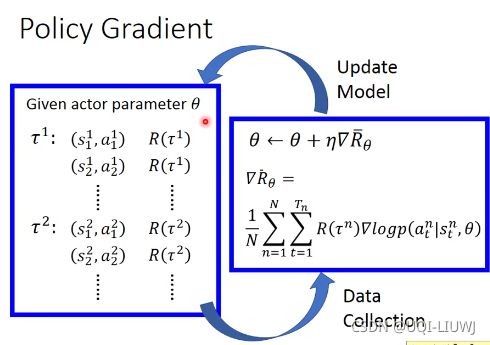
1 理论部分

强化学习笔记：Policy-based Approach_UQI-LIUWJ的博客-CSDN博客

我们使用其中的框架（在我们后面的实验中，我们认为每次N取1就对参数进行一次更新）

同时奖励R不是使用，而是使用折扣回报 

 2  代码部分

2.1 导入库 & 参数处理

import argparse
import numpy as np
import gym
from itertools import count
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.distributions import Categorical

parser = argparse.ArgumentParser(description='Pytorch REINFORCE example')
parser.add_argument('--gamma', type=float, default=0.99)
parser.add_argument('--seed',type=int, default=543)
parser.add_argument('--render',action='store_false')
parser.add_argument('--log-interval', type=int, default=10)
parser.add_argument('--episodes', type=int, default=10)
parser.add_argument('--steps_per_episode', type=int, default=10)


args = parser.parse_args()

python 笔记：argparse_UQI-LIUWJ的博客-CSDN博客

2.2 gym环境创建

python 笔记 ：Gym库 （官方文档笔记）_UQI-LIUWJ的博客-CSDN博客

env = gym.make('CartPole-v1')
#创建一个推车杆的gym环境
env.seed(args.seed)
#设置随机种子
torch.manual_seed(args.seed)
# 策略梯度算法方差很大，设置随机以保证复现性


print('observation space:',env.observation_space)
'''
Box([-4.8000002e+00 -3.4028235e+38 -4.1887903e-01 -3.4028235e+38],
    [4.8000002e+00 3.4028235e+38 4.1887903e-01 3.4028235e+38],
    (4,),
    float32)
'''

print('action space:',env.action_space)
#Discrete(2)

cartpole 的state是一个4维向量，分别是位置，速度，杆子的角度，加速度；

action是二维、离散，即向左/右推杆子

2.3 创建Policy类

输入某一时刻的状态（也就是一个四维向量），输出采取各个动作的概率（二维向量）

class Policy(nn.Module):
    ##  离散空间采用了 softmax policy 来参数化策略
    def __init__(self):
        super(Policy,self).__init__()
        self.fc1 = nn.Linear(4,128)
        #一开始是一个[1,4]维的Tensor，表示状态
        #先使用一个全连接层将维度升至128维

        self.dropout = nn.Dropout(p=0.6)

        self.fc2 = nn.Linear(128,2)
        # 两种动作 (取决于action_space,Discrete(2))
        # 再降维至每一个动作一个维度

        self.saved_log_probs = []
        #一个数组，记录每个时刻的log p(a|s)

        self.rewards = []
        #一个数组，记录每个时刻做完动作后的reward

    def forward(self, x):
        x = self.fc1(x)
        x = self.dropout(x)
        x = F.relu(x)
        action_scores = self.fc2(x)
        return F.softmax(action_scores,dim=1)
        #a[..][0],a[..][1],...a[..][n] 这些进行softmax
        #求得在状态x下各个action被执行的概率

policy = Policy()

optimizer = optim.Adam(policy.parameters(),lr=1e-2)

eps = np.finfo(np.float32).eps.item()  
# 非负的最小值，使得归一化时分母不为0

numpy 笔记：finfo_UQI-LIUWJ的博客-CSDN博客

2.4 选择动作

def select_action(state):
    ## 选择动作，这个动作不是根据Q值来选择，而是使用softmax生成的概率来选
    #  在policy gradient中，不需要epsilon-greedy，因为概率本身就具有随机性


    state = torch.from_numpy(state).float().unsqueeze(0)
    #print(state.shape)   
    #torch.size([1,4])
    #通过unsqueeze操作变成[1,4]维的向量
    
    probs = policy(state)
    #Policy的返回结果，在状态x下各个action被执行的概率
    
    m = Categorical(probs)      
    # 生成分布

    action = m.sample()           
    # 从分布中采样（根据各个action的概率）
    
    #print(m.log_prob(action))
    # m.log_prob(action)相当于probs.log()[0][action.item()].unsqueeze(0)
    #换句话说，就是选出来的这个action的概率，再加上log运算

    policy.saved_log_probs.append(m.log_prob(action))
    # 即 logP(a_t|s_t,θ)

    return action.item()         
    # 返回一个元素值

    '''
    所以每一次select_action做的事情是，选择一个合理的action,返回这个action;
    同时我们当前policy中添加在当前状态下选择这个action的概率的log结果
    '''

2.5 Policy 中参数的更新

def finish_episode(ep_reward):
    R = 0
    policy_loss = []
    returns = []

    for r in policy.rewards[::-1]:
        R = r + args.gamma * R
        #相当于是对时刻i而言 Σ(j ∈[i,t)) R^(j-i)，也就是之后考虑衰减的奖励和
        returns.insert(0,R)        
    # 将R插入到指定的位置0处（折扣奖励）

    returns = torch.tensor(returns)
    #所以returns的位数也和policy一样

    print(policy.saved_log_probs)
    '''
    一个类似于
    [tensor([-0.9295], grad_fn=),
     tensor([-0.5822], grad_fn=)]
     的list
    '''

    print(returns)
    #一个类似于tensor([8.6483, 7.7255])的tensor
    
    returns = (returns - returns.mean()) / (returns.std() + eps)
    # 归一化

    for log_prob, R in zip(policy.saved_log_probs,returns):
        #相当于 对 i ∈[0,len(returns)) 每次取saved_log_probs和returns相同下标的元素
        policy_loss.append(-log_prob * R)
        # 折扣奖励*logP(a|s)

    print(policy_loss)
    '''
    也是一个类似于
    [tensor([-0.9295], grad_fn=),
     tensor([-0.5822], grad_fn=)]
     的list
    '''

    
    policy_loss = torch.cat(policy_loss).sum()
    #torch.cat之后，变成tensor([-0.9295,-0.5822],grad_fn=)的形式
    #sum求和，也就是这个episode的总loss

    optimizer.zero_grad()
    policy_loss.backward()
    optimizer.step()
    #pytorch深度学习老三样

    del policy.rewards[:]          
    # 清空episode 数据
    del policy.saved_log_probs[:]

2.6 main函数

def main():
    running_reward = 10
    for i_episode in range(args.episodes):
        # 采集（训练）最多1000个序列
        
        state, ep_reward = env.reset(),0
        # ep_reward表示每个episode中的reward
        #state表示初始化这一个episode的环境

        state
        #array([-0.00352001,  0.01611176, -0.00538757, -0.00544052], dtype=float32)
        
        
        for t in range(1,args.steps_per_episode):
            #一个epsiode里面有几步

            action = select_action(state)
            #根据当前state的结果，按照概率选择下一步的action
            #同时我们当前policy中添加在当前状态下选择这个action的概率的log结果（后来的梯度上升中用）
            
            
            state, reward, done, _ = env.step(action)
            #四个返回的内容是state,reward,done(是否重置环境),info
            
            if args.render:
                env.render()
            #渲染环境，如果你是再服务器上跑的，只想出结果，不想看动态推杆过程的话，可以设置为False
                
            policy.rewards.append(reward)
            #选择这个action后的奖励，也添加到policy对应的数组中
            
            ep_reward += reward
            #这一个episode总的reward
            
            if done:
                break

        '''
        结束一个episode后，policy中会有两个等长的数组，一个是奖励，一个是概率的log结果
        它们两两对齐
        '''

        running_reward = 0.05 * ep_reward + (1-0.05) * running_reward
        #通过这种方式计算加权平均reward
        
        finish_episode(ep_reward)
        if i_episode % args.log_interval == 0:
            print('Episode {}\tLast reward: {:.2f}\tAverage reward: {:.2f}'.format(
                i_episode, ep_reward, running_reward))
        if running_reward > env.spec.reward_threshold:   # 大于游戏的最大阈值475时，退出游戏
            print("Solved! Running reward is now {} and "
                  "the last episode runs to {} time steps!".format(running_reward, t))
            break


if __name__ == '__main__':
    main()

3 和pytorch  深度学习的区别

可以看出来，主题框架和pytorch 深度学习（如pytorch笔记——简易回归问题_UQI-LIUWJ的博客-CSDN博客）是几乎一样的，不同的是，那里损失函数使用torch.nn中的一个直接调用的，这里相当于是自己设定，设定在一定程度上依赖于强化学习的奖励。

然后这里使用了折扣回报代替整体回报，同时我们每采一个episode就进行更新。我们也可以采样多个episode再进行更新，那样的话就是我一次性存储多个episode的奖励和概率，然后统一计算损失函数

梯度是随着P(a|s)传递的，反向传播也逆之更新模型各参数

4 结果

做了两组实验

一个的更新过程就是一个episode 全是这个episode的奖励 

可以看到他即使到了1000次也没有收敛

另一种更新的方法是折扣回报 

 可以看到它在进行700个episode的时候就结束了（平均reward大于475） 

 4 补充说明：离散动作 & 连续动作

• 要输出离散动作的话，可以加一层 softmax 层来确保说所有的输出是动作概率，而且所有的动作概率加和为 1。
• 要输出连续动作的话，一般可以在输出层这里加一层 tanh，把输出先限制到[-1,1]之间。拿到这个输出后，可以根据实际动作的范围再做缩放