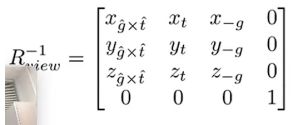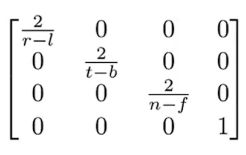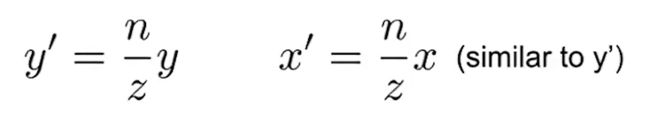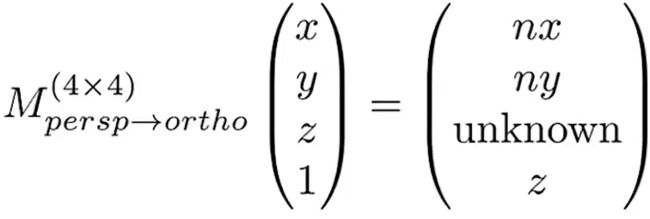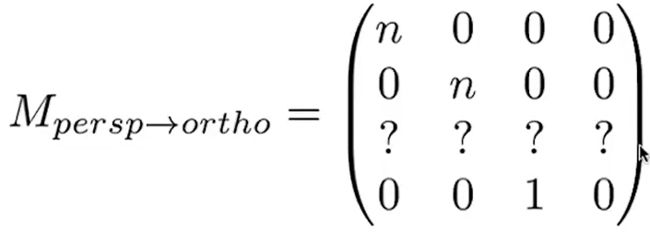Games101-课程4笔记

目录

 Viewing transformation(观测变换)

View/Camera transformation视图变换

Projection transformation 投影

Orthographic projection正交投影(工程制图)

Perspective Projection 透视投影(更偏向于人眼,近大远小)

这个内容能更好的梳理学到的内容

---

第四节课: Viewing transformation(观测变换)

--View/Camera transformation视图变换

视图变换主要是为了让摄像机回归到世界坐标的原点并且和拍摄物体一起进行变换,便于计算 . 视图变换的根据就是物体和相机的相对位置不变,那么,投影得到的图片也是不变的

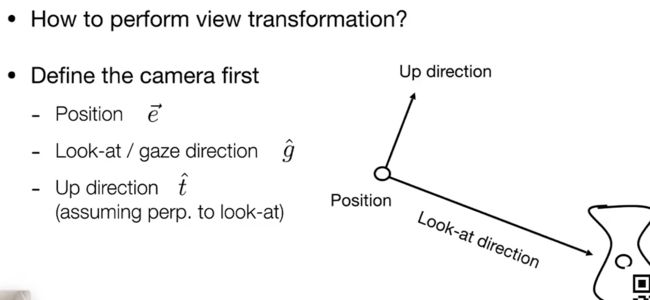
首先定义相机(位置 , 朝向)

 

当场景中的所有物体都一起移动时,相机所拍摄的图片是不变的.

约定俗成的相机位置为(0,0,0) , 朝向为 - z轴 , 还有它的向上方向

 

g表示目前相机看的方向, t表示目前相机的向上方向, g叉乘t就是目前相机的另一个轴方向.

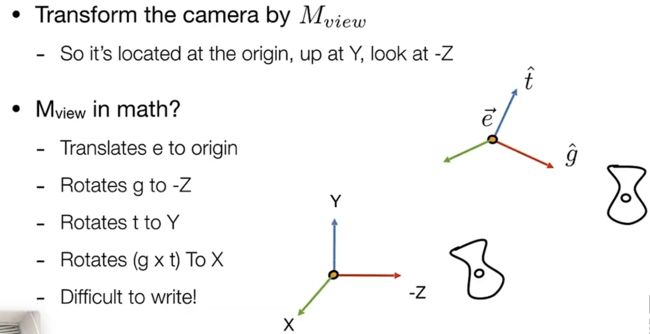
现在要将g旋转到-Z轴方向, t旋转到y轴,另一个轴旋转到x轴方向, 因为要将一个向量(x,y,z)旋转-Z轴(0,0-1), 会发现不好写.

所以要反过来写, 将 -Z轴(0,0,-1)旋转到目标相机向量(x,y,z), 旋转矩阵为

 

 然后通过定义:矩阵的逆==矩阵的转置,得到本来需要的旋转矩阵:

 

Projection transformation 投影

-Orthographic projection正交投影(工程制图)

使用的是右手系 , 所以为-Z方向 , z轴值近大于远.

这里假设将这个立方体投影到一个(-1~1 , -1~1 , -1~1)位置

先平移至原点, 平移矩阵 :

 然后缩放到(2 , 2)的大小, 缩放矩阵:

 

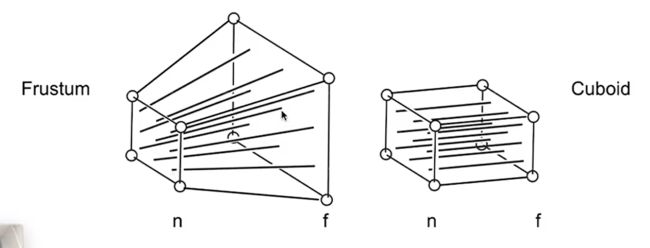
 t, b, l, r, n, f 各对应上、下、左、右、近、远平面

-Perspective Projection 透视投影(更偏向于人眼,近大远小)

如何将远处的平面挤压到近平面(左 -> 右)

 

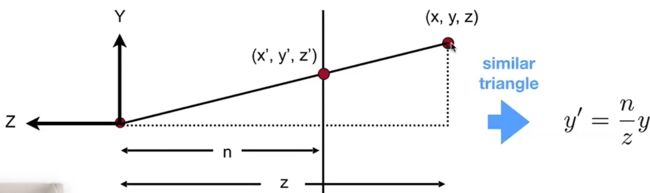
 利用相似三角形求出远点的y.

 所以, 根据点的z, 近面的n得出被挤压后的x,y

写出齐次方程 , z不知道 , 根据齐次方程中的性质('点'乘以任意值还是原来的'点')得到 :

推导出z的过程:

1.任意一点

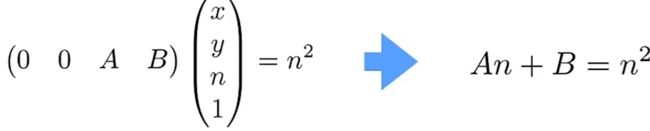
 2.得出对应的齐次方程 , 接下来求出剩余的(这一行数(0,0,A,B))

 3. n,f代表在 -z 轴上的距离 , 近面的点坐标不变&&远面的点坐标中的z是不变的.

 

4.根据近面的任意一点(利用其点坐标不变的性质)得出:

ps: 这里的n平方数,是为了后面方便计算, 才都乘以了n(点不变)

 

 单独拿第三行进行计算, 得出下图右边的等式

 

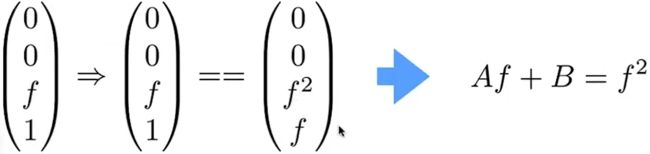
 5.根据远面的任意一点(利用其点坐标的z不变的性质)得出:

 6.根据上述两个方程,解出:

 

 7.

 

 8.得出透视投影矩阵 == 正交投影矩阵 乘以 透视变正交矩阵

 

这个内容能更好的梳理学到的内容.

 下面均取自哪个博主我也忘了(很久之前参考的), 这里标注: 下面这段话和图都不是原创.

---

在图形学的运行管线中，会经历模型变换（Model Transformation）到视图变换（View Transformation）最后再到投影变换（Projection Transformation）的过程。这里上节课讲述的仿射变换以及其他变换，都是针对世界坐标系下对于物体位置发生的改变，而在这一步结束之后，就会进行视图变换的操作。

简单理解，如果说模型变换是将所有需要渲染到屏幕上的模型放在一个场景内，那么视图变换就是确定相机位置，然后将原本世界空间坐标下的物体转换到视图空间，这样方便我们下一步的投影操作以及后续的操作。想象一下，一群人合照，大家在选择位置站好的过程就是模型变换，而摄像机选择角度和位置的过程就是视图变换，而最后按下快门选择拍照的过程，就称为投影变换。而这一整个流程在图形学管线中往往组合成为一个整体的变换矩阵，也就是MVP矩阵。