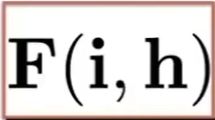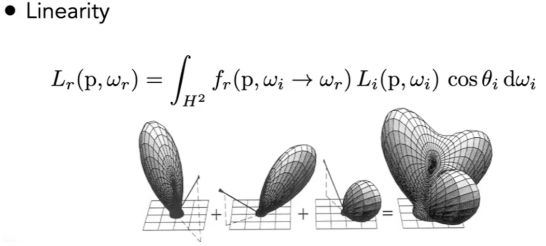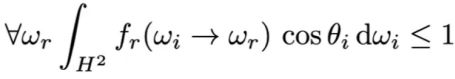Games101-课程17笔记

目录

什么是材质?

朗伯模型

ldeal reflective / refractive material(BSDF*)

反射公式

BTDF镜面折射

Snell’s Law(折射定律)

菲涅尔项

绝缘体(光密度为1.5)的菲尼尔项

导体的菲尼尔项

菲尼尔项公式

--近似值：schlick的近似值(得到广泛应用)

微表面模型

关键：微表面法线的分布

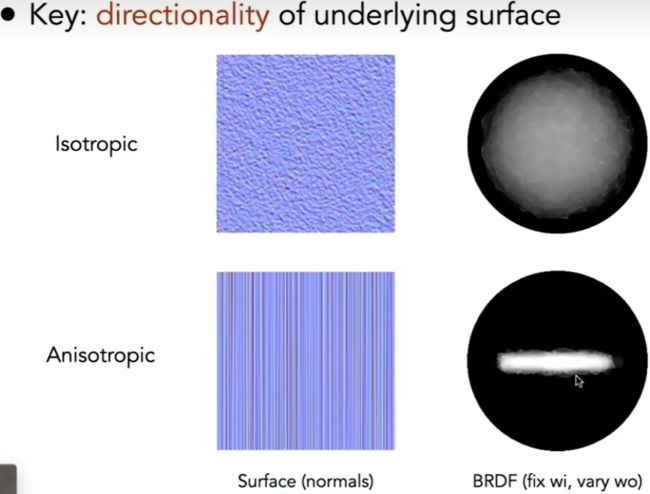
关键:   法线分布的方向性

总结: BRDF的性质

1.非负性

2.线性性质(可拆分)

3.互易性: 光传输路径可逆性

4.能量守恒

5.各向同性 vs. 各向异性

测量BRDFs (Measuring BRDFs)

---

第十七节课: 材质的外观

什么是材质?

 材质就是BRDF(双向反射分布函数)

                              均匀颜色漫反射BRDF                                纹理漫反射BRDF

 

lambertian material(朗伯模型)

最简单的 BRDF 之一是Lambertian模型。它模拟了一个完美的漫反射表面，在半球所有方向上均匀地散射入射照明

1.假设入射光是均匀的

2.根据能量守恒,着色点附近的radiance和irradiance相等

3.BRDF与radiance都是常数,简化式子

4.剩余的就是半球上对的积分: , 结果等于Π

5.因为假设入射能量等于出射能量, 所以BRDF等于1/Π, BRDF等于1/Π代表物体完全不吸收能量的(纯白)

 

我们可以定义一个反射率, 它在0~1之间

BRDF的值等于

Glossy material(BRDF)有光泽的材料

不完全的镜面反射, 略粗糙

 展示图

 

ldeal reflective / refractive material(BSDF*)

理想的反射/折射材料(例如水,玻璃)

 完美镜面反射

 

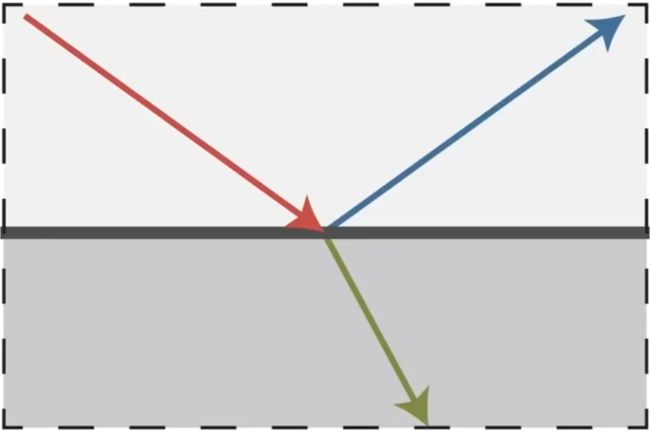
反射公式

入射方向和反射方向的中间一定是物体的法线

ps: Top-down(从上往下看左图)

 效果图

 

BTDF镜面折射

除了从表面反射外，光还可以通过表面折射

光从一个介质进入新介质时会发生折射(有条件)

 

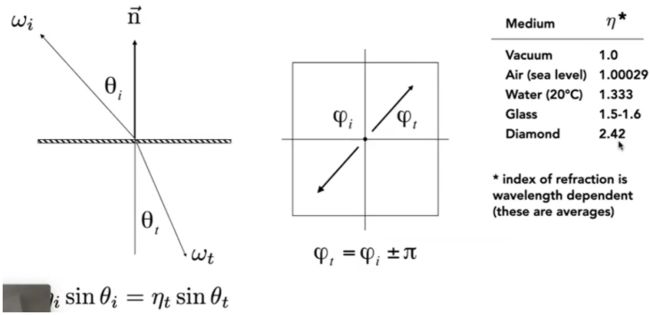
Snell’s Law(折射定律)

传输角度取决于

① 入射光线的折射率(IOR)                         ② 出射光线的折射率(IOR)

 

完全镜面反射:

根据入射光线和物体法线

用折射定律公式推算出

而当根号下的数小于0时, 也就是, 无意义. 进而知道无意义代表无折射现象.

ps: 光密度定义为材料遮光能力的表征

① 当光从光密度较高的介质移动到光密度较小的介质时:, 例如从水到空气, 就没有折射

② 从足够大的角度入射到物体表面的光不会离开原来介质

 从水往空气方向看(光从空气介质到水介质), 在锥形(97.2°)里能看到光, 但是其它地方看不到

BSDF(散射)=BRDF(反射) + BTDF(折射)

菲涅尔项Fresnel Reflection/Term

反射率取决于入射角（和光的偏振）

下图例子：反射率随着入射角的增加而增加

绝缘体(光密度为1.5)的菲尼尔项

x轴是入射角(入射方向与物体法线夹角)

y轴是反射率(反射的能量/全部能量)

例如 :

① 光垂直物体表面(0°)只有接近0.05的能量被反射

② 光平行物体表面(90°)则全部反射

 

 

导体的菲尼尔项

例如: 金属, 镜子

无论是光线垂直于物体表面(0.9~0.93), 还是平行于物体表面(接近1), 反射率都很高(反射出来的能量很高)

导体的折射率是一个复数, 这里没有详细介绍

S polarization: S极化

P polarization: P极化

菲尼尔项公式

一般不考虑出现极化, 直接取中间值

--准确：需要考虑极化

 

--近似值：schlick的近似值(得到广泛应用)

已知准确的函数图, 拟合出一个近似方便计算的函数图

R0: 基准反射率

: 入射角度

 

无论哪个公式, 都是涉及

- n1(介质1的光密度)/n2(介质2的光密度)

- 入射方向, 法线

微表面模型Microfacet Material

为什么我们看不到地球上具体的东西(比如图中照射的是澳大利亚的沙漠, 很粗糙), 而是一个高光?

如何描述这种现象?

 

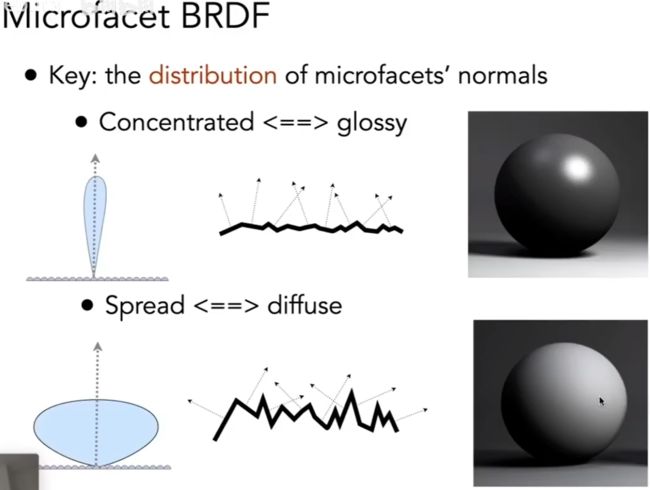
① 粗糙的表面

-宏观：平坦和粗糙

-微观：颠簸和镜面

② 表面的各个元素就像镜子一样

-称为微表面

-每个微表面都有自己的法线

 

关键：微表面法线的分布

法线集中 <==>高光

法线散布 <==>漫反射

 

什么样的微表面反射了 wi 到 wo

（提示：微表面是镜子） 

= 菲涅耳项, 从入射方向i到物体表面的反射率

 = 几何项(自遮挡), 光线被物体粗糙的表面挡住了, 入射方向几乎垂直法线, 导致法线后面的物体接收不到光.

 = 法线分布, 因为微表面是镜子, 遍历有多少微表面法线的向量与中间向量h一致

 

 

效果非常好, 得到广泛应用

当然, 它也是有缺点的, 并不是基于物理, 而且会有diffuse上的缺失.

效果图:

 

各向同性/各向异性材质(BRDFs)

电梯里的金属, 被打磨过的, 所以产生高光为这样.

 

关键: 法线分布的方向性

Isotropic(各向同性): 法线分布具有均匀的方向性

AnIsotropic(各向异性): 法线分布具有明确的方向性

说明从微表面方向性,能看出材质属于各向同性/各向异性

也可以从BRDFs角度分辨是各向同性还是各向异性

各向异性BRDF: 反射取决于方位角, 入射和出射方向相对位置不变,也会影响结果, 结果形成表面的定向微观结构，例如拉丝金属(右球)

各向同性BRDF: 入出射方向相对位置不变,结果不变.(左球)

 

各向异性 BRDF：

① 拉丝金属

② 尼龙(很接近各向同性)

③ 天鹅绒(如果毛均匀得往各个方向去, 它是各向同性)

 但是人可以拨动天鹅绒的纤维, 造成人为的各向异性.

 

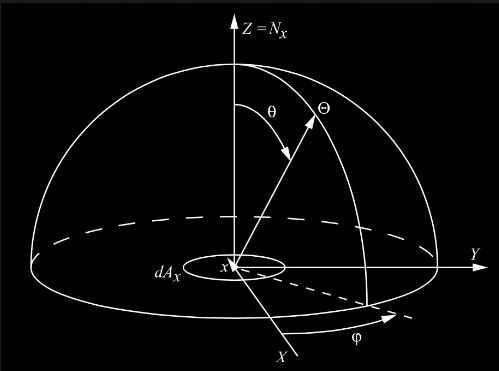
在球坐标中，每一个方向都用两个角度来表示。方位角 φ，仰角 θ。这两个角确定了一个方向 Θ(φ,θ)

 

 

总结: BRDF的性质

1.非负性

2.线性性质(可拆分)

3.互易性: 光传输路径可逆性

4.能量守恒

5.各向同性 vs. 各向异性

各向同性:        

各向异性:        

各向同性可以从四维降到三维, 只考虑相对方位角.

所有的BRDF(不管各向同性还是异性), 根据互易性(光路可逆性), 不用考虑相对方位角的正负和大小.

 

测量BRDFs (Measuring BRDFs)

为什么要测量BRDFs?

避免需要开发/派生模型

-自动包含所有存在的散射效果

可以使用真实世界的材质准确渲染

-可用于产品设计、特殊效果、...

                                                             理论(蓝线) vs实践(other)

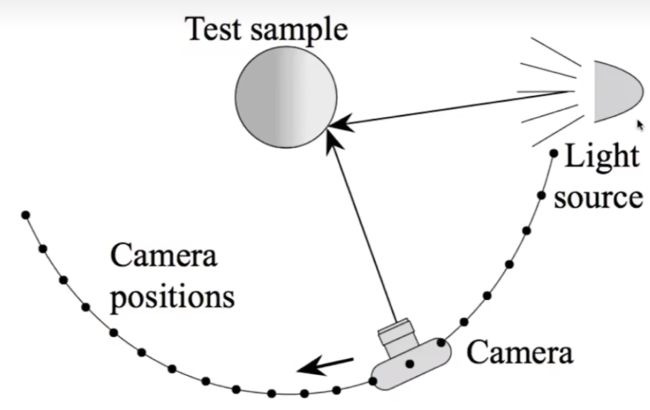
实际测量方法: 基于图像的 BRDF 测量

ps: 对不同的着色点进行光照, 同时也用摄像机不同的角度观察着色点, 得到不同的wi,wo, 然后对不同的结果进行总结BRDF.

测量仪器:

 

一般的测量BRDFs做法：

foreach 传出方向 wo

   用来自 wo 的细光束移动光线以照亮表面

     foreach传入方向 wi

     将传感器从表面移动到方向 wi

     测量入射辐射

提高测量效率：

- 各向同性表面将维度从 4D 降低到 3D

- 光路可逆性将测量次数减少一半

- 聪明的光学系统

测量BRDF的难题

① 掠射角的精确测量

   -由于菲涅耳效应很重要

② 使用足够密集的采样进行测量以捕获高频镜面反射

③ 逆反射

④ 空间变化的反射率

存储测量的 BRDF

理想的存储要求：

① 紧凑的存储

② 测量数据的准确存储

③ 任意方向对的有效评估

④ 可用于重要性抽样的良好分布

表格存储 (Tabular Representation)

将规则间隔的样本存储在

   更好：重新参数化角度以更好地匹配镜面反射

一般需要将测量值重新采样到表中

非常高的存储要求