【超分辨率实验】Matlab-使用深度学习的单图像超分辨率(Single Image Super-Resolution Using Deep Learning)

【超分辨率实验】Matlab-使用深度学习的单图像超分辨率(Single Image Super-Resolution Using Deep Learning)

此示例演示如何训练非常深的超分辨率 VDSR神经网络，并提供预先训练的VDSR网络，使用VDSR网络从单个低分辨率图像估计高分辨率图像。原文链接： Single Image Super-Resolution Using Deep Learning

1 介绍

超分辨率是使用低分辨率图像创建高分辨率图像的过程，本示例考虑单个图像超高分辨率 （SISR），其目标是从一个低分辨率图像中恢复一个高分辨率图像。但是，SISR 是一个不适定问题(ill-posed problem)，因为一个低分辨率图像可以生成几个可能的高分辨率图像。

本示例探索 SISR 的一种深度学习算法，称为Very Deep Super-Resolution （VDSR）。

2 VDSR 网络

VDSR 是一种用于执行单图像超分辨率的卷积神经网络架构，VDSR 网络可以学习低分辨率和高分辨率图像之间的映射，之所以有可能进行这种映射，是因为低分辨率和高分辨率图像具有相似的图像内容，并且主要在高频细节上有所不同。

VDSR 采用残差学习策略，该策略能够估计残差图像。在超分辨率的上下文中，残差图像是高分辨率参考图像与匹配参考图像大小的低分辨率图像之间的差别，其中，匹配大小的过程使用双立方插值的方法进行操作。

VDSR 网络从彩色图像的亮度提取残差图像，图像的亮度通道通过红色、绿色和蓝色像素值的线性组合表示每个像素的亮度。相比之下，图像的两个色度通道（Cb和Cr）是代表颜色差异信息的红色、绿色和蓝色像素值的不同线性组合。VDSR 仅使用亮度通道进行训练，因为人类感知对亮度变化比对颜色变化更敏感。

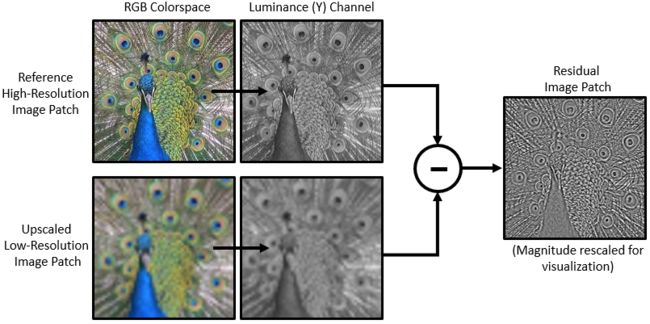
如果Y<高残差>是高分辨率图像的亮度，Y<低残差>是使用双立方插值升级的低分辨率图像，然后 VDSR 网络的输入为Y<低残差>和网络从训练数据学会预测Y<残余> = Y<高残差> - Y<低残差>

在 VDSR 网络学习估计残差图像后，可以通过将估计的残差图像添加到上采样的低分辨率图像，然后将图像转换回 RGB 颜色空间来重建高分辨率图像。

比例因子将参考图像的大小与低分辨率图像的大小关联。随着比例因子的增加，SISR 的重建效果变差，因为低分辨率图像会丢失有关高频图像内容的更多信息，VDSR 使用大感受野解决此问题，本示例使用比例扩增训练具有多个比例因子的 VDSR 网络，缩放扩充可提高较大比例因子的结果，因为网络可以从较小的比例因子中利用图像上下文。

3 实验准备阶段

3.1 下载训练和测试数据

下载 IAPR TC-12 基准，它包括 20，000 张静止自然图像 [2]，数据集包括人、动物、城市等的照片，数据文件的大小为 ±1.8 GB。如果不想下载训练数据集，可以通过在命令行键入来加载预先训练的 VDSR 网络。然后，直接转到本示例中的 VDSR 网络执行单图像超分辨率部分。
命令行键入的语句为：load('trainedVDSR-Epoch-100-ScaleFactors-234.mat')

1. 使用帮助程序函数downloadIAPRTC12Data()下载数据。

imagesDir = tempdir;
url = 'http://www-i6.informatik.rwth-aachen.de/imageclef/resources/iaprtc12.tgz';
downloadIAPRTC12Data(url,imagesDir);

2. 本示例将使用 IAPR TC-12 基准数据的一小部分来训练网络。

trainImagesDir = fullfile(imagesDir,'iaprtc12','images','02');
exts = {'.jpg','.bmp','.png'};
pristineImages = imageDatastore(trainImagesDir,'FileExtensions',exts);

3. 列出训练图像的数量。

numel(pristineImages.Files)

3.2 准备训练数据

1. 要创建训练数据集，先要生成由上采样图像和相应的剩余图像组成的图像对。upsampledDirName表示上采样的图像、residualDirName表示网络响应的计算残差图像作为 MAT 文件存储在磁盘上。

upsampledDirName = [trainImagesDir filesep 'upsampledImages'];
residualDirName = [trainImagesDir filesep 'residualImages'];

2. 使用帮助器函数createVDSRTrainingSet预处理训练数据，帮助器函数对中的每个原始图像执行这些操作：

• 将图像转换为 YCbCr 颜色空间
• 按不同比例因子缩小亮度 （Y） 通道以创建示例低分辨率图像，然后使用双立方插值将图像调整为原始大小
• 计算原始图像和调整大小的图像之间的差值。
• 将调整大小和剩余映像保存到磁盘。

scaleFactors = [2 3 4];
createVDSRTrainingSet(pristineImages,scaleFactors,upsampledDirName,residualDirName);

3.3 为训练集定义预处理管道(pipeline)

1. 网络输入是使用双立方插值进行上采样的低分辨率图像，所需的网络响应是残差图像。upsampledImages创建从输入图像文件集合调用的图像数据存储；residualImagesmat创建从计算的剩余图像文件集合调用的图像数据存储。两个数据存储都需要一个帮助器函数Read ，才能从图像文件中读取图像数据。

upsampledImages = imageDatastore(upsampledDirName,'FileExtensions','.mat','ReadFcn',@matRead);
residualImages = imageDatastore(residualDirName,'FileExtensions','.mat','ReadFcn',@matRead);

2. 创建一个用于指定数据扩充参数的imageDataAugmenter（深度学习工具箱）。在训练期间使用数据扩充来更改训练数据，从而有效地增加可用的训练数据量。在这里，增强器指定随机旋转90 度和 x 方向的随机反射。

augmenter = imageDataAugmenter( ...
    'RandRotation',@()randi([0,1],1)*90, ...
    'RandXReflection',true);

1. 创建一个随机的PatchExtraction数据存储，从上采样和剩余图像数据存储中执行随机补丁提取。修补程序提取是从单个较大图像中提取大量小图像修补程序或切片的过程。这种类型的数据增强常用于图像到图像回归问题，其中许多网络体系结构可以基于非常小的输入图像大小进行训练。这意味着可以从原始训练集的每个全尺寸映像中提取大量补丁，从而大大增加训练集的大小。

patchSize = [41 41];
patchesPerImage = 64;
dsTrain = randomPatchExtractionDatastore(upsampledImages,residualImages,patchSize, ...
    "DataAugmentation",augmenter,"PatchesPerImage",patchesPerImage);

2. 生成的数据存储在epoch的每个迭代中向网络提供小批量数据。disp()预览从数据存储的读取结果。

inputBatch = preview(dsTrain);
disp(inputBatch)

4 设置网络训练数据

4.1 设置 VDSR 图层

此示例使用深度学习工具箱中的 41 个独立图层定义 VDSR 网络，包括：

• 图像输入层（深度学习工具箱） - 图像输入层
• 卷积 2dLayer （深度学习工具箱） - 卷积神经网络的二维卷积层
• reluLayer（深度学习工具箱） - 已纠正的线性单元 （ReLU） 层
• 回归层（深度学习工具箱） - 神经网络的回归输出层

第一层 在图像补丁上操作。修补程序大小基于网络接受字段，即影响网络中最顶层响应的空间图像区域。理想情况下，网络接受域与图像大小相同，以便该字段可以看到图像中的所有高级要素。在这种情况下，对于具有D卷积层的网络，imageInputLayer接受域是 （2D+1）

1. VDSR 有 20 个卷积层，因此接收字段和图像补丁大小为 41x41。图像输入层接受具有一个通道的图像，因为 VDSR
   仅使用亮度通道进行训练。

networkDepth = 20;
firstLayer = imageInputLayer([41 41 1],'Name','InputLayer','Normalization','none');

2. 图像输入层后跟一个二维卷积层，其中包含 64 个大小为 3 比 3的滤波器。小批处理大小确定筛选器数。padding每个卷积层的输入，使要素在每次卷积后保持与输入相同的大小，将权重初始化为随机值，以便神经元学习中存在不对称，每个卷积层后跟一个ReLU 层，在网络中引入非线性。

convLayer = convolution2dLayer(3,64,'Padding',1, ...
    'WeightsInitializer','he','BiasInitializer','zeros','Name','Conv1');

3. 指定 ReLU 图层。

relLayer = reluLayer('Name','ReLU1');

1. 中间层包含 18 个交替卷积和整流线性单位层。每个卷积层包含 64 个大小为 3 比 3 到 64 的滤波器，其中滤波器在 64 个通道的 3-3 空间区域上工作，每个卷积层后跟一个ReLU 层。

middleLayers = [convLayer relLayer];
for layerNumber = 2:networkDepth-1
    convLayer = convolution2dLayer(3,64,'Padding',[1 1], ...
        'WeightsInitializer','he','BiasInitializer','zeros', ...
        'Name',['Conv' num2str(layerNumber)]);
    
    relLayer = reluLayer('Name',['ReLU' num2str(layerNumber)]);
    middleLayers = [middleLayers convLayer relLayer];    
end

2. 倒数第二层是一个卷积层，其大小为 3 比 3 到 64 的单个滤镜可重建图像。

convLayer = convolution2dLayer(3,1,'Padding',[1 1], ...
    'WeightsInitializer','he','BiasInitializer','zeros', ...
    'NumChannels',64,'Name',['Conv' num2str(networkDepth)]);

3. 最后一层是回归层而不是 ReLU 图层。回归层计算残差图像和网络预测之间的均方误差。

finalLayers = [convLayer regressionLayer('Name','FinalRegressionLayer')];

4. 连接所有图层以形成 VDSR 网络。

layers = [firstLayer middleLayers finalLayers];

5. 或者，可以使用帮助器函数vdsrLayers创建 VDSR 图层。

layers = vdsrLayers;

4.2 指定训练选项

1. 使用随机梯度下降与动量 （SGDM） 优化训练网络。使用训练选项（深度学习工具箱）功能指定SGDM的超参数设置。学习率初值为0.1，每 10 个epoch降低 10 倍，训练100个epoch。

maxEpochs = 100;
epochIntervals = 1;
initLearningRate = 0.1;
learningRateFactor = 0.1;
l2reg = 0.0001;
miniBatchSize = 64;

2. 培训深度网络非常耗时，通过指定高学习率可以加速培训，但是，这可能会导致网络梯度爆炸或无法控制地增长，从而阻止网络成功训练。若要将渐变保持在有意义的范围内，指定为启用渐变剪裁GradientThreshold和GradientThresholdMethod，并指定使用渐变的 L2 规范。

options = trainingOptions('sgdm', ...
    'Momentum',0.9, ...
    'InitialLearnRate',initLearningRate, ...
    'LearnRateSchedule','piecewise', ...
    'LearnRateDropPeriod',10, ...
    'LearnRateDropFactor',learningRateFactor, ...
    'L2Regularization',l2reg, ...
    'MaxEpochs',maxEpochs, ...
    'MiniBatchSize',miniBatchSize, ...
    'GradientThresholdMethod','l2norm', ...
    'GradientThreshold',0.01, ...
    'Plots','training-progress', ...
    'Verbose',false);

4.3 训练网络

1. 配置训练选项和随机修补程序提取数据存储后，使用训练网络doTraining功能对 VDSR 网络进行训练。 若要训练网络，需将以下代码中的参数设置为true 。如果将参数保留为false，则示例返回经过预先训练的 VDSR 网络，该网络已经过训练，可对比例因子 2、3 和 4 的超分辨率图像进行训练。

doTraining = false;
if doTraining
    modelDateTime = datestr(now,'dd-mmm-yyyy-HH-MM-SS');
    net = trainNetwork(dsTrain,layers,options);
    save(['trainedVDSR-' modelDateTime '-Epoch-' num2str(maxEpochs*epochIntervals) '-ScaleFactors-' num2str(234) '.mat'],'net','options');
else
    load('trainedVDSR-Epoch-100-ScaleFactors-234.mat');
end

5 使用 VDSR 网络执行单图像超分辨率

若要使用 VDSR 网络执行单个图像超分辨率 （SISR），按照此示例的其余步骤操作。本示例的其余部分演示如何：

• 从高分辨率参考图像创建低分辨率样本图像。
• 使用双立方插值对低分辨率图像执行 SISR，这是一种不依赖深度学习的传统图像处理解决方案。
• 使用 VDSR 神经网络对低分辨率图像执行 SISR。
• 使用双立方插值和 VDSR 直观地比较重建的高分辨率图像。
• 通过量化图像与高分辨率参考图像的相似性来评估超解析图像的质量。

5.1 创建示例低分辨率图像

1. 创建低分辨率图像，用于使用深度学习将超分辨率结果与使用双立方插值等传统图像处理技术的结果进行比较。测试数据集包含 21 个未扭曲的图像，这些图像在图像处理工具箱中将图像加载到testImagesimageDatastore中。

exts = {'.jpg','.png'};
fileNames = {'sherlock.jpg','car2.jpg','fabric.png','greens.jpg','hands1.jpg','kobi.png', ...
    'lighthouse.png','micromarket.jpg','office_4.jpg','onion.png','pears.png','yellowlily.jpg', ...
    'indiancorn.jpg','flamingos.jpg','sevilla.jpg','llama.jpg','parkavenue.jpg', ...
    'peacock.jpg','car1.jpg','strawberries.jpg','wagon.jpg'};
filePath = [fullfile(matlabroot,'toolbox','images','imdata') filesep];
filePathNames = strcat(filePath,fileNames);
testImages = imageDatastore(filePathNames,'FileExtensions',exts);

2. 将测试图像显示为蒙太奇（montage）。

montage(testImages)

3. 选择要用作超分辨率参考图像的图像之一，您可以选择使用自己的高分辨率图像作为参考图像。

indx = 1; % Index of image to read from the test image datastore
Ireference = readimage(testImages,indx);
Ireference = im2double(Ireference);
imshow(Ireference)
title('High-Resolution Reference Image')

4. 使用缩放系数为 0.25 的imresize创建高分辨率参考图像的低分辨率版本，图像的高频分量在向下缩放过程中丢失。

scaleFactor = 0.25;
Ilowres = imresize(Ireference,scaleFactor,'bicubic');
imshow(Ilowres)
title('Low-Resolution Image')

5.2 使用双立方插值提高图像分辨率

1. 在没有深度学习的情况下提高图像分辨率的标准方法是使用双立方插值。使用双立方插值来升级低分辨率图像，使生成的高分辨率图像的大小与参考图像的大小相同。

[nrows,ncols,np] = size(Ireference);
Ibicubic = imresize(Ilowres,[nrows ncols],'bicubic');
imshow(Ibicubic)
title('High-Resolution Image Obtained Using Bicubic Interpolation')

5.3 使用预训练的 VDSR 网络提高图像分辨率

回想一下，，因为人类感知对亮度变化比对颜色变化更敏感。

1. VDSR 仅使用图像的亮度通道进行训练，实验中使用rgb2ycbcr函数将低分辨率图像从 RGB 颜色空间转换为亮度(Iy)和色度(Icb、Icr)通道。

Iycbcr = rgb2ycbcr(Ilowres);
Iy = Iycbcr(:,:,1);
Icb = Iycbcr(:,:,2);
Icr = Iycbcr(:,:,3);

2. 使用双立方插值提升亮度和两个色度通道。上采样的色度通道Icb_bicubic和Icr_bicubic不需要进一步处理。

Iy_bicubic = imresize(Iy,[nrows ncols],'bicubic');
Icb_bicubic = imresize(Icb,[nrows ncols],'bicubic');
Icr_bicubic = imresize(Icr,[nrows ncols],'bicubic');

3. 通过训练好的 VDSR 网络传递高档亮度组件Iy_bicubic。观察最终图层（回归层）中的activation，网络的输出是所需的残差图像。

Iresidual = activations(net,Iy_bicubic,41);
Iresidual = double(Iresidual);
imshow(Iresidual,[])
title('Residual Image from VDSR')

4. 将剩余图像添加到高档亮度组件，以获得高分辨率 VDSR 亮度分量。

Isr = Iy_bicubic + Iresidual;

5. 将高分辨率 VDSR 亮度组件与高档彩色元件串联在一起，使用ycbcr2rgb函数将图像转换为 RGB 颜色空间。

Ivdsr = ycbcr2rgb(cat(3,Isr,Icb_bicubic,Icr_bicubic));
imshow(Ivdsr)
title('High-Resolution Image Obtained Using VDSR')

5.4 视觉和定量比较

1. 为了更好地了解高分辨率图像，请检查每个图像中的一个小区域。使用格式的矢量（x y宽度高度）指定感兴趣区域 （ROI）。这些元素定义左上角的 x 坐标和 y 坐标，以及 ROI 的宽度和高度。

roi = [320 30 480 400];

2. 将高分辨率图像裁剪为此 ROI，并显示结果为蒙太奇。VDSR 图像比使用双立方插值创建的高分辨率图像具有更清晰的细节和更清晰的边缘。

montage({imcrop(Ibicubic,roi),imcrop(Ivdsr,roi)})
title('High-Resolution Results Using Bicubic Interpolation (Left) vs. VDSR (Right)');

3. 使用图像质量指标使用双立方插值定量比较高分辨率图像与 VDSR 图像。参考图像是原始高分辨率图像Ireference。根据参考图像测量每个图像的峰值信噪比 （PSNR），较大的 PSNR 值通常表示图像质量更好。

bicubicPSNR = psnr(Ibicubic,Ireference)
vdsrPSNR = psnr(Ivdsr,Ireference)

4. 测量每个图像的结构相似性指数 （SSIM）。SSIM 评估图像三个特征的视觉冲击：亮度、对比度和结构，以及参考图像。SSIM 值越接近 1，测试图像与参考图像的同意性越好。

bicubicSSIM = ssim(Ibicubic,Ireference)
vdsrSSIM = ssim(Ivdsr,Ireference)

5. 使用自然性图像质量评估器 （NIQE） 测量感知图像质量。较小的 NIQE 分数表示感知质量更好。

bicubicNIQE = niqe(Ibicubic)
vdsrNIQE = niqe(Ivdsr)

6. 计算比例因子 2、3 和 4 的整个测试图像集的平均 PSNR 和 SSIM。为简单起见，可以使用帮助器函数superResolutionMetrics计算平均指标。

scaleFactors = [2 3 4];
superResolutionMetrics(net,testImages,scaleFactors);

Results for Scale factor 2

Average PSNR for Bicubic = 31.809683
Average PSNR for VDSR = 31.921784
Average SSIM for Bicubic = 0.938194
Average SSIM for VDSR = 0.949404

Results for Scale factor 3

Average PSNR for Bicubic = 28.170441
Average PSNR for VDSR = 28.563952
Average SSIM for Bicubic = 0.884381
Average SSIM for VDSR = 0.895830

Results for Scale factor 4

Average PSNR for Bicubic = 27.010839
Average PSNR for VDSR = 27.837260
Average SSIM for Bicubic = 0.861604
Average SSIM for VDSR = 0.877132
VDSR 在每个比例因子的指标分数比双立方插值更好。

引用

• [1] Kim, J., J. K. Lee, and K. M. Lee. “Accurate Image Super-Resolution Using Very Deep Convolutional Networks.” Proceedings of the IEEE® Conference on Computer Vision and Pattern Recognition.2016, pp. 1646-1654.
  [2] Grubinger, M., P. Clough, H. Müller, and T. Deselaers. “The IAPR TC-12 Benchmark: A New Evaluation Resource for Visual Information Systems.” Proceedings of the OntoImage 2006 Language Resources For Content-Based Image Retrieval. Genoa, Italy. Vol. 5, May 2006, p. 10.
  [3] He, K., X. Zhang, S. Ren, and J. Sun. “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNe Classification.” Proceedings of the IEEE International Conference on Computer Vision, 2015, pp. 1026-1034.