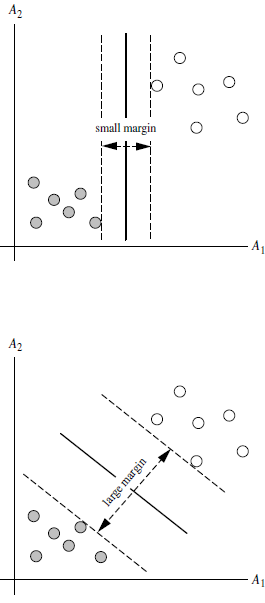
1、线性可区分(linear separable)和线性不可区分(linear inseparable)两种情况。
SVM算法寻找两类的超平面(hyper plane),使边际(margin)最大。也就是找最大超平面MMH(Max Margin Hyperplane )
超平面定义公式:WX+b=0
W={w1,w2,w3,……}为Weight Vector 权重向量 ;
X为训练实例;
b为偏向Bias
二维情况下:X=(x1,x2)
超平面方程:w1*x1+w2*x2+w0=0
超平面两侧:w1*x1+w2*x2+w0>0
w1*x1+w2*x2+w0<0
调整weight,用超平面定义边际的两边:H1=w1*x1+w2*x2+w0>=1; yi=1
H2=w1*x1+w2*x2+w0<=-1; yi=-1
所以: yi*(w1*x1+w2*x2+w0)>=1;
所有坐落在边际的两边的超平面上被称为支持向量Support Vector,
分界的超平面离边界上任意一点距离为 1/||W||,最大边际为2/||W||
Max Margin Hyperplane表示公式:
yi是支持向量点Xi的类别标记。XT是测试实例。ai和b0为单一数值参数,l为支持向量的个数。
1、训练好的模型的算法复杂度是由支持向量的个数决定,而不是由数据的维度决定,所以SVM不太容易产生过拟合overfitting
2、SVM训练出的模型完全依赖于支持向量,即使训练集中所有非支持向量的点全部去除,仍然会训练处一样的模型。
3、一个SVM如果训练得到的支持向量的个数比较少,SVM训练的模型就容易被泛化。
from sklearn import svm
x=[[2,0],[1,1],[2,3]]#特征向量
y=[0,0,1]#特征对应的label
clf=svm.SVC(kernel='linear')
clf.fit(x,y)
print(clf)
print(clf.support_vectors_)#支持向量
print(clf.support_)#支持向量在x中的索引
print(clf.n_support_)#针对每个标签label找到了几个支持向量
print(clf.predict([[2,0]]))#预测这个点属于哪一类标签label