(六)学习笔记:动手学深度学习(自动求导)
自动求导
- 1.链式法则
-
- 1.1向量的链式法则
-
- 1.1.1实例一
- 1.1.2实例二
- 2.计算图
- 3.自动求导的两种模式
-
- 3.1正向累积和反向累积
- 3.2反向累积总结
- 3.3复杂度
-
- 3.3.1反向累积和正向累积复杂度的对比
- 4.自动微分
-
- 4.1一个简单的例子
- 4.2 非标量变量的反向传播
- 4.3 分离计算
- 4.4 Python控制流的梯度计算
- 4.5小结
- 4.6练习
1.链式法则
这是因为在深度学习中,多元函数通常是复合(composite)的,
所以我们可能没法应用上述任何规则来微分这些函数。
幸运的是,链式法则使我们能够微分复合函数。
让我们先考虑单变量函数。假设函数 y = f ( u ) y=f(u) y=f(u)和 u = g ( x ) u=g(x) u=g(x)都是可微的,根据链式法则:
d y d x = d y d u d u d x . \frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}. dxdy=dudydxdu.
现在让我们把注意力转向一个更一般的场景,即函数具有任意数量的变量的情况。
假设可微分函数 y y y有变量 u 1 , u 2 , … , u m u_1, u_2, \ldots, u_m u1,u2,…,um,其中每个可微分函数 u i u_i ui都有变量 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn。
注意, y y y是 x 1 , x 2 , … , x n x_1, x_2, \ldots, x_n x1,x2,…,xn的函数。
对于任意 i = 1 , 2 , … , n i = 1, 2, \ldots, n i=1,2,…,n,链式法则给出:
d y d x i = d y d u 1 d u 1 d x i + d y d u 2 d u 2 d x i + ⋯ + d y d u m d u m d x i \frac{dy}{dx_i} = \frac{dy}{du_1} \frac{du_1}{dx_i} + \frac{dy}{du_2} \frac{du_2}{dx_i} + \cdots + \frac{dy}{du_m} \frac{du_m}{dx_i} dxidy=du1dydxidu1+du2dydxidu2+⋯+dumdydxidum
1.1向量的链式法则
1.1.1实例一
1.1.2实例二
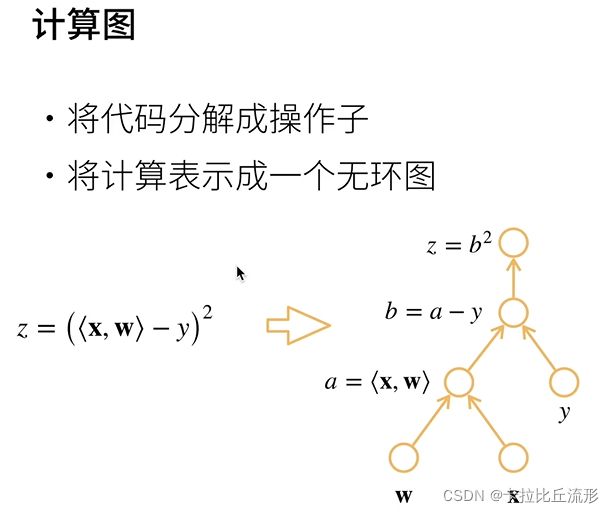
2.计算图
3.自动求导的两种模式
3.1正向累积和反向累积
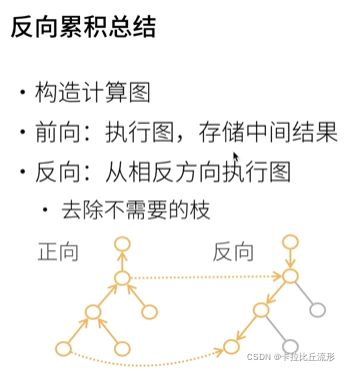
3.2反向累积总结
3.3复杂度
3.3.1反向累积和正向累积复杂度的对比
4.自动微分
求导是几乎所有深度学习优化算法的关键步骤。虽然求导的计算很简单,只需要一些基本的微积分。但对于复杂的模型,手工进行更新是一件很痛苦的事情(而且经常容易出错)。
深度学习框架通过自动计算导数,即自动微分(automatic differentiation)来加快求导。
实际中,根据我们设计的模型,系统会构建一个计算图(computational graph),来跟踪计算是哪些数据通过哪些操作组合起来产生输出。
自动微分使系统能够随后反向传播梯度。
这里,反向传播(backpropagate)意味着跟踪整个计算图,填充关于每个参数的偏导数。
4.1一个简单的例子
作为一个演示例子,(假设我们想对函数 y = 2 x ⊤ x y=2\mathbf{x}^{\top}\mathbf{x} y=2x⊤x关于列向量 x \mathbf{x} x求导)。
首先,我们创建变量x并为其分配一个初始值。
import torch
x = torch.arange(4.0)
x
tensor([0., 1., 2., 3.])
[在我们计算 y y y关于 x \mathbf{x} x的梯度之前,我们需要一个地方来存储梯度。]
重要的是,我们不会在每次对一个参数求导时都分配新的内存。
因为我们经常会成千上万次地更新相同的参数,每次都分配新的内存可能很快就会将内存耗尽。
注意,一个标量函数关于向量 x \mathbf{x} x的梯度是向量,并且与 x \mathbf{x} x具有相同的形状。
x.requires_grad_(True) # 等价于 `x = torch.arange(4.0, requires_grad=True)`
#说明当前量需要在计算中保留对应的梯度信息
x.grad # 默认值是None
(现在让我们计算 y y y。)
y = 2 * torch.dot(x, x)
y
tensor(28., grad_fn=)
x是一个长度为4的向量,计算x和x的点积,得到了我们赋值给y的标量输出。
接下来,我们[通过调用反向传播函数来自动计算y关于x每个分量的梯度],并打印这些梯度。
y.backward()
x.grad
tensor([ 0., 4., 8., 12.])
函数 y = 2 x ⊤ x y=2\mathbf{x}^{\top}\mathbf{x} y=2x⊤x关于 x \mathbf{x} x的梯度应为 4 x 4\mathbf{x} 4x。让我们快速验证这个梯度是否计算正确。
x.grad == 4 * x
tensor([True, True, True, True])
[现在让我们计算x的另一个函数。]
# 在默认情况下,PyTorch会累积梯度,我们需要清除之前的值
x.grad.zero_()
y = x.sum()
y.backward()
x.grad
ensor([1., 1., 1., 1.])
4.2 非标量变量的反向传播
当y不是标量时,向量y关于向量x的导数的最自然解释是一个矩阵。
对于高阶和高维的y和x,求导的结果可以是一个高阶张量。
然而,虽然这些更奇特的对象确实出现在高级机器学习中(包括[深度学习中]),
但当我们调用向量的反向计算时,我们通常会试图计算一批训练样本中每个组成部分的损失函数的导数。
这里(,我们的目的不是计算微分矩阵,而是单独计算批量中每个样本的偏导数之和。)
# 对非标量调用`backward`需要传入一个`gradient`参数,该参数指定微分函数关于`self`的梯度。
# 在我们的例子中,我们只想求偏导数的和,所以传递一个1的梯度是合适的
x.grad.zero_()
y = x * x
# 等价于y.backward(torch.ones(len(x)))
y.sum().backward()
x.grad
tensor([0., 2., 4., 6.])
4.3 分离计算
有时,我们希望[将某些计算移动到记录的计算图之外]。
例如,假设y是作为x的函数计算的,而z则是作为y和x的函数计算的。
想象一下,我们想计算z关于x的梯度,但由于某种原因,我们希望将y视为一个常数,
并且只考虑到x在y被计算后发挥的作用。
在这里,我们可以分离y来返回一个新变量u,该变量与y具有相同的值,
但丢弃计算图中如何计算y的任何信息。
换句话说,梯度不会向后流经u到x。
因此,下面的反向传播函数计算z=u*x关于x的偏导数,同时将u作为常数处理,
而不是z=x*x*x关于x的偏导数。
x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u
tensor([True, True, True, True])
由于记录了y的计算结果,我们可以随后在y上调用反向传播,
得到y=x*x关于的x的导数,即2*x。
x.grad.zero_()
y.sum().backward()
x.grad == 2 * x
tensor([True, True, True, True])
4.4 Python控制流的梯度计算
使用自动微分的一个好处是:
[即使构建函数的计算图需要通过Python控制流(例如,条件、循环或任意函数调用),我们仍然可以计算得到的变量的梯度]。
在下面的代码中,while循环的迭代次数和if语句的结果都取决于输入a的值。
def f(a):
b = a * 2
while b.norm() < 1000:
b = b * 2
if b.sum() > 0:
c = b
else:
c = 100 * b
return c
计算梯度
a = torch.randn(size=(), requires_grad=True)
d = f(a)
d.backward()
我们现在可以分析上面定义的f函数。
请注意,它在其输入a中是分段线性的。
换言之,对于任何a,存在某个常量标量k,使得f(a)=k*a,其中k的值取决于输入a。
因此,我们可以用d/a验证梯度是否正确。
a.grad == d / a
tensor(True)
4.5小结
- 链式法则使我们能够微分复合函数。
- 深度学习框架可以自动计算导数:我们首先将梯度附加到想要对其计算偏导数的变量上。然后我们记录目标值的计算,执行它的反向传播函数,并访问得到的梯度。
4.6练习
- 为什么计算二阶导数比一阶导数的开销要更大?
答:二阶导数是在一阶导数的基础上进行求值的,而且分子分母都变得很小,对中间结果数值精度要求更高。 - 在运行反向传播函数之后,立即再次运行它,看看会发生什么。
答:会报错,由于中间结果已经被清除了。
RuntimeError: Trying to backward through the graph a second time,
but the saved intermediate results have already been freed.
Specify retain_graph=True when calling .backward() or autograd.grad() the first time.
- 在控制流的例子中,我们计算
d关于a的导数,如果我们将变量a更改为随机向量或矩阵,会发生什么?
RuntimeError: grad can be implicitly created only for scalar outputs
- 重新设计一个求控制流梯度的例子,运行并分析结果。
import torch
def f(a):
b = a
while b.norm() < 1000:
b = b * 4
if b.sum() > 0:
c = b/2
else:
c = 100 * b
return c
a = torch.randn(size=(3,1), requires_grad=True)
d = f(a)
d.sum().backward()
a.grad == d / a
tensor([[True],
[True],
[True]])
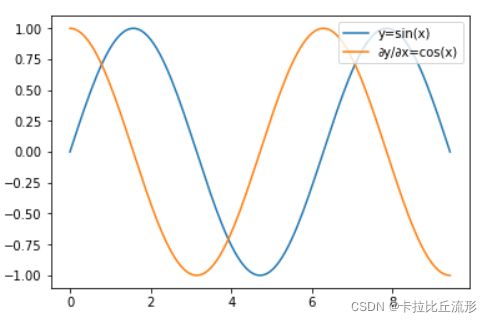
- 使 f ( x ) = sin ( x ) f(x)=\sin(x) f(x)=sin(x),绘制 f ( x ) f(x) f(x)和 d f ( x ) d x \frac{df(x)}{dx} dxdf(x)的图像,其中后者不使用 f ′ ( x ) = cos ( x ) f'(x)=\cos(x) f′(x)=cos(x)。
import torch
import matplotlib.pyplot as plt
import numpy as np
x = torch.linspace(0, 3*np.pi, 128)
x.requires_grad_(True)#说明当前量需要在计算中保留对应的梯度信息
y = torch.sin(x) # y = sin(x)
y.sum().backward()#通过调用反向传播函数来自动计算y关于x每个分量的梯度
#detach的方法,将variable参数从网络中隔离开,不参与参数更新
plt.plot(x.detach(), y.detach(), label='y=sin(x)')
plt.plot(x.detach(), x.grad, label='∂y/∂x=cos(x)') # dy/dx = cos(x)
plt.legend(loc='upper right')
plt.show()