相关系数
相关系数
相关系数(Correlation coefficient)
什么是相关系数
相关表和相关图可反映两个变量之间的相互关系及其相关方向,但无法确切地表明两个变量之间相关的程度。
著名统计学家卡尔·皮尔逊设计了统计指标——相关系数。相关系数是用以反映变量之间相关关系密切程度的统计指标。相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度;着重研究线性的单相关系数。
依据相关现象之间的不同特征,其统计指标的名称有所不同。如将反映两变量间线性相关关系的统计指标称为相关系数(相关系数的平方称为判定系数);将反映两变量间曲线相关关系的统计指标称为非线性相关系数、非线性判定系数;将反映多元线性相关关系的统计指标称为复相关系数、复判定系数等。
相关系数的几种定义
相关关系是一种非确定性的关系,相关系数是研究变量之间线性相关程度的量。由于研究对象的不同,相关系数有如下几种定义方式。
简单相关系数:又叫相关系数或线性相关系数,一般用字母P 表示,是用来度量变量间的线性关系的量。
复相关系数:又叫多重相关系数。复相关是指因变量与多个自变量之间的相关关系。例如,某种商品的季节性需求量与其价格水平、职工收入水平等现象之间呈现复相关关系。
典型相关系数:是先对原来各组变量进行主成分分析,得到新的线性关系的综合指标,再通过综合指标之间的线性相关系数来研究原各组变量间相关关系。
相关系数的性质[1]
(1) ;
;
(2)定理: | ρXY | = 1的充要条件是,存在常数a,b,使得 ;
;
相关系数ρXY取值在-1到1之问,ρXY = 0时,
称X,Y不相关; | ρXY | = 1时,称X,Y完全相关,此时,X,Y之间具有线性函数关系; | ρXY | < 1时,X的变动引起Y的部分变动,ρXY的绝对值越大,X的变动引起Y的变动就越大, | ρXY | > 0.8时称为高度相关,当 ,即 | ρXY | < 0.3时,称为低度相关,其他为中度相关。
,即 | ρXY | < 0.3时,称为低度相关,其他为中度相关。
(3)推论:若Y=a+bX,则有

证明: 令E(X) = μ,D(X) = σ2
则E(Y) = bμ + a,D(Y) = b2σ2
E(XY) = E(aX + bX2) = aμ + b(σ2 + μ2)
Cov(X,Y) = E(XY) − E(X)E(Y) = bσ2
若b≠0,则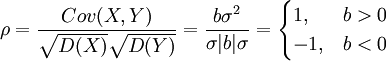
若b=0,则ρXY = 0。
相关系数的计算方法
相关系数的公式如下:[2]
 (1)
(1)
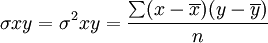
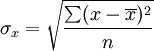

 (2)
(2)
 (3)
(3)
![=\frac{n^2[\frac{\sum xy}{n}-]}{\frac{\sum x}{n}-\frac{\sum y}{n}}{\sqrt{n^2[\frac{\sum x^2}{n}-(\frac{\sum x}{n})^2]\cdot\sqrt n^2[\frac{\sum y^2}{n}-(\frac{\sum y}{n})^2]}}](http://img.e-com-net.com/image/product/600d13963444481cb177f8d6f01d72db.png) (4)
(4)
 (5)
(5)
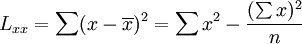
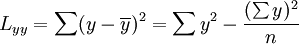
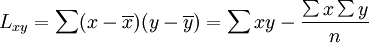
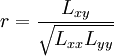
相关系数的值介于–1与+1之间,即–1≤r≤+1。其性质如下:
- 当r>0时,表示两变量正相关,r<0时,两变量为负相关。
- 当|r|=1时,表示两变量为完全线性相关,即为函数关系。
- 当r=0时,表示两变量间无线性相关关系。
- 当0<|r|<1时,表示两变量存在一定程度的线性相关。且|r|越接近1,两变量间线性关系越密切;|r|越接近于0,表示两变量的线性相关越弱。
- 一般可按三级划分:|r|<0.4为低度线性相关;0.4≤|r|<0.7为显著性相关;0.7≤|r|<1为高度线性相关。
例:某财务软件公司在全国有许多代理商,为研究它的财务软件产品的广告投入与销售额的关系,统计人员随机选择10家代理商进行观察,搜集到年广告投入费和月平均销售额的数据,并编制成相关表,见表1:
表1 广告费与月平均销售额相关表 单位:万元
| 年广告费投入 | 月均销售额 |
|---|---|
| 12.5 15.3 23.2 26.4 33.5 34.4 39.4 45.2 55.4 60.9 |
21.2 23.9 32.9 34.1 42.5 43.2 49.0 52.8 59.4 63.5 |
参照表1,可计算相关系数如表2:
| 序号 | 广告投入(万元) x |
月均销售额(万元) y |
x^2 | y2 | xy |
|---|---|---|---|---|---|
| 1 2 3 4 5 6 7 8 9 10 |
12.5 15.3 23.2 26.4 33.5 34.4 39.4 45.2 55.4 60.9 |
21.2 23.9 32.9 34.1 42.5 43.2 49.0 52.8 59.4 63.5 |
156.25 234.09 538.24 696.96 1122.25 1183.36 1552.36 2043.04 3069.16 3708.81 |
449.44 571.21 1082.41 1162.81 1806.25 1866.24 2401.00 2787.84 3528.36 4032.25 |
265.00 365.67 763.28 900.24 1423.75 1486.08 1930.60 2386.56 3290.76 3867.15 |
| 合计 | 346.2 | 422.5 | 14304.52 | 19687.81 | 16679.09 |
-

-
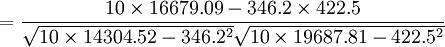
- =0.9942
相关系数为0.9942,说明广告投入费与月平均销售额之间有高度的线性正相关关系。
相关系数的应用[1]
- 1.在 概率论计算中的应用
例1.若将一枚硬币抛n次,X表示n次试验中出现正面的次数,Y表示n次试验中出现反面的次数。计算ρXY。
解:由于X+Y=n,则Y=-X+n,根据相关系数的性质推论,得ρXY = − 1。
例2.已知随机变量X、Y分别服从正态分布N(1,9),N(0,16)且X,Y的相关系数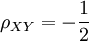
设 ,求证X,Z相互独立。
,求证X,Z相互独立。
证明:由已知得E(X)=1,D(X)=9,E(Y)= 0,D(Y) = 16

由于正态分布的随机变量的线性组合仍然服从正态分布,知Z是正态变量。
根据数学期望的性质有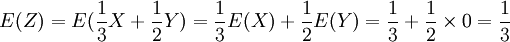
根据方差的性质有 得
得 
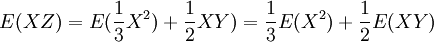
由于 E(XY) = Cov(X,Y) + E(X)E(Y) = − 6,
E(X2) = D(X) + [E(X)]2 = 10

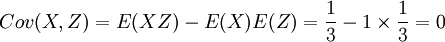
ρXZ = 0,X,Z不相关。
由于正态随机变量的相互独立与互不相关等价,故X,Z相互独立。
因此,一般情况下两个随机变量不相关不一定相互独立。不相关仅指随机变量之问没有线性关系,而相互独立则表明随机变量之间互不影响,没有关系。
- 2.在 企业物流上的应用
【例】一种新产品上市。在上市之前,公司的物流部需把新产品合理分配到全国的10个仓库,新品上市一个月后,要评估实际分配方案与之前考虑的其他分配方案中,是实际分配方案好还是其中尚未使用的分配方案更好,通过这样的评估,可以在下一次的新产品上市使用更准确的产品分配方案,以避免由于分配而产生的积压和断货。表1是根据实际数据所列的数表。
通过计算,很容易得出这3个分配方案中,B的相关系数是最大的,这样就评估到B的分配方案比实际分配方案A更好,在下一次的新产品上市分配计划中,就可以考虑用B这种分配方法来计算实际分配方案。
- 3.在 聚类分析中的应用
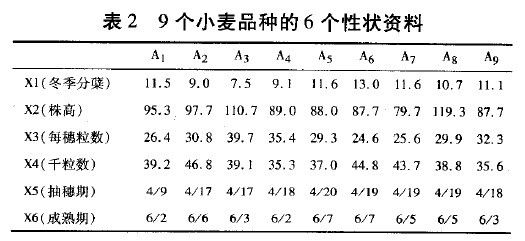
【例】如果有若干个样品,每个样品有n个特征,则相关系数可以表示两个样品问的相似程度。借此,可以对样品的亲疏远近进行距离聚类。例如9个小麦品种(分别用A1,A2,...,A9表示)的6个性状资料见表2,作相关系数计算并检验。
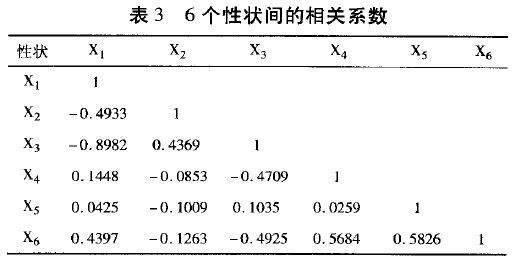
由相关系数计算公式可计算出6个性状间的相关系数,分析及检验结果见表3。由表3可以看出,冬季分蘖与每穗粒数之间呈现负相关(ρ = − 0.8982),即麦冬季分蘖越多,那么每穗的小麦粒数越少,其他性状之间的关系不显著。
相关系数的缺点
需要指出的是,相关系数有一个明显的缺点,即它接近于1的程度与数据组数n相关,这容易给人一种假象。因为,当n较小时,相关系数的波动较大, 对有些样本相关系数的绝对值易接近于1;当n较大时,相关系数的绝对值容易偏小。特别是当n=2时,相关系数的绝对值总为1。因此在样本容量n较小时,我们仅凭相关系数较大就判定变量x与y之间有密切的线性关系是不妥当的。
例如,就我国深沪两股市资产负债率与每股收益之间的相关关系做研究。发现1999年资产负债率前40名的上市公司,二者的相关系数为r=–0.6139;资产负债率后20名的上市公司,二者的相关系数r=0.1072;而对于沪、深全部上市公司(基金除外)结果却是,r沪=–0.5509,r深=–0.4361,根据三级划分方法,两变量为显著性相关。这也说明仅凭r的计算值大小判断相关程度有一定的缺陷。