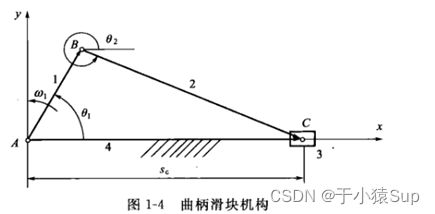
Matlab学习——曲柄滑块的运动仿真

1、图解法

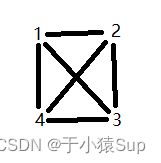
①机构位置分析的图解法

选取适当的长度比例尺
$${\mu }_l=0.6:1$$
选取曲柄l1的铰链中心A 点的位置，

按主动杆
$$\mathrm{r}=60mm$$
连杆
$$l=300mm$$
初始位置
$${\theta }_1=0$$
依次作图确定出滑块的导路位置线$xx$和铰链中心B和C的位置，然后画出连杆2和滑块3的位置BC及C和两处的位置参数 ${\theta }_2$ 和$s$的位置。

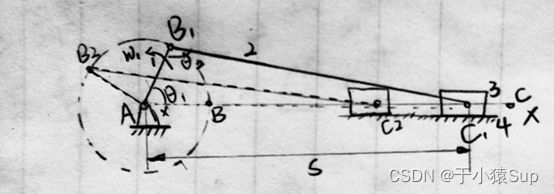
②速度分析的图解法（瞬心法）

如上图所示，有构件数目为4，则瞬心数目为 $C_4^2=6$。构件1和构件2、构件2和构件3、构件1和构件4的瞬心分别是转动副 $p_{12}$、 $p_{23}$、$p_{14}$。构件3和构件4为移动副所以瞬心$p_{34}$在垂直导路的方向无穷远处。根据瞬心多边形法分别求出$p_{13}$、$p_{24}$。

根据速度瞬心定理得
$$v_{p_{13}}={\omega }_1(\overline{p_{14}{p}_{13}}{\mu }_l)$$
则滑块的速度
$$v_3=v_{p_{13}}$$

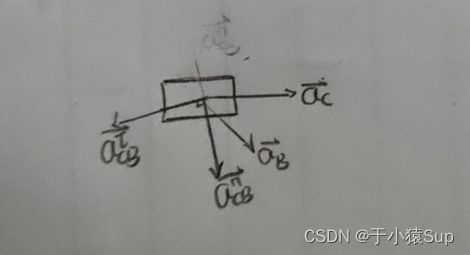
③加速度分析的图解法

所以
$$a_C=a_B+a_{CB}^n+a_{CB}^{\tau }$$
根据速度分析$\frac{{\omega }_2}{{\omega }_1}=\frac{\overline{p_{12}{p}_{14}}}{\overline{p_{12}{p}_{24}}}$,可求出${\omega }_2$。

则 $a_B={{\omega }_1}^2{l}_1(已知)，a_{CB}^n={{\omega }_2}^2{l}_2(已知)，a_{CB}^{\tau }={\alpha }_2{l}_2(大小未知)$

滑块加速度为
$$a_C={\mu }_a\overline{pc}$$

2、solidworks分析法

①滑块线位移曲线

②滑块线速度曲线

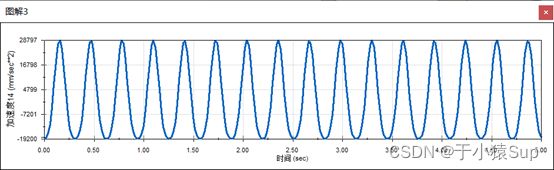
③滑块线加速度曲线

④连杆角位移曲线

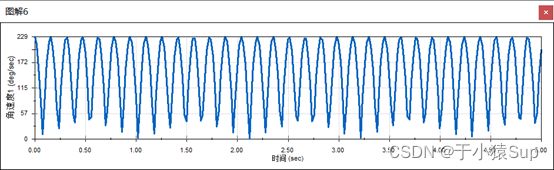
⑤连杆角速度曲线

⑥连杆角加速度曲线

3、解析法

①位置分析

对封闭图形ABCA可知，封闭矢量方程式 （3-1）
$$l1+l2=s$$
转化为复数的形式（3-2）

$$l1e^{i{\theta }_1}+l2e^{i{\theta }_2}=s$$
根据欧拉公式（3-3）
$$e^{{}^{i\theta }}=\cos (\theta )+\sin (\theta )i$$
​

将实部与虚部分离得 （3-4）
$$\begin{array}{l}l1\cos {\theta }_1+l2\cos {\theta }_2=s\\ l1\sin {\theta }_1+l2\sin {\theta }_2=0\end{array}$$
​

由上式得（3-5）
$$\begin{array}{l}{\theta }_2=\arcsin (\frac{-l1\sin {\theta }_1}{l2})\\ s=l1\cos {\theta }_1+l2\cos {\theta }_2\end{array}$$
​

代码相关部分

theta2=asin((e-l1 * sin(theta1))/l2);  

s=l1 * cos(theta1) + l2 * cos(theta2); 

②速度分析

由（3-2）式对时间求一次导得速度关系（3-6）
$$il1{\omega }_1{e}^{i{\theta }_1}+il2{\omega }_2{e}^{i{\theta }_2}=v$$
将虚部与实部分离得(3-7)
$$\begin{array}{l}l1{\omega }_1\cos {\theta }_1+l2{\omega }_2\cos {\theta }_2=0\\ -l1{\omega }_1\sin {\theta }_1-l2{\omega }_2\sin {\theta }_2=v\end{array}$$
用矩阵可表示为(3-8)
$$\left(\begin{array}{cc}l2\sin {\theta }_2& 1\\ -l2\cos {\theta }_2& 0\end{array}\right)\left(\begin{array}{c}{\omega }_2\\ v\end{array}\right)={\omega }_1\left(\begin{array}{c}-l1\sin {\theta }_1\\ l1\cos {\theta }_1\end{array}\right)$$
可根据上式求出角速度 ${\omega }_2$和滑块速度v 。

代码相关部分

A=[l2*sin(theta2), 1; -l2*cos(theta2), 0]; 
B=[-l1*sin(theta1); l1*cos(theta1)];  
% ‘\’求解关于 x 的线性方程组 Ax = B 
%  eg: x=A\B 
omega=A \ (omega1*B);         
omega2=omega(1); 
v=omega(2); 

③加速度分析

由（3-6）式求一次导可得加速度关系式，矩阵表示为（3-9）
$$\left(\begin{array}{cc}l2\sin {\theta }_2& 1\\ -l2\cos {\theta }_2& 0\end{array}\right)\left(\begin{array}{c}{\alpha }_2\\ a\end{array}\right)+\left(\begin{array}{cc}{\omega }_{2}l2\cos {\theta }_2& 0\\ {\omega }_{2}l2\sin {\theta }_2& 0\end{array}\right)\left(\begin{array}{c}{\omega }_2\\ v\end{array}\right)={\omega }_1\left(\begin{array}{c}-{\omega }_{1}l1\cos {\theta }_1\\ -{\omega }_{1}l1\sin {\theta }_1\end{array}\right)$$
代码相关部分

Aa=[omega2*l2*cos(theta2), 0; 
	omega2*l2*sin(theta2), 0];        
Ba= [-omega1*l1*cos(theta1);       
	-omega1*l1*sin(theta1)];      
alpha=A \(-Aa*omega+alpha1*B+omega1*Ba);  
alpha2 = alpha(1); 
a = alpha(2); 

CODE

clear;
r = 60;  % 主动杆杆长
l = 300;  % 连杆杆长
e = 0;  % 偏心距
hd = pi/180;
du = 180/pi;
omega1 = 20; % 主动杆角速度
alpha1 = 0; % 主动杆角加速度

% for循环获取0-4pi构件2角位移、滑块位移、构件2角速度、滑块线速度、构件2角加速度、滑块线加速度
for n1= 1:720
    theta1(n1)=(n1-1)*hd;  % 0-4pi
    [theta2(n1) , s(n1) , omega2(n1), v(n1) , alpha2(n1), a(n1)] = slider_crank(theta1(n1) , omega1, alpha1, r, l, e);
end

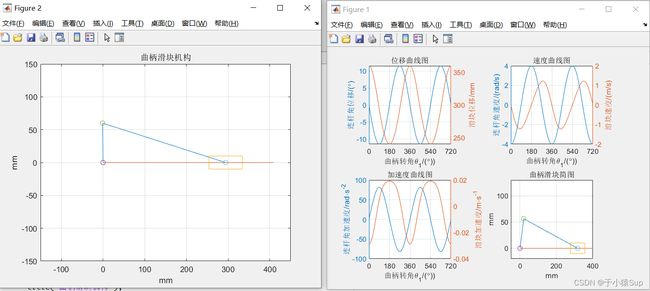
figure(1);
n = 1:720;
% 位移曲线图
subplot(2, 2, 1);
yyaxis left;
plot(theta1*du, theta2*du);
ylabel('连杆角位移/(\circ)');
yyaxis right;
plot(theta1*du, s);
ylabel('滑块位移/mm');
xlabel('曲柄转角\theta_1/(\circ))');
title('位移曲线图');
xlim([0, 720]);
x_new = linspace(0, 720, 5);
xticks(x_new)
grid on;

%速度曲线图
subplot(2,2,2);
yyaxis left;
plot(theta1*du, omega2);
ylabel('连杆角速度/(rad/s)');
yyaxis right;
plot(theta1*du, v/1000);
ylabel('滑块速度/(m/s)');
xlabel('曲柄转角\theta_1/(\circ))');
xlim([0, 720]);
x_new = linspace(0, 720, 5);
xticks(x_new)
title('速度曲线图');
grid on;

%加速度曲线图
subplot(2,2,3);
yyaxis left;
plot(theta1*du, alpha2);
ylabel('连杆角加速度/rad\cdots^{-2}');
yyaxis right;
plot(theta1*du, a/10^6);
ylabel('滑块加速度/m\cdots^{-1}');
xlabel('曲柄转角\theta_1/(\circ))');
xlim([0, 720]);
x_new = linspace(0, 720, 5);
xticks(x_new)
title('加速度曲线图');
grid on;

%曲柄滑块简图
subplot(2, 2, 4);
x(1) = 0;
y(1) = 0;
x(2) = r * cos(70*hd);
y(2) = r * sin(70*hd);
x(3) = s(70);
y(3) = e;
x(4) = a(70);
y(4) = 0;
x(5) = 0;
y(5) = 0;
x(6) = x(3) - 40;
y(6) = y(3) + 10;
x(7) = x(3) + 40;
y(7) = y(3) + 10;
x(8) = x(3) + 40;
y(8) = y(3) - 10;
x(9) = x(3) - 40;
y(9) = y(3) - 10;
x(10) = x(3) - 40;
y(10) = y(3) + 10;

% 绘制主动杆和连杆
i = 1:3;
plot(x(i), y(i));
grid on;
hold on;
% 绘制机架
i=4:5;
plot(-x(i), y(i));
% 绘制滑块
i= 6:10;
plot(x(i), y(i));
grid on;
hold on;
xlabel('mm');
ylabel('mm');
axis([-50, 400, -20, 130]);
title('曲柄滑块简图');
% 绘制转动副
plot(x(1),y(1),'o');
plot(x(2),y(2),'o');
plot(x(3),y(3),'o');

figure(2);
% 新建avi视频文件
writerObj = VideoWriter('slider');
open(writerObj);
m=moviein(20);
j=0;
for n=1:5:360
    j=j+1;

    clf;
    x(1) = 0;
    y(1) = 0;
    x(2) = r * cos(n*hd);
    y(2) = r * sin(n*hd);
    x(3) = s(n);
    y(3) = e;
    x(4) = (r+l+50);
    y(4) = 0;
    x(5) = 0;
    y(5) = 0;
    x(6) = x(3) - 40;
    y(6) = y(3) + 10;
    x(7) = x(3) + 40;
    y(7) = y(3) + 10;
    x(8) = x(3) + 40;
    y(8) = y(3) - 10;
    x(9) = x(3) - 40;
    y(9) = y(3) - 10;
    x(10) = x(3) - 40;
    y(10) = y(3) + 10;
    % 绘制主动杆和连杆
    i=1:3;
    plot(x(i),y(i));
    grid on;
    hold on;
    % 绘制机架
    i=4:5;
    plot(x(i),y(i));
    % 绘制滑块
    i=6:10;
    plot(x(i),y(i));
    % 绘制转动副
    plot(x(1),y(1),'o');
    plot(x(2),y(2),'o');
    plot(x(3),y(3),'o');
    title('曲柄滑块机构');
    xlabel('mm');
    ylabel('mm');
    axis([-150, 450, -150, 150]);
    m(j)=getframe;
    % 写入视频
    writeVideo(writerObj,m(j));

end
movie(m, 10);
close(writerObj);

function [theta2,s,omega2,v,alpha2,a]=slider_crank(theta1,omega1,alpha1,r,l,e)
    % 计算连杆的角位移和滑块位移
    theta2=asin((e-r * sin(theta1))/l); 
    s=r * cos(theta1) + l * cos(theta2);
    % 计算连杆的角速度和滑块的线速度
    A=[l*sin(theta2), 1; -l*cos(theta2), 0];  % 连杆的位置参数矩阵
    B=[-r*sin(theta1); r*cos(theta1)];    % 主动杆的位置参数矩阵
    
    omega=A \ (omega1*B);   % 连杆的速度矩阵
    omega2=omega(1);
    v=omega(2);
    
    % 计算连杆的角加速度和滑块的线加速度
    Aa=[omega2*l*cos(theta2), 0;
        omega2*l*sin(theta2), 0];  % Aa=dA/dt
    Ba= [-omega1*r*cos(theta1);           
        -omega1*r*sin(theta1)];    % Ba=dB/dt           
    alpha=A \(-Aa*omega+alpha1*B+omega1*Ba);  % 机构从动件的加速度矩阵
    alpha2 = alpha(1);
    a = alpha(2);
end

演示：

基于matlab的曲柄滑块仿真运动