概率论与数理统计期末考试复习总结
为了方便复习下面内容摘自:《高数叔》概率论与数理统计期末总复习笔记(持续更新中)_BitHachi-CSDN博客_高数叔概率论笔记pdf
目录
一、随机时间与概率—day1
1.随机事件与样本空间的概念
2.事件的关系(集合之间的关系)
3.事件的运算律—交换律-结合律-分配律-德摩根律
4.概率的概念和性质
5.古典概型
6.条件概率
7.乘法定理
8.全概率公式
9.贝叶斯公式
10.事件独立性
11.大概会考啥?
12.举几个例子
(1)条件概率与古典概型
(2)德摩根律与古典概型
(3)条件概率
(4)古典概型与组合C
(5)串并联电路与古典概型
(6)古典概型与组合C–正品次品
(7)全概率与贝叶斯公式的应用
(8)贝叶斯公式与全概率公式的应用
练习题—day1
1.德摩根律与条件概率
2.A&B事件判断
3.正品次品组合C- 全概率公式
4.串并联电路
5.零件加工-全概率与贝叶斯公式
二、随机变量及其分布—day2
1.随机变量的概念
2.分布律、分布函数、概率密度
3.常用离散随机变量—(0-1,二项,泊松)分布
4.常用的连续型随机变量分布—(均匀、正态、标准正态、指数)分布
5.举几个例子
(1)求随机变量X的分布律
(2)已知X的分布律,求X的分布函数Fx(X)
(3)求Y=(X-1)2的分布律, Y的分布函数F(Y)
(4)泊松分布X~P(λ)
(5)均匀分布X~U(a,b)
(6)指数分布X~e(λ)
(7)正态分布X~N(μ,σ2)
(8) 已知概率密度f(x),求c的值和X的分布函数F(x)
(9)已知分布函数F(X),求A,B的值及概率密度f(X)X和fY(Y)
(10)已知概率密度f(X)的一道应用题&&二项分布—B(n,p)
练习题—day2
1.古典概型和二项分布—B(n,p)
2.求X的分布律和分布函数F(X)
3.泊松分布X~P(λ)
4.已知X的概率密度函数,y=2x+1,求fy(Y)
5.已知X的分布律,求Y=X2-1的分布律
6.正态分布X~N(μ,σ2)与标准正态分布X~N(0,1)
7.已知概率密度f(x),求a,b和fy(Y)
8.已知概率密度f(X)的一道应用题&&条件概率P(A|B)&&二项分布—B(n,p)
三、二维随机变量及其分布—day3
1.多维随机变量及其分布和独立性
2.二维离散型随机变量的分布及独立性
3.二维连续型随机变量的分布及独立性
4.二维标准正态分布N(0,1)联合概率密度
5.两个随机变量的函数分布
6.举几个例子
(1)已知二维离散型随机向量(X,Y)列表分布律,填完表格。并求u=max{X,Y}分布律、P(X
(2)已知x,y服从N(0,1)分布,求联合概率密度f(X,Y)和Z的分布律
(3)已知二维随机变量的联合分布密度f(X,Y),求X,Y是否相互独立及P(X
(4)已知二维随机变量的联合分布密度f(X,Y),求fx(x)及条件概率fY|X(y|x)
(5)已知X,Y联合密度f(x,y),求P(Y>=X2)和Z=X+Y的概率密度函数
练习题—day3
1.已知X的概率密度函数,A={X>a}与B={Y>a}相互独立,且P(AUB)=3/4,求a的值
2.已知二维随机变量的概率密度函数f(x,y),求边缘密度函数fx(x),fY(y),P(Y>=X2)
3.已知联合概率密度f(x,y),求fz(z),p{min(X,Y)<=1/2}
四、随机变量数字特征—day4
1.数学期望E(X)
2.数学期望的性质
3.方差D(X)与标准差
4.方差的性质
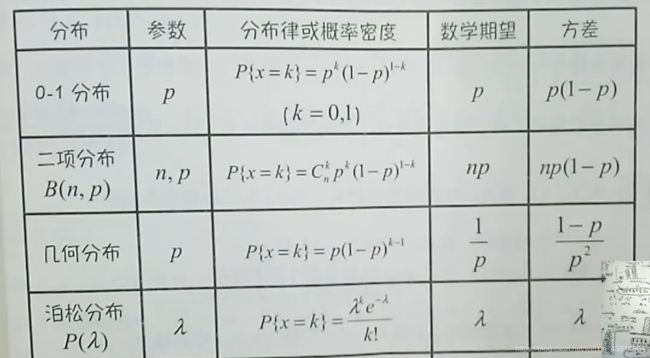
5.常用分布的期望和方差
6.协方差及性质
7.相关系数ρxy
8.矩—原点矩、中心矩
9.举几个例子
(1)泊松分布、指数分布、正态分布,求期望E(X)
(2)均匀分布、泊松分布、正态分布,求期望E(X)、方差D(X)
(3)已知D(X),D(Y),ρxy,求D(X+Y),D(X-Y)
(4)已知(X,Y)联合分布律级边缘分布律,求E(X),E(Y),E(XY),Cov(x,y),ρxy
(5)已知(X,Y),联合分布密度,求E(Z),D(Z)
(6)已知(X,Y),联合分布密度,求边缘密度fx(x),E(Y),E(Y2),D(Y)
练习题—day4
1.泊松分布求λ,正态分布、二项分布、求P,E(U),D(U)
2.已知(x,y)联合分布律表,求协方差Cov(X,Y )
3.已知二维随机变量X,Y)的联合密度函数f(x,y),求D(Y)
五、中心极限定理与抽样分布—day5
1.中心极限定理1、2
2.总体和样本
3.统计量
4.常用统计量
5.常用分布
X2(n)分布
t(n)分布
F分布
正态总体统计量的分布
6.举几个例子
(1)中心极限定理2—B(n,p)
(2)中心极限定理1—N(μ,σ2)
(3)指数分布—e(λ)
(4)常用分布—X2(n)、t(n)、F
(5)正态总体统计分布
练习题—day5
1.常用分布的填空题—X2(n)、t(n)、F
2.中心极限定理1—N(μ,σ2)
3.中心极限定理2—B(n,p)
六、参数估计—day6
1.点估计的概念
2.矩估计法
3.最大似然估计法
4.无偏估计量
5.举几个例子
(1)离散型:矩估计法、最大似然估计求矩估计量
(2)连续型:矩估计法求矩估计量
(3)连续型:最大似然估计法求估计量
(4)连续型:求矩估计量、最大似然估计量
(5)无偏估计
练习题—day6
1.连续型:矩估计法求矩估计量
2.连续型:矩估计法和最大似然估计法求估计量
3.无偏估计
一、随机时间与概率—day1
1.随机事件与样本空间的概念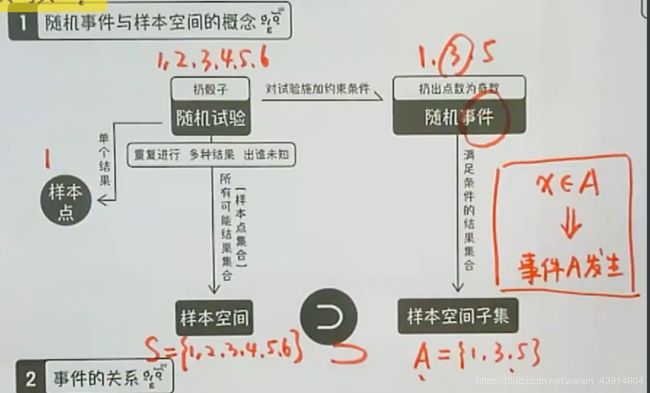
2.事件的关系(集合之间的关系)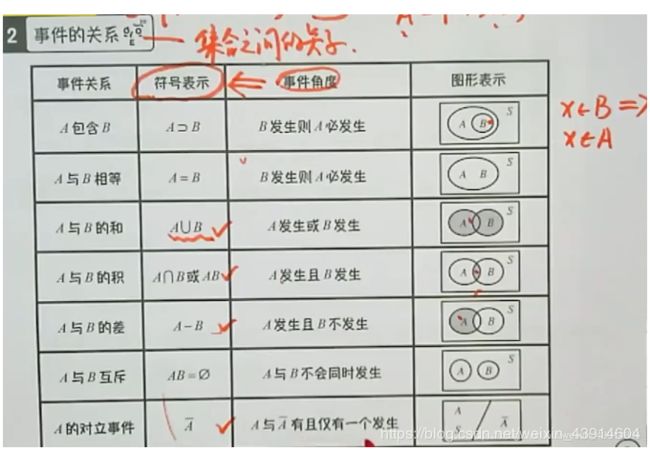
3.事件的运算律—交换律-结合律-分配律-德摩根律
4.概率的概念和性质
5.古典概型
古典概型计算公式
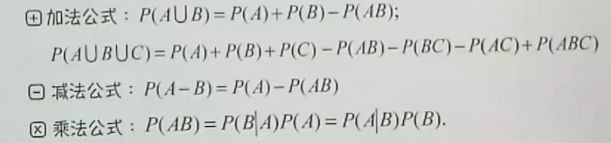
6.条件概率
7.乘法定理
8.全概率公式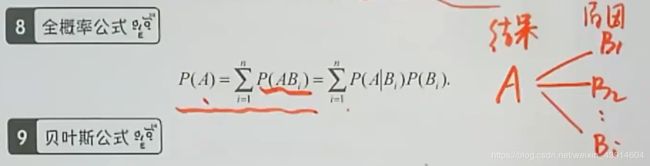
9.贝叶斯公式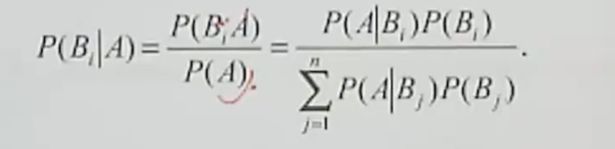
全概率&贝叶斯举例![]()
10.事件独立性
![]()
![]()
11.大概会考啥?
古典概型-加法-减法-乘法公式![]()
12.举几个例子
(1)条件概率与古典概型
(2)德摩根律与古典概型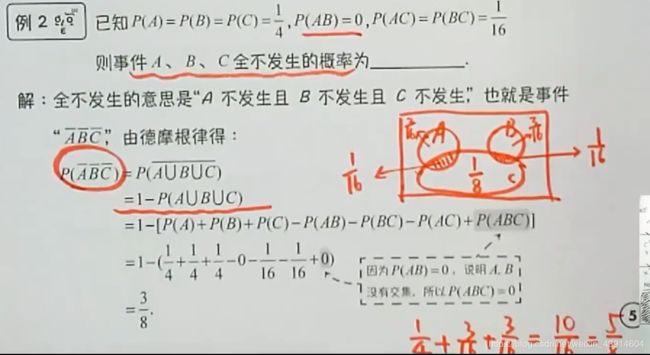
(3)条件概率
(4)古典概型与组合C
![]()
(5)串并联电路与古典概型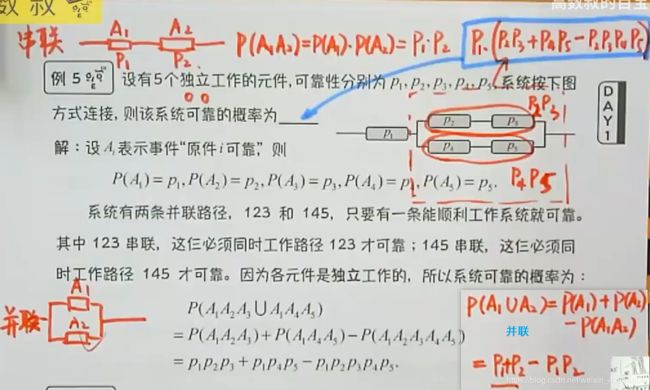
(6)古典概型与组合C–正品次品
![]()
![]()
(7)全概率与贝叶斯公式的应用




(8)贝叶斯公式与全概率公式的应用
![]()
![]()
![]()
依次类推![]()
练习题—day1
1.德摩根律与条件概率 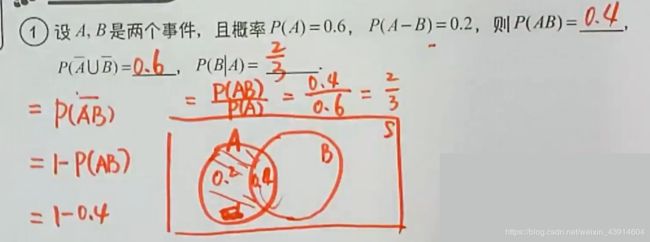
![]()
![]()
2.A&B事件判断 
3.正品次品组合C- 全概率公式 
4.串并联电路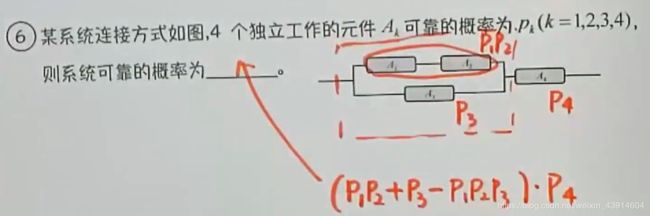
5.零件加工-全概率与贝叶斯公式
![]()
![]()
二、随机变量及其分布—day2
1.随机变量的概念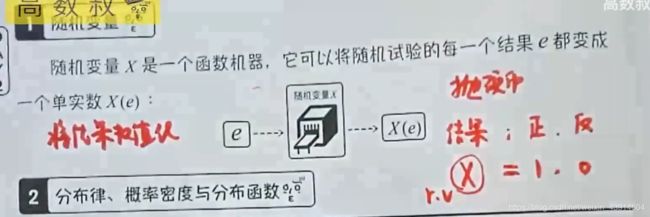
2.分布律、分布函数、概率密度
![]()
3.常用离散随机变量—(0-1,二项,泊松)分布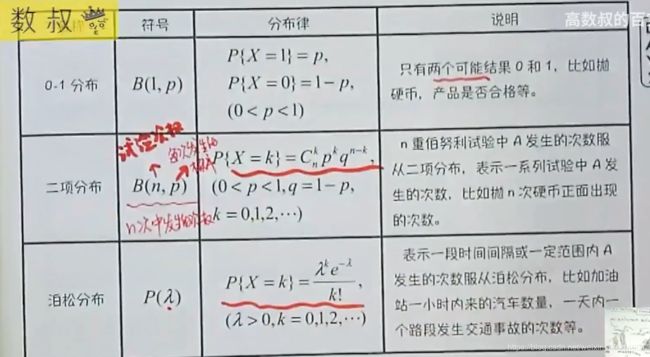
![]()
4.常用的连续型随机变量分布—(均匀、正态、标准正态、指数)分布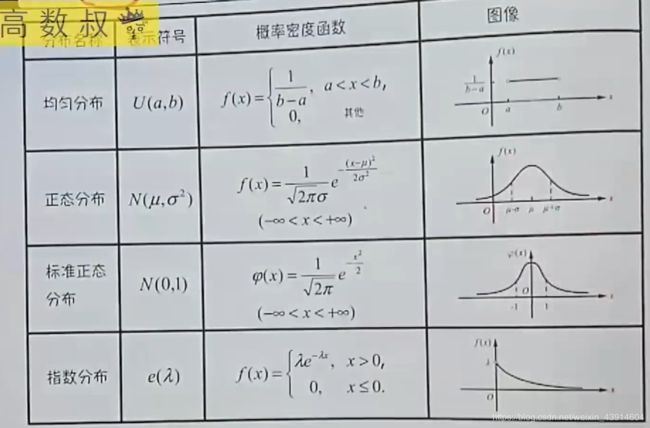
![]()
![]()
![]()
5.举几个例子
(1)求随机变量X的分布律
![]()
第二题:
![]()
(2)已知X的分布律,求X的分布函数Fx(X)
![]()
(3)求Y=(X-1)2的分布律, Y的分布函数F(Y)
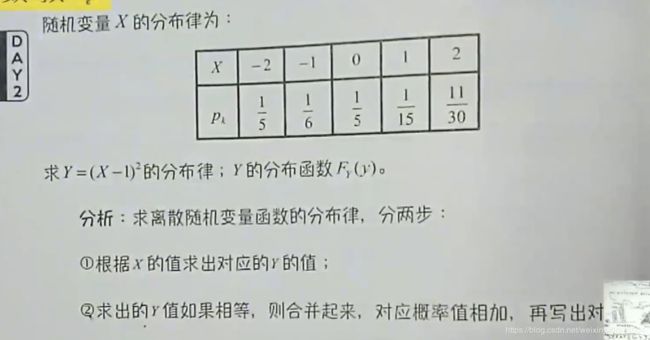
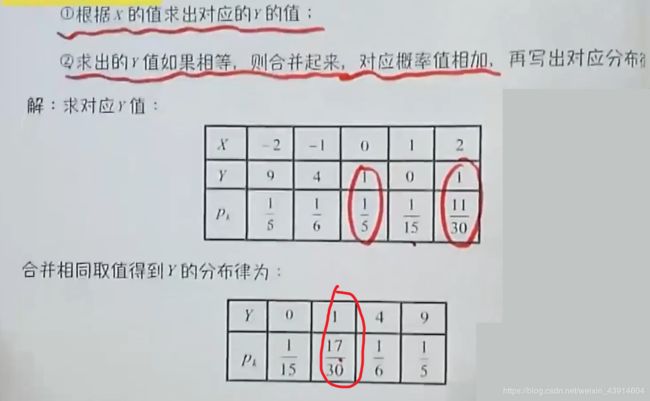

(4)泊松分布X~P(λ)


(5)均匀分布X~U(a,b)
![]()
(6)指数分布X~e(λ)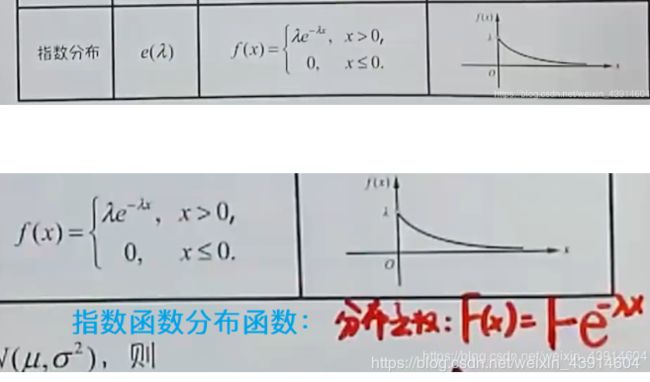
![]()
![]()
(7)正态分布X~N(μ,σ2)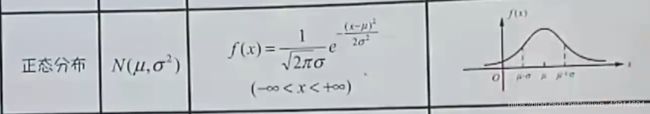
![]()
(8) 已知概率密度f(x),求c的值和X的分布函数F(x)
![]()
![]()
(9)已知分布函数F(X),求A,B的值及概率密度f(X)X和fY(Y)


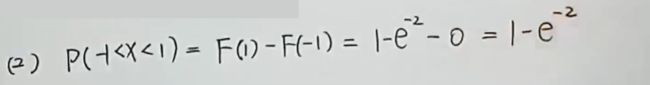

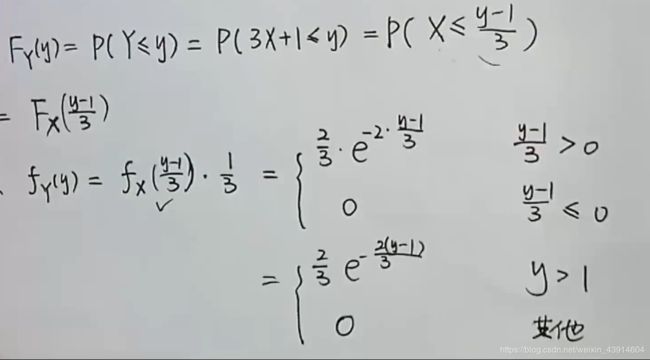
(10)已知概率密度f(X)的一道应用题&&二项分布—B(n,p)
![]()
![]()
![]()
练习题—day2
1.古典概型和二项分布—B(n,p)
![]()
![]()
2.求X的分布律和分布函数F(X)


3.泊松分布X~P(λ)
![]()
4.已知X的概率密度函数,y=2x+1,求fy(Y)
5.已知X的分布律,求Y=X2-1的分布律
6.正态分布X~N(μ,σ2)与标准正态分布X~N(0,1)
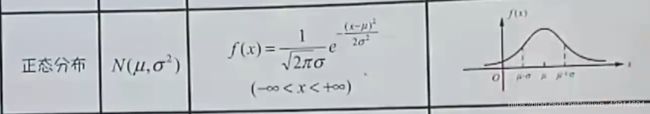

7.已知概率密度f(x),求a,b和fy(Y)
![]()
![]()
![]()
8.已知概率密度f(X)的一道应用题&&条件概率P(A|B)&&二项分布—B(n,p)

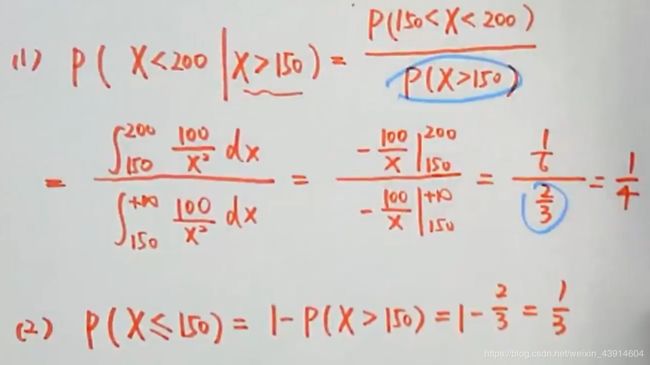

三、二维随机变量及其分布—day3
1.多维随机变量及其分布和独立性
2.二维离散型随机变量的分布及独立性
3.二维连续型随机变量的分布及独立性
![]()
4.二维标准正态分布N(0,1)联合概率密度
5.两个随机变量的函数分布
6.举几个例子
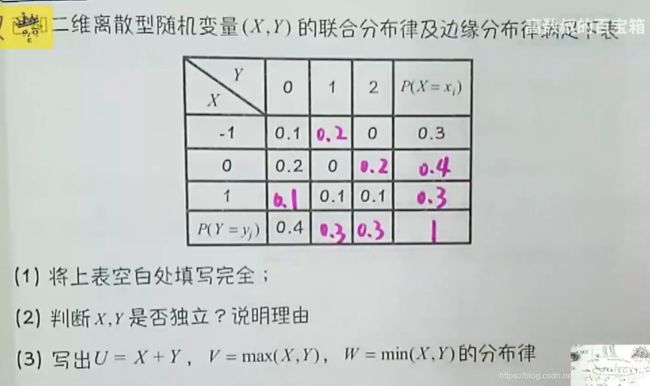
(1)已知二维离散型随机向量(X,Y)列表分布律,填完表格。并求u=max{X,Y}分布律、P(X
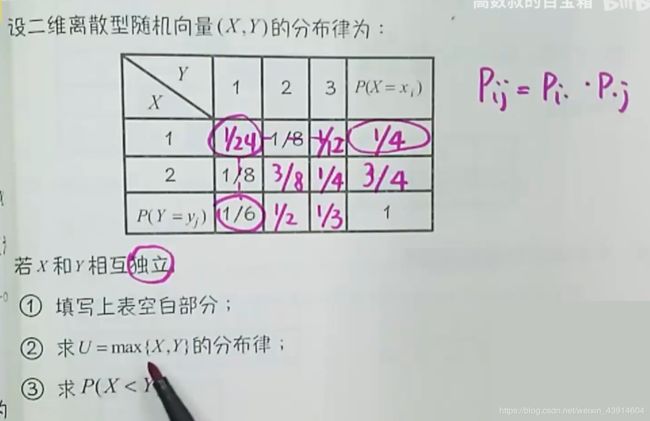

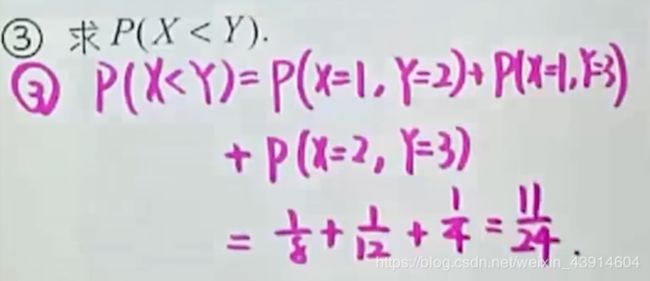
类似的第二题:
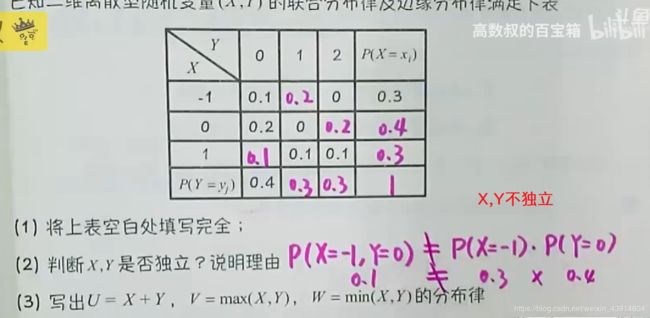



(2)已知x,y服从N(0,1)分布,求联合概率密度f(X,Y)和Z的分布律

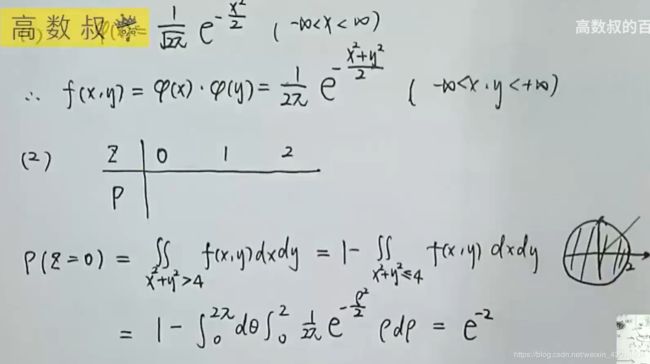
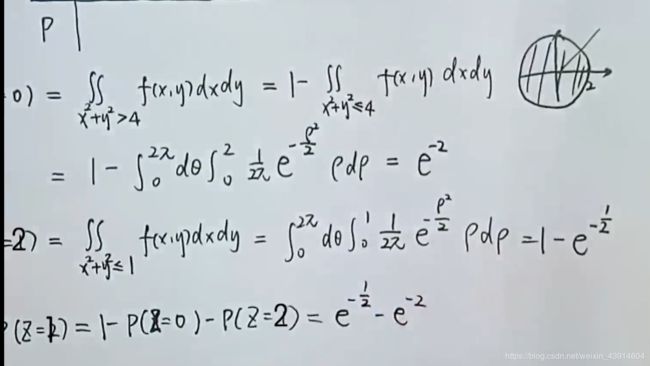
(3)已知二维随机变量的联合分布密度f(X,Y),求X,Y是否相互独立及P(X


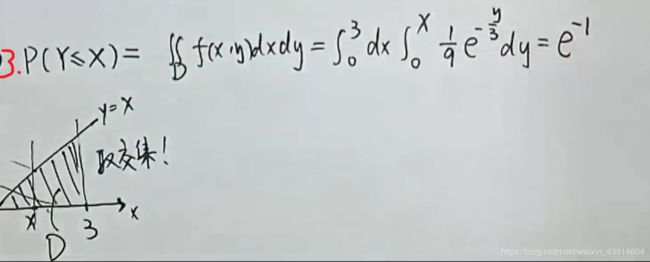
(4)已知二维随机变量的联合分布密度f(X,Y),求fx(x)及条件概率fY|X(y|x)
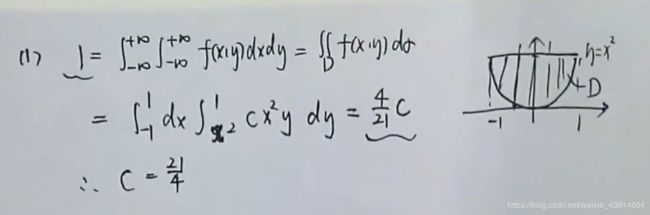



(5)已知X,Y联合密度f(x,y),求P(Y>=X2)和Z=X+Y的概率密度函数
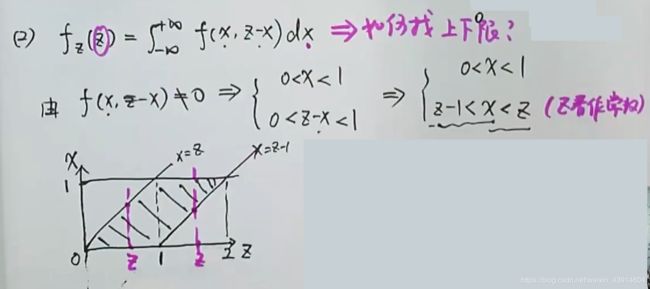
练习题—day3
1.已知X的概率密度函数,A={X>a}与B={Y>a}相互独立,且P(AUB)=3/4,求a的值


2.已知二维随机变量的概率密度函数f(x,y),求边缘密度函数fx(x),fY(y),P(Y>=X2)


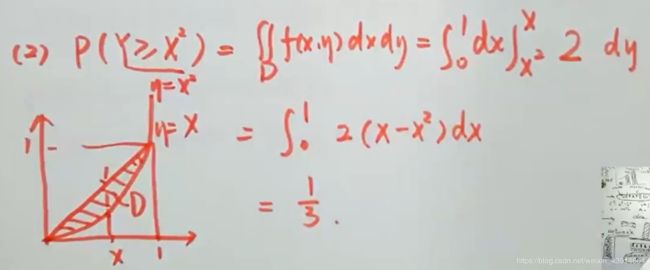
类似的题目:
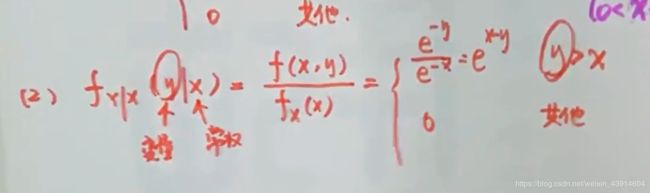
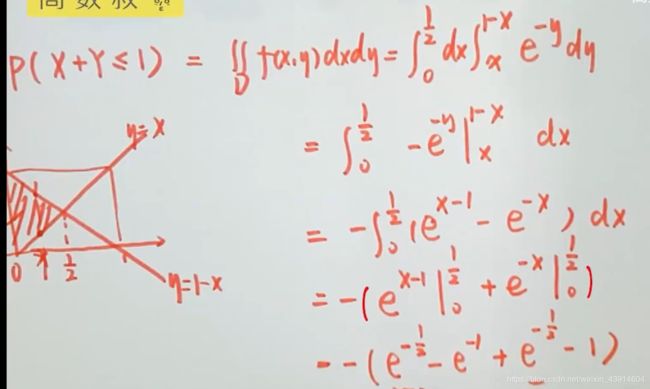
3.已知联合概率密度f(x,y),求fz(z),p{min(X,Y)<=1/2}

可参考前面的例题,关于(2)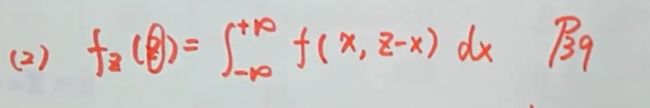

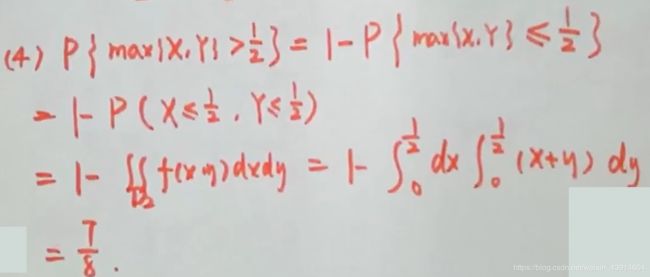
四、随机变量数字特征—day4
1.数学期望E(X)
2.数学期望的性质
3.方差D(X)与标准差
4.方差的性质
5.常用分布的期望和方差

6.协方差及性质

7.相关系数ρxy
8.矩—原点矩、中心矩
9.举几个例子
(1)泊松分布、指数分布、正态分布,求期望E(X)
(2)均匀分布、泊松分布、正态分布,求期望E(X)、方差D(X)

(3)已知D(X),D(Y),ρxy,求D(X+Y),D(X-Y)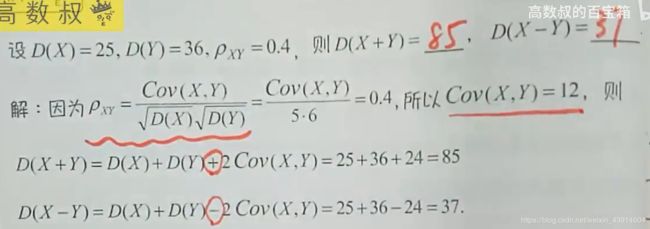
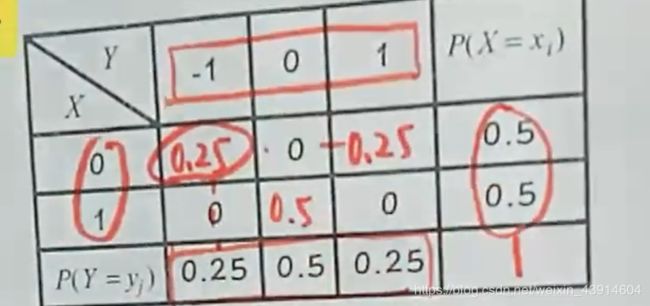
(4)已知(X,Y)联合分布律级边缘分布律,求E(X),E(Y),E(XY),Cov(x,y),ρxy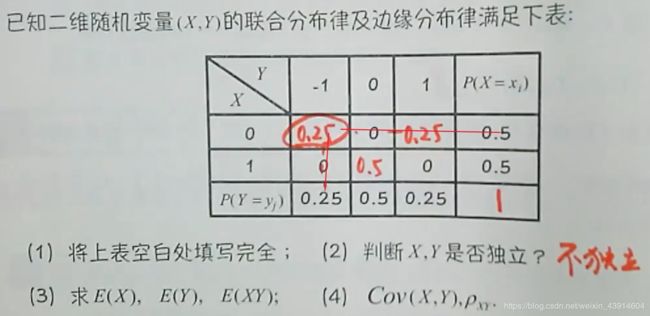


(5)已知(X,Y),联合分布密度,求E(Z),D(Z)


(6)已知(X,Y),联合分布密度,求边缘密度fx(x),E(Y),E(Y2),D(Y)
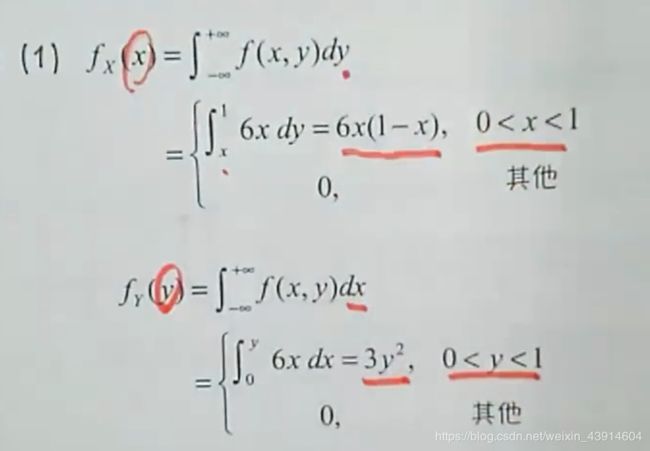

练习题—day4
1.泊松分布求λ,正态分布、二项分布、求P,E(U),D(U)

2.已知(x,y)联合分布律表,求协方差Cov(X,Y )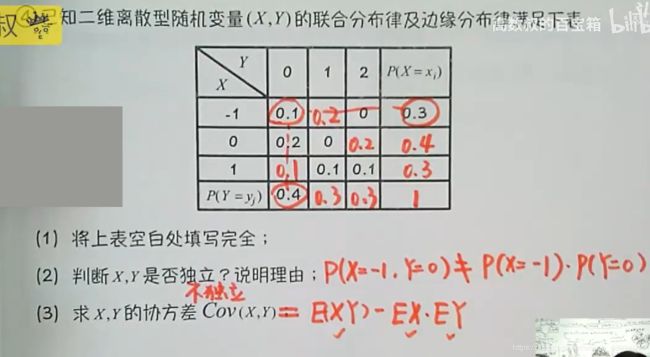

3.已知二维随机变量X,Y)的联合密度函数f(x,y),求D(Y)

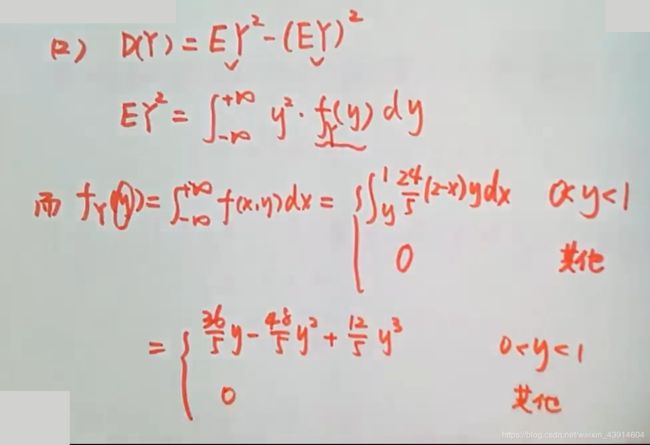

五、中心极限定理与抽样分布—day5
1.中心极限定理1、2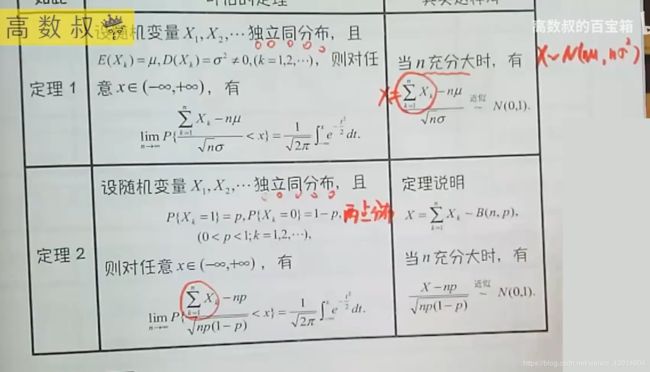
2.总体和样本
3.统计量
4.常用统计量


5.常用分布
X2(n)分布
t(n)分布
F分布
正态总体统计量的分布
6.举几个例子
(1)中心极限定理2—B(n,p)
(2)中心极限定理1—N(μ,σ2)
(3)指数分布—e(λ)
(4)常用分布—X2(n)、t(n)、F
类似第二题:
(5)正态总体统计分布
练习题—day5
1.常用分布的填空题—X2(n)、t(n)、F
********** 重要看个数 **********
2.中心极限定理1—N(μ,σ2)
3.中心极限定理2—B(n,p)
六、参数估计—day6
1.点估计的概念
2.矩估计法
3.最大似然估计法
4.无偏估计量
5.举几个例子
(1)离散型:矩估计法、最大似然估计求矩估计量
类似的第二题,区别在于最大似然估计值求法有点不一样:
(2)连续型:矩估计法求矩估计量
(3)连续型:最大似然估计法求估计量
(4)连续型:求矩估计量、最大似然估计量
(5)无偏估计
练习题—day6
1.连续型:矩估计法求矩估计量
2.连续型:矩估计法和最大似然估计法求估计量
3.无偏估计
![]()
![]()
![]()
类似的第二题:
![]()
![]()
![]()
![]()
![]()
(2)已知x,y服从N(0,1)分布,求联合概率密度f(X,Y)和Z的分布律
![]()
![]()
![]()
(3)已知二维随机变量的联合分布密度f(X,Y),求X,Y是否相互独立及P(X
![]()
![]()
![]()
(4)已知二维随机变量的联合分布密度f(X,Y),求fx(x)及条件概率fY|X(y|x)
![]()
![]()
![]()
![]()
(5)已知X,Y联合密度f(x,y),求P(Y>=X2)和Z=X+Y的概率密度函数
![]()
练习题—day3
1.已知X的概率密度函数,A={X>a}与B={Y>a}相互独立,且P(AUB)=3/4,求a的值


2.已知二维随机变量的概率密度函数f(x,y),求边缘密度函数fx(x),fY(y),P(Y>=X2)
![]()
![]()
![]()
类似的题目:![]()
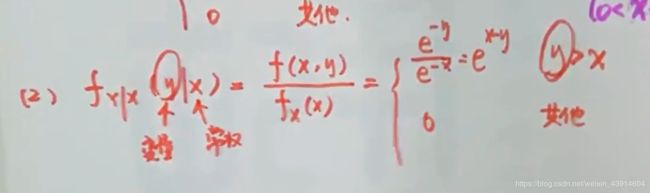
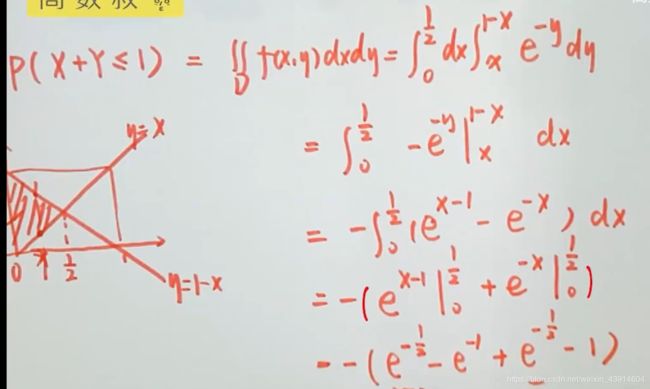
3.已知联合概率密度f(x,y),求fz(z),p{min(X,Y)<=1/2}
![]()
可参考前面的例题,关于(2)![]()
![]()
![]()
四、随机变量数字特征—day4
1.数学期望E(X)
2.数学期望的性质
3.方差D(X)与标准差
4.方差的性质
5.常用分布的期望和方差


6.协方差及性质
![]()
7.相关系数ρxy
8.矩—原点矩、中心矩
9.举几个例子
(1)泊松分布、指数分布、正态分布,求期望E(X)
(2)均匀分布、泊松分布、正态分布,求期望E(X)、方差D(X)
![]()
(3)已知D(X),D(Y),ρxy,求D(X+Y),D(X-Y)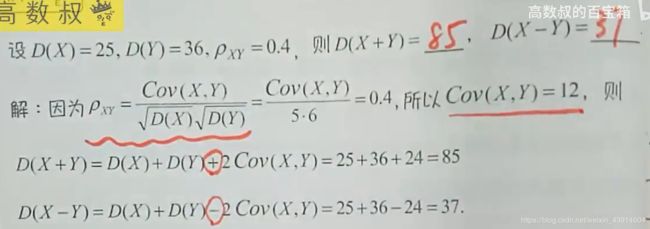
(4)已知(X,Y)联合分布律级边缘分布律,求E(X),E(Y),E(XY),Cov(x,y),ρxy
![]()
![]()
![]()
(5)已知(X,Y),联合分布密度,求E(Z),D(Z)
![]()
![]()
(6)已知(X,Y),联合分布密度,求边缘密度fx(x),E(Y),E(Y2),D(Y)
![]()
![]()
练习题—day4
1.泊松分布求λ,正态分布、二项分布、求P,E(U),D(U)
![]()
2.已知(x,y)联合分布律表,求协方差Cov(X,Y )
![]()
3.已知二维随机变量X,Y)的联合密度函数f(x,y),求D(Y)

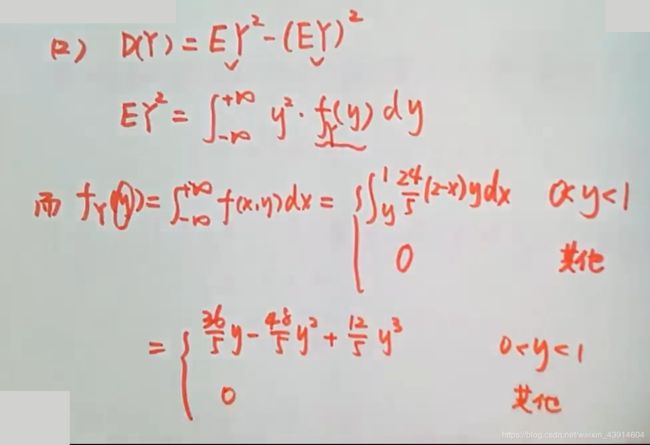

五、中心极限定理与抽样分布—day5
1.中心极限定理1、2
2.总体和样本
3.统计量
4.常用统计量


5.常用分布
X2(n)分布
t(n)分布
F分布
正态总体统计量的分布
6.举几个例子
(1)中心极限定理2—B(n,p)
(2)中心极限定理1—N(μ,σ2)
(3)指数分布—e(λ)
(4)常用分布—X2(n)、t(n)、F
类似第二题:
(5)正态总体统计分布
练习题—day5
1.常用分布的填空题—X2(n)、t(n)、F
********** 重要看个数 **********
2.中心极限定理1—N(μ,σ2)
3.中心极限定理2—B(n,p)
六、参数估计—day6
1.点估计的概念
2.矩估计法
3.最大似然估计法
4.无偏估计量
5.举几个例子
(1)离散型:矩估计法、最大似然估计求矩估计量
类似的第二题,区别在于最大似然估计值求法有点不一样: