理解扩散模型：Diffusion Models & DDPM

引言

在前面的博客中，我们讨论了生成模型VAE和GAN，近年来，新的生成模型——扩散模型受到越来越多的关注，因此值得好好去研究一番。扩散模型（Diffusion Models）最早由 [2] 于2015年提出，但直到2020年论文 [3] 发表之后才得到关注，本文详细梳理了 [3] 中的公式推导部分，帮助大家更好理解其中的数学原理。

---

数学模型

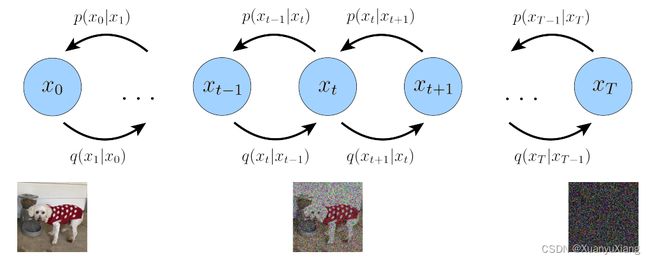
如下图所示（引自[1]），$x_0$ 是原始数据，$q$ 是扩散模型，每扩散一次，都会在前一期数据的基础上添加部分噪声，当 $t\to \infty$，$x_T$ 完全被噪声淹没，成为各向同性的高斯分布 $x_T\sim \mathcal{N}(0,I)$，$p_{\theta }$ 是生成模型，使用参数为 $\theta$ 的网络来近似，将噪声恢复成有效信息，整个模型满足马尔可夫链条件。

目标函数

本文采用自顶向下的形式进行讲解，首先说明最终关注的目标函数，然后针对其中的细节分别深入。直观来说，我们的目标是让近似分布 $p_{\theta }(x_0)$ 尽可能接近数据的真实分布 $q(x_0)$，所以目标函数可以用交叉熵来表示：
$$\begin{array}{rl}{\mathcal{L}}_{CE}& =-{\mathbb{E}}_{q(x_0)}log{p}_{\theta }(x_0)\\ & =-{\mathbb{E}}_{q(x_0)}log[\int p_{\theta }(x_{0:T})d{x}_{1:T}]\\ & =-{\mathbb{E}}_{q(x_0)}log[\int q(x_{1:T}|x_0)\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}d{x}_{1:T}]\\ & =-{\mathbb{E}}_{q(x_0)}log[{\mathbb{E}}_{q(x_{1:T}|x_0)}\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}]\\ & \le -{\mathbb{E}}_{q(x_{0:T})}log\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)},Jenseninequality\end{array}$$
可以得到：
$${\mathbb{E}}_{q(x_0)}log{p}_{\theta }(x_0)\ge {\mathbb{E}}_{q(x_{0:T})}log\frac{p_{\theta }(x_{0:T})}{q(x_{1:T}|x_0)}$$
不等式右边的项就是对数似然下界，记为 ${\mathcal{L}}_{LB}$，只要让其越大，不等式左边的项也就越大，交叉熵也就越小。

马克洛夫链假设

为了让 ${\mathcal{L}}_{LB}$ 便于优化，需要补充一些知识。前面提到，模型满足马克洛夫链条件（Markov Chain），即当前状态 $x_t$ 仅与上一状态 $x_{t-1}$ 有关，假设马克洛夫关系为 $A\to B\to C$，可以得到性质：
$$\begin{array}{rl}p(B,C|A)& =\frac{p(B,C,A)p(A,B)}{p(A)p(A,B)}=p(B|A)p(C|A,B)\\ & =p(B|A)p(C|B)\end{array}\text{\hspace{1em}(1)}$$
利用公式（1），可以得到：
$$\begin{gathered} q(x_{1:T}|x_0)=\prod _{t=1}^{T}q(x_t|x_{t-1}) \\ {p}_{\theta }(x_{0:T})=p_{\theta }(x_T)\prod _{t=1}^T{p}_{\theta }(x_{t-1}|x_t)\text{\hspace{1em}(2)} \end{gathered}$$
将公式（2）代入 ${\mathcal{L}}_{LB}$，可以得到：
$$\begin{array}{rl}{\mathcal{L}}_{LB}& ={\mathbb{E}}_{q(x_{0:T})}[log\frac{q(x_{1:T}|x_0)}{p_{\theta }(x_{0:T})}]\\ & ={\mathbb{E}}_q[log\frac{{\prod }_{t=1}^{T}q(x_t|x_{t-1})}{p_{\theta }(x_T){\prod }_{t=1}^T{p}_{\theta }(x_{t-1}|x_t)}]\\ & ={\mathbb{E}}_q[-log{p}_{\theta }(x_T)+\sum _{t=1}^{T}log\frac{q(x_t|x_{t-1})}{p_{\theta }(x_{t-1}|x_t)}]\\ & ={\mathbb{E}}_q[-log{p}_{\theta }(x_T)+\sum _{t=2}^{T}log\frac{q(x_t|x_{t-1})}{p_{\theta }(x_{t-1}|x_t)}+log\frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}]\\ & ={\mathbb{E}}_q[-log{p}_{\theta }(x_T)+\sum _{t=2}^{T}log\frac{q(x_{t-1}|x_t,x_0)}{p_{\theta }(x_{t-1}|x_t)}\cdot \frac{q(x_t|x_0)}{q(x_{t-1}|x_0)}+log\frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}]\\ & ={\mathbb{E}}_q[-log{p}_{\theta }(x_T)+\sum _{t=2}^{T}log\frac{q(x_{t-1}|x_t,x_0)}{p_{\theta }(x_{t-1}|x_t)}+\sum _{t=2}^{T}log\frac{q(x_t|x_0)}{q(x_{t-1}|x_0)}+log\frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}]\\ & ={\mathbb{E}}_q[-log{p}_{\theta }(x_T)+\sum _{t=2}^{T}log\frac{q(x_{t-1}|x_t,x_0)}{p_{\theta }(x_{t-1}|x_t)}+log\frac{q(x_T|x_0)}{q(x_1|x_0)}+log\frac{q(x_1|x_0)}{p_{\theta }(x_0|x_1)}]\\ & ={\mathbb{E}}_q[log\frac{q(x_T|x_0)}{p_{\theta }(x_T)}+\sum _{t=2}^{T}log\frac{q(x_{t-1}|x_t,x_0)}{p_{\theta }(x_{t-1}|x_t)}-log{p}_{\theta }(x_0|x_1)]\end{array}\text{\hspace{1em}(3)}$$
将公式（3）的最后一行化成 KL 散度的形式：
$$\begin{gathered} {\mathbb{E}}_{q(x_0)}{D}_{KL}[q(x_T|x_0)||p_{\theta }(x_T)]+ \\ {\mathbb{E}}_{q(x_0,x_t)}\sum _{t=2}^T{D}_{KL}[q(x_{t-1}||x_0,x_t)||p_{\theta }(x_{t-1}|x_t)]- \\ {\mathbb{E}}_{q(x_0,x_1)}log{p}_{\theta }(x_0|x_1)\text{\hspace{1em}(4)} \end{gathered}$$
公式（4）第一项对应 VAE 中的正则化损失 $D_{KL}(q_{\varphi }(z|x)||p_{\theta }(z))$，第三项对应于重建损失 ${\mathbb{E}}_{q_{\varphi }(z|x)}[log(p_{\theta }(x|z))]$，第二项是多个 KL 散度的和，每个度量 $p$ 后验分布和 $q$ 已知 $x_0$ 后验分布的距离。

重参数化

利用重参数化技巧可以让公式（4）中的 $x_t$ 可解，进一步简化 ${\mathcal{L}}_{LB}$。给定真实数据 $x_0\sim q(x)$，扩散过程的每一步可以表示为：
$$q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-{\beta }_t}{x}_{t-1},{\beta }_{t}I)\text{\hspace{1em}(5)}$$
其中 ${\beta }_t$ 是一个超参数。利用重参数化技巧，可以使用 $x_0$ 直接计算任意时间点 t 上的 $x_t$，不需要一步步迭代。假设 ${\alpha }_t=1-{\beta }_t,\overline{{\alpha }_t}={\prod }_{i=1}^t{\alpha }_i,{ϵ}_t\sim \mathcal{N}(0,I)$：
$$\begin{array}{rl}{x}_t& =\sqrt{{\alpha }_t}{x}_{t-1}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}\\ & =\sqrt{{\alpha }_t}[\sqrt{{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_{t-1}}{ϵ}_{t-2}]+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-2}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}\\ & =\sqrt{{\alpha }_t{\alpha }_{t-1}}{x}_{t-2}+\sqrt{1-{\alpha }_t{\alpha }_{t-1}}{\overline{ϵ}}_{t-2}\\ & =...\\ & =\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ\\ & \therefore q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{{\overline{\alpha }}_t}{x}_0,(1-{\overline{\alpha }}_t)I)\end{array}\text{\hspace{1em}(6)}$$
其中 $\sqrt{{\alpha }_t-{\alpha }_t{\alpha }_{t-1}}{ϵ}_{t-2}+\sqrt{1-{\alpha }_t}{ϵ}_{t-1}\sim \mathcal{N}(0,1-{\alpha }_t{\alpha }_{t-1})$，从而得到 ${\overline{ϵ}}_{t-2}$。进一步，可以计算 $q(x_{t-1}|x_t,x_0)$ 的解析式：
$$\begin{array}{rl}q(x_{t-1}|x_t,x_0)& =q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)}\\ & \propto exp[-\frac{1}{2}(\frac{(x_t-\sqrt{{\alpha }_t}{x}_{t-1}{)}^2}{{\beta }_t}+\frac{(x_{t-1}-\sqrt{{\overline{\alpha }}_{t-1}}{x}_0{)}^2}{1-{\overline{\alpha }}_{t-1}}-\frac{(x_t-\sqrt{{\overline{\alpha }}_t}{x}_0{)}^2}{1-{\overline{\alpha }}_t})]\\ & =exp[-\frac{1}{2}((\frac{{\alpha }_t}{{\beta }_t}+\frac{1}{1-{\overline{\alpha }}_{t-1}})x_{t-1}^2-(\frac{2\sqrt{{\alpha }_t}}{{\beta }_t}{x}_t+\frac{2\sqrt{{\overline{\alpha }}_{t-1}}}{1-{\overline{\alpha }}_{t-1}}{x}_0)x_{t-1}+C(x_t,x_0))]\end{array}\text{\hspace{1em}(7)}$$
我们知道，$a{x}^2+bx$ 可以化成 $a(x+\frac{b}{2a}{)}^2+c$，那么对于指数项是 $a{x}^2+bx$ 这种格式的高斯分布，$\mu =-\frac{b}{2a},{\sigma }^2=\frac{1}{a}$。设 $q(x_{t-1}|x_t,x_0)=\mathcal{N}(x_{t-1};\tilde{\mu }(x_t,x_0),{\tilde{\beta }}_{t}I)$，代入公式（7）有：
$$\begin{array}{rl}{\tilde{\beta }}_t& =\frac{1-{\overline{\alpha }}_{t-1}}{1-{\overline{\alpha }}_t}\cdot {\beta }_t\\ {\tilde{\mu }}_t(x_t,x_0)& =\frac{\sqrt{{\alpha }_t}(1-{\overline{\alpha }}_{t-1})}{1-{\overline{\alpha }}_t}{x}_t+\frac{\sqrt{{\overline{\alpha }}_{t-1}}{\beta }_t}{1-{\overline{\alpha }}_t}{x}_0\end{array}\text{\hspace{1em}(8)}$$
根据公式（6），将 $x_0=\frac{1}{\sqrt{{\overline{\alpha }}_t}}(x_t-\sqrt{1-{\overline{\alpha }}_t}{ϵ}_t)$ 代入公式（8），可以进一步化简 ${\tilde{\mu }}_t(x_t,x_0)$：
$${\tilde{\mu }}_t(x_t,x_0)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{1-{\alpha }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_t)\text{\hspace{1em}(9)}$$

高斯分布的 KL 散度

重参数化技巧使能够解析计算 $x_t$ 和 $q(x_{t-1}|x_t,x_0)$，除此之外，当前分布为高斯分布时，KL 散度的计算也能得到简化，考虑一维高斯分布 $a\sim \mathcal{N}({\mu }_1,{\sigma }_1^2),b\sim \mathcal{N}({\mu }_2,{\sigma }_2^2)$，它们的 KL 散度为（同理可以扩展到多维高斯分布）：
$$\begin{array}{rl}{D}_{KL}(a||b)& ={\mathbb{E}}_{a}log\frac{a}{b}\\ & ={\mathbb{E}}_a[log\frac{{\sigma }_2}{{\sigma }_1}+\frac{(x-{\mu }_2{)}^2}{2{\sigma }_2^2}+\frac{(x-{\mu }_1{)}^2}{2{\sigma }_1^2}]\\ & =log\frac{{\sigma }_2}{{\sigma }_1}+\frac{1}{2}{\mathbb{E}}_a[\frac{(x-{\mu }_2{)}^2}{{\sigma }_2^2}+\frac{(x-{\mu }_1{)}^2}{{\sigma }_1^2}]\\ & =log\frac{{\sigma }_2}{{\sigma }_1}+\frac{1}{2}{\mathbb{E}}_a[(\frac{1}{{\sigma }_2^2}-\frac{1}{{\sigma }_1^2})x^2+(\frac{2{\mu }_1}{{\sigma }_1^2}-\frac{2{\mu }_2}{{\sigma }_2^2})x+\frac{{\mu }_2^2}{{\sigma }_2^2}-\frac{{\mu }_1^2}{{\sigma }_1^2}]\\ & =log\frac{{\sigma }_2}{{\sigma }_1}+\frac{{\sigma }_1^2+({\mu }_1-{\mu }_2{)}^2}{2{\sigma }_2^2}-\frac{1}{2}\end{array}\text{\hspace{1em}(10)}$$

优化目标函数

公式（4）中的第一项是常数，第三项可以看作是第二项 $t=1$ 时的结果，所以我们主要考虑第二项。设 $p_{\theta }(x_{t-1}|x_t)=\mathcal{N}(x_{t-1};{\mu }_{\theta }(x_t,t),{\sigma }_t^{2}I)$，根据公式（10），第二项可以化简为：
$$L_{t-1}={\mathbb{E}}_q[\frac{1}{2{\sigma }_t^2}||{\tilde{\mu }}_t(x_t,x_0)-{\mu }_{\theta }(x_t,t)|{|}^2]+C\text{\hspace{1em}(11)}$$
将公式（9）代入公式（11）可以得到：
$$L_{t-1}={\mathbb{E}}_{x_t,ϵ}[\frac{1}{2{\sigma }_t^2}||\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}ϵ)-{\mu }_{\theta }(x_t,t)|{|}^2]\text{\hspace{1em}(12)}$$
[3]作者进行了参数化 ${\mu }_{\theta }(x_t,t)=\frac{1}{\sqrt{{\alpha }_t}}(x_t-\frac{{\beta }_t}{\sqrt{1-{\overline{\alpha }}_t}}{ϵ}_{\theta }(x_t,t))$，相当于网络拟合的是每个时间点的噪声（为什么选择这样参数化我还没明白），同时代入公式（6），公式（12）进一步化简为：
$$L_{t-1}={\mathbb{E}}_{x_0,ϵ}[\frac{{\beta }_t^2}{2{\sigma }_t^2{\alpha }_t(1-{\overline{\alpha }}_t)}||ϵ-{ϵ}_{\theta }(\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t)|{|}^2]$$
[3]作者发现，将前面的系数丢掉，训练更加稳定，因此得到最终的损失：
$$L_{simple}={\mathbb{E}}_{t,x_0,ϵ}[||ϵ-{ϵ}_{\theta }(\sqrt{{\overline{\alpha }}_t}{x}_0+\sqrt{1-{\overline{\alpha }}_t}ϵ,t)|{|}^2]$$

参考

[1] Understanding Diffusion Models: A Unified Perspective
[2] Deep Unsupervised Learning using Nonequilibrium Thermodynamics
[3] Denoising Diffusion Probabilistic Models
[4] What are Diffusion Models?
[5] Probabilistic Diffusion Model概率扩散模型理论