动手学深度学习v2笔记-Day5-模型选择&权重衰退

动手学深度学习v2

Day 5

---

0x00 模型选择

1.训练误差&泛化误差（更关心）

类别	释义
训练误差	模型在训练数据集上的误差
泛化误差	模型在新的数据集上的误差

2.验证数据集&测试数据集

类别	释义
训练数据集	训练模型的数据集
验证数据集	用来评估模型好坏的数据集（例如50%的训练数据集）
测试数据集	只使用一次的数据集

验证数据集可以用来验证超参数的选择是否合适

3.K折交叉验证
没有足够的数据可以使用（常态），常取K为5或10

将训练数据集分割为k块
第i次使用第i块作为验证数据集，剩余k-1块作为训练数据集
最终取k个验证集的误差平均作为结果

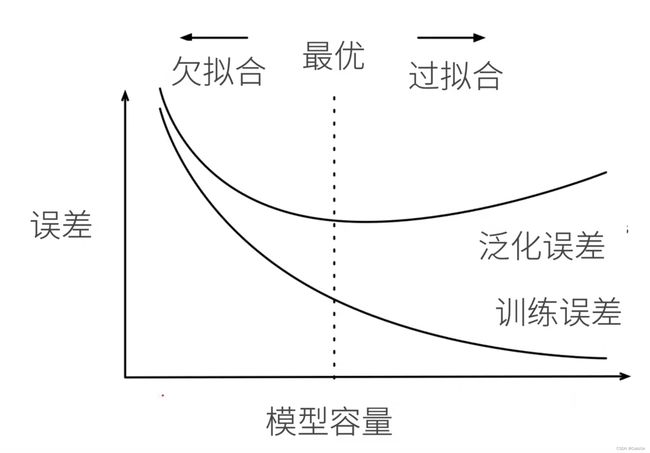
0x01 欠拟合&过拟合

1.模型容量
拟合各种函数的能力
低容量难以记住所有训练数据，高容量可以记住全部数据（包括噪声）

模型容量需要匹配数据复杂度
实际应用中一般还是观察训练误差和验证误差的区别

0x02 权重衰退

最常见的处理过拟合的方法
最广泛使用的正则化技术之一

1.控制模型容量的两种方法
a.将模型的参数数量变小
b.将模型的每个参数的可变范围变小（权重衰退）

• 硬性限制
  做法：最小的损失函数$ l(w,b) $ 加入硬性限制使得$||w|{|}^2\le \theta$
  一般不限制$b$
  小的$\theta$意味着对值的限制更强（显然）

• 柔性限制
  对于每个$\theta$，都可以找到一个$\lambda$使得之前的目标函数等价于
  $$minl(w,b)+\frac{\lambda }{2}||w|{|}^2$$
  $\lambda$是一个超参数，控制正则项的大小
  通俗解释：将之前的硬性控制小于$\theta$，改为对于原始的损失函数加入一项$\frac{\lambda }{2}||w|{|}^2$

2.为什么叫权重衰退
计算梯度：
$$\frac{\partial }{\partial w}[l(w,b)+\frac{\lambda }{2}||w|{|}^2]=\frac{\partial l(w,b)}{\partial w}+\lambda w$$
在时间t的时候更新参数：
$$w_{t+1}=(1-\eta \lambda )w_t-\eta \frac{\partial l(w_t,b_t)}{\partial w_t}$$
通常在更新的时候$\eta \lambda <1$，因此这个权重更新可以看出会变小，因此叫权重衰退

3.代码实现
根据以下公式生成一些数据
$$y=0.05+\sum _{i=1}^{d}0.01x_i+cc\sim N(0,0.01)$$

# 生成数据
# 还是线性回归问题，这里训练集20个远小于测试集是为了更有利于过拟合
n_train, n_test, num_inputs, batch_size = 20, 100, 200, 5
true_w, true_b = torch.ones((num_inputs, 1)) * 0.01, 0.05
train_data = d2l.synthetic_data(true_w, true_b, n_train)
train_iter = d2l.load_array(train_data, batch_size)
test_data = d2l.synthetic_data(true_w, true_b, n_test)
test_iter = d2l.load_array(test_data, batch_size, is_train=False)

初始化模型参数

def init_params():
    w = torch.normal(0, 1, size=(num_inputs, 1), requires_grad=True)
    b = torch.zeros(1, requires_grad=True)
    return [w, b]

这一节最重要的内容，定义L2正则范数

def l2_penalty(w):
    return torch.sum(w.pow(2)) / 2

训练过程

def train(lambd):
    w, b = init_params()
    net, loss = lambda X: d2l.linreg(X, w, b), d2l.squared_loss
    num_epochs, lr = 100, 0.003
    animator = d2l.Animator(xlabel='epochs', ylabel='loss', yscale='log',
                            xlim=[5, num_epochs], legend=['train', 'test'])
    for epoch in range(num_epochs):
        for X, y in train_iter:
            l = loss(net(X), y) + lambd * l2_penalty(w)  # 加入了范数损失
            l.sum().backward()
            d2l.sgd([w, b], lr, batch_size)
        if (epoch + 1) % 5 == 0:
            animator.add(epoch + 1, (d2l.evaluate_loss(net, train_iter, loss),
                                     d2l.evaluate_loss(net, test_iter, loss)))
    print('w的L2范数是：', torch.norm(w).item())


# 开始训练
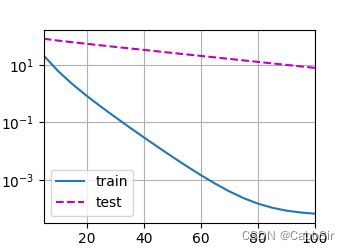
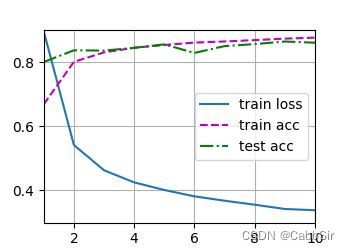
train(0)
d2l.plt.show()
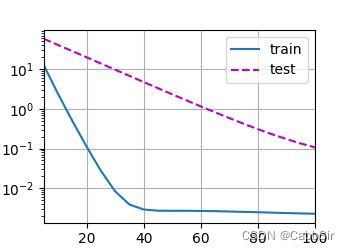
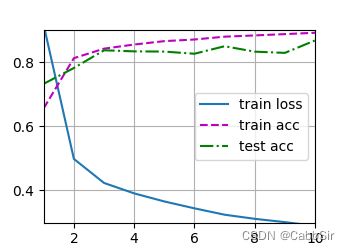
train(3)
d2l.plt.show()
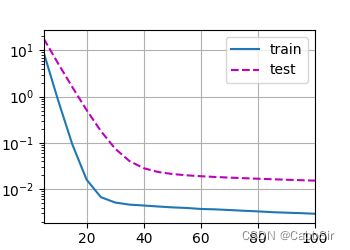
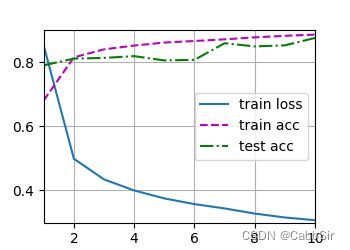
train(10)
d2l.plt.show()

可以比较下这三种情况的不同输出看一看lambda对于过拟合的修正效果

• $\lambda =0$
  

• $\lambda =3$
  

• $\lambda =10$
  

0x03 丢弃法（dropout）

1.动机
一个好的模型需要对于输入数据中的噪声鲁棒

• 使用带有噪声的数据等价于Tikhonov正则
• 丢弃法 --> 在层间加入噪声
• 丢弃法事实上是一种正则

2.无偏差的加入噪声
加入噪声之后，不改变源数据的期望，即：
$$E[x^{\prime }]=x$$
丢弃法对每个元素做以下操作：
$$x_i^{\prime }=\{\begin{array}{ll}0& (p)\\ \frac{x_i}{1-p}& (非p)\end{array}$$
概率$P$（超参数）内x变为0，p概率外将数字变大，保证处理后数据期望不变
将一些输出项随机置0，来控制模型复杂度

3.使用
通常将dropout层作用于隐藏全连接层的输出上，很少用在CNN等上

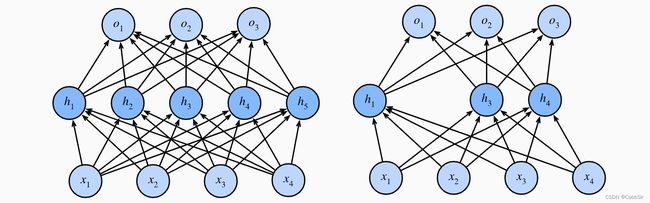
可以看到dropout后隐藏层中的单元少了（被处理为0了）

dropout只在训练中使用，因为他是个正则项，会影响模型参数的更新
在预测过程中，全部参数不需要更新的情况下不使用dropout
因此，在推理（预测）过程中，dropout原样返回输出：
$$h=dropout(h)$$
效果可能比上述权重衰减使用的L2正则项好一点

4.代码

import torch
from torch import nn
from d2l import torch as d2l


def dropout_layer(X, dropout):  # 那其实dropout这个变量就是那个概率P
    assert 0 <= dropout <= 1
    if dropout == 1:  # 全丢弃
        return torch.zeros_like(X)
    if dropout == 0:  # 全保留
        return X
    mask = (torch.rand(X.shape) > dropout).float()  # 随机选取元素为0，巧妙
    return mask * X / (1.0 - dropout)  # 做乘法比选择元素快


X = torch.arange(16, dtype=torch.float32).reshape((2, 8))

# 使用双隐藏层，每个隐藏层后面加一个dropout层
num_inputs, num_outputs, num_hiddens1, num_hiddens2 = 784, 10, 256, 256

dropout1, dropout2 = 0.2, 0.5


class Net(nn.Module):
    def __init__(self, num_inputs, num_outputs, num_hiddens1, num_hiddens2,
                 is_training=True):
        super(Net, self).__init__()
        self.num_inputs = num_inputs
        self.training = is_training
        self.lin1 = nn.Linear(num_inputs, num_hiddens1)
        self.lin2 = nn.Linear(num_hiddens1, num_hiddens2)
        self.lin3 = nn.Linear(num_hiddens2, num_outputs)
        self.relu = nn.ReLU()

    def forward(self, X):
        H1 = self.relu(self.lin1(X.reshape((-1, self.num_inputs))))

        if self.training == True:  # 只有在训练模型时才使用dropout
            H1 = dropout_layer(H1, dropout1)  # 在第一个全连接层之后添加一个dropout层
        H2 = self.relu(self.lin2(H1))
        if self.training == True:
            H2 = dropout_layer(H2, dropout2)  # 在第二个全连接层之后添加一个dropout层
        out = self.lin3(H2)  # 输出不做dropout
        return out


net = Net(num_inputs, num_outputs, num_hiddens1, num_hiddens2)

num_epochs, lr, batch_size = 10, 0.5, 256
loss = nn.CrossEntropyLoss(reduction='none')
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
trainer = torch.optim.SGD(net.parameters(), lr=lr)
d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)

下面是四次不同的dropout概率实验

• dropout1, dropout2 = 0.2, 0.5
  

• dropout1, dropout2 = 0.0, 0.0
  

• dropout1, dropout2 = 0.2, 0.0
  

• dropout1, dropout2 = 0.0, 0.5